“营改增”、税赋降低与企业生产率提升
杨扬,李子越
(中山大学 国际金融学院,广东 珠海 519082)
中国增值税的历史可追溯至1979年首次试行的“营改增”政策,并在1984年确立了“双轨并行”的营业税与增值税同时实行的税制。中国实行的复税制体系,在新中国成立以来的经济发展中,有力地促进了中国经济的发展,但也存在着诸多问题,如间接税比重高、企业税负重,并由此造成国内商品市场流动壁垒与商品价格高企等问题,对于消费、外贸、经济转型升级都产生了不利的影响,税收体制亟需改革。中国自2012年1月1日起开始了营业税改征增值税的改革试点,示范地点与行业是上海的交通运输业与部分现代服务业,并在此基础上一步步扩大范围,于2016年5月1日起,在全国各行业全面推行增值税,营业税开始告别历史舞台。魏陆发现,根据目前的政策实施效果,“营改增”的减税效应明显,绝大多数行业和企业的税收负担是下降的,对产业发展的联动效应也有所凸显[1]。由此可以看出,自2012年逐步推进的“营改增”税制改革,对减轻企业税赋、促进企业研发创新和产业链培育方面产生了积极效果。
在“营改增”的减税效应中,大部分行业产业链减税明显,消除重复征税。相对于营业税,增值税不仅消除了企业的重复征税问题,还通过服务企业下游增值纳税人由取得营业税发票不能抵扣变为取得增值税发票可以抵扣,从而在产业链层面避免了重复征税问题。尽管此次增值税改革涉及行业仅包括服务业,但其作用仍然可以向外延伸至实体制造业。产业链带来的减负效果是广泛的,全面实施“营改增”后,下游企业由不能抵扣改为可抵扣,从而减轻来自产业链的税负,由于产业链税负受到下游企业是否可开具增值税专用发票的影响,生产性服务业减负要大于生活性服务业。但亦有研究表明,有一部分的企业纳税增加,出现了“水涨而船未高”的情形,其主要原因则在于价格管制与税率设置不当[2]。童锦治等从税负转移出发,发现不同企业的议价能力将影响“营改增”对企业实际流转税税负的降低作用[3]。
在对企业研发创新的激励中,“营改增”前,服务企业由于缴纳增值税,外购设备与不动产缴纳税额不准许抵扣;“营改增”后,服务业征收增值税,外购设备与不动产包含在外购材料、服务所发生的进项中,允许抵扣。这使得外购设备成本大大降低,可以对企业加快设备更新和商业不动产购置产生较大的激励效应;结余资金也可以用于设备的更新与研发,进而激发微观主体活力与创造力。谭光荣等利用双重差分倾向匹配得分法发现“营改增”政策促进了服务型制造业企业增加研发投入,且对不同规模的制造业上市公司的研发投入影响差异不大[4]。但也有曹平等学者提出,“营改增”政策显著抑制了服务业企业的技术创新意愿,由于企业税负减轻带来的生存状况的改善,企业对技术进步和提高生产率可能缺乏足够的动力和热情[5]。
在对产业链培育及专业化分工水平的影响中,“营改增”的全面实施,拉长了产业链并提高了服务业的专业化分工水平。以东方传媒为例,过去由于营业税的重复征收制约了集团公司制作和播出;“营改增”后,公司根据增值税的抵扣制度特点推进节目制作与播出改制,成立了一批节目制作、技术服务公司,拓展对外服务,年均增长20%以上。因此,“营改增”在培育产业链和促进企业分工的同时,也涵养了税源,促进了国民经济的良性健康发展。根据钱晓东的研究,“营改增”对一体化程度越高,企业的研发激励就越强,且在非国有企业影响显著,在国有企业则无显著影响[6]。
“营改增”从7年前的试点实施至今,已取得了税制完善优化、企业减轻负担、产业转型优化等一系列积极影响,成为中国经济转型深化的巨大亮点,学界也对此展开了相关研究。为研究其对居民福利和经济整体运行的影响,胡怡建等使用投入产出法与CGE模型相结合,测算了各行业“营改增”对中国宏观经济、产业结构与居民收入分配的影响。通过实证研究发现,“营改增”会使居民名义收入增长1.67%,但就业水平降低1.70%;在产业结构层面,工业促进作用大于服务业;就居民收入分配状况而言,城镇居民收入分配差距拉大,但农村居民收入分配差距缩小[7]。
在“营改增”对分工效应的影响上,陈钊等利用2008~2014年中国上市公司的数据并使用双重差分的方法检验了企业经营范围的变化与营业收入的变化,表明制造业企业开始更多地将业务外包,税制改革促进了企业的专业化分工[8]。范子英等基于135个行业的投入产出表测算了产业互联程度,并使用三重差分法(DDD)评估“营改增”这一税制改革对企业减税和分工的影响,研究认为,“营改增”企业的平均税负没有出现明显的下降,但是在产业互联水平较高的企业当中产生了明显的减税效应与分工效应[9]。
在“营改增”对分工效应、企业行为和企业绩效的影响上,李成等利用2011~2013年企业微观数据,通过双重差分模型检验“营改增”的政策效果,发现企业人均销售额显著增加,企业全要素生产率显著提升,且行业差距明显[10]。周密基于中国上市企业对企业的研发投入进行实证研究,通过双重差分固定效应方法,发现“营改增”显著激励了企业的研发投入,随着时间的推移,这一效应逐渐增强,且存在企业异质性[11]。
我们总结以往的相关研究发现,在宏观层面,既有文献主要考察税制改革对产业结构调整与专业分工的影响;在微观层面,已有主要关注“营改增”政策对企业经营范围与业绩绩效等所带来的影响。而在对企业全要素生产率的讨论上,还鲜有文献探讨“营改增”、税收负担与全要素生产率三者之间的关联及其影响机制。总体而言,现有的相关研究还存在以下改进空间:其一,目前针对“营改增”的讨论大多为实证研究,还需补充相应的理论模型给予说明;其二,大部分学者对全要素生产率影响因素的研究仍注重于资本质量、人力资源、技术水平等方面,对宏观税收政策与企业全要素生产率之间关联及其传导机制的研究仍然有待补充;其三,“营改增”从开始试点到全行业实施历经4年,成果的显现需要时间,早期的文献由于数据不完善及改革成效尚未凸显等原因,导致最后的实证结果可能存在偏误,还需要最新的数据进行验证。
因此,为探究“营改增”政策对企业全要素生产率的影响及其机制,本文建立理论模型,并提出假说,认为“营改增”改革减轻了中国企业税收负担,且通过促进企业研发与产业链专业化分工的途径提高了中国企业的全要素生产率。本文基于中国上市公司数据,通过实证回归证实了理论假说,并进行稳健性检验和企业异质性分析。本文的研究为全面了解“营改增”对企业生产率的作用机制提供了较为详细的分析,为评估“营改增”的成果提供了事实依据,并为推进其他相关的税制改革提供有益的参考。
一、理论模型与假说提出
增值税与营业税在实际征收方面存在显著差异。增值税可以进项抵扣,其实际税负与生产环节无关;营业税会经由生产环节逐步叠加,生产环节越多,实际税负越重。下面将通过计算产品实际税负率的方法比较两税种征收对企业税负的影响。
假设生产环节为n,第i个生产环节的价格为Pi,第n个生产环节的价格为Pn,第i个环节的增加值为vi,第i个环节产品的增值税率和营业税率分别为tv和tb,则
(1)
增值税是价外税,进入进项抵扣账户核算,不计入生产成本,因此实际的税负率等于增值税率
Tv=tv
(2)
营业税是价内税,会随着生产原料计入本环节的生产成本有重复征收问题,此时的征税价格Pn为
(3)
为方便讨论,不妨令各环节增值率为Δ,x为本环节增加值与征税价格之比
(4)
(5)
在第n个生产环节时征收营业税,各自对应的增加值与产品价格分别为
vn=v0(1+x)n-1(1+tb)nx
(6)
Pn=v0(1+x)n(1+tb)n
(7)
在第n个生产环节不征税价格Pn'为

(1+x)n(1+tb)n]/[1-(1+x)(1+tb)]-1=
v0×[tb+x(1+x)n(1+tb)n+1]/[x+tb+xtb]
(8)
两者相除,即可得到产品营业税征收时的实际税负率Tb
(9)
式中:若生产环节足够多,对n取极限
(10)
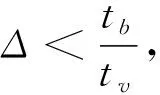
由此可以提出本文的假说1: “营改增”后企业的实际税负的变化与增值税抵扣链条的完整度有关。
接下来对“营改增”所带来的其他微观效应进行探讨。假设企业的生产决策分为两个步骤:(1)选择研发密度;(2)进行产量竞争。与此对应,企业的生产成本也可以分别看作两部分:研发成本Cu与生产成本Cd。以Q代表产量,以c代表成本系数,以P代表产品价格,可以得到
(11)
在支付研发成本与生产成本后,企业的利润π为
(12)
式中:a、b、c分别为需求函数的系数。研发投入z提高与专业化分工v都会带来生产效率的提高,进而提高产量
(13)
式中:假设研发x的增长对产量Q的增加是线性的,分别设定为k、h,P为价格,e是需求弹性。
(14)
(15)
式中:LI即“勒拿指数”,MR代表边际收益,MC代表边际成本,e代表需求弹性,α为求偏导,根据式(12),π的函数形式使π与Q、x相关,根据链式法则:
(16)
“营改增”税制改革后,研发费用可抵扣,δx为实际承担的研发费用,δ代表抵扣程度,0<δ<1。
对研发进行求导,得到新的一阶条件
(17)
企业在研发投入方面得到了一个新的均衡点,企业可以通过提高研发投入获得更多的消费者剩余,提高企业获益。同时企业也会受益于“营改增”带来的专业化分工提升,边际成本会下降
(18)
此时,在价格不变的条件下,产品产量提高,勒拿指数降低,边际成本曲线右移,企业获得的生产者剩余增加,以此提高企业利润。
为了进一步探究“营改增”所引起的研发投入提升与专业化分工延伸,借鉴Melitz[12]的生产成本假设对生产成本C作出如下规定
(19)
对个体企业而言,固定成本f>0,φ代表了不同的生产率水平,生产率越高,即可以在相同的生产成本条件下生产更多的产品。根据先前的推导,研发投入的增加与专业化水平的提高都会带来边际生产成本的降低,即
(20)
全要素生产率A与生产成本成反比,生产成本与研究投入、分工水平负相关,因此,可以自然地推导出
A∝x,A∝v
(21)
由此可以提出另外两个重要假说,即
假说2:“营改增”后,研发支出可进行税收抵扣,企业提高研发投入,进而全要素生产率也将提高。
假设3:“营改增”后,企业的分工水平提升,全要素生产率随着专业化水平的上升而提高。
二、计量模型、数据和变量
(一)计量模型
本文的目的是评估“营改增”政策所带来的生产效率改进,以及是否通过提高企业研发投入与专业化分工水平两种途径影响企业生产率,采用的方法是政策评估中的双重差分法(DID法)。在本文研究中,作为对照组的是未进行试点的地区和行业,由于“营改增”政策是分地区分行业逐步推广,试点行业是同时在地区和时间两个层面上发生变化,可以通过DID方法差分得到“营改增”的净效应。
依据前文的模型假设,在征收增值税的情形下,企业的税收负担减轻,且由于研发资本投入从不可抵扣变为可进项抵扣,并且这项改革会促进生产分工与专业化水平的提高,进而会促进全要素生产率的增长。根据理论部分提出的假说2和假说3,提出以下实证回归方程
lntfpit=θ0+θ1taxit+θ2treatit+θ3taxit×
treatit+ρXit+εit
(22)
lntfpit=α0+α1RDit+α2taxit+α3treatit+
α4RDit×treatit+Xit+εit
(23)
lntfpit=β0+β1vasit+β2wvatit+β3treatit+
β4vasit×treatit+ξXit+εit
(24)
式中:εit代表随机误差项,wvatit为产业关联度,θ0、α0、β0为回归方程中对应的系数项,θ1、θ2、α1、α2、α3、β1、β2、β3、β4、γ、ξ是回归方程中相应变量的回归系数,t表示年份,lntfpit为全要素生产率,P为控制变量的系数。本文定义处理组treat在试点企业对应省份与行业实施“营改增”后取值为1,其他年份取0,样本期间实施营业税的省份与行业为对照组,取值为0;实证方程中的其他变量定义将在下一小节的变量定义中给出。根据方程,对企业实际税赋taxit和企业实行“营改增”与否虚拟变量treatit的交乘项系数θ3的估计,可考察“营改增”是否通过税赋降低这一效应提高了企业的生产效率。在式(23)中,对企业研发RDit和企业实行“营改增”与否虚拟变量treatit的交乘项系数α4的估计,可探讨“营改增”是否通过研发效应提高了企业的生产效率。而式(24)通过对企业一体化程度vasit和企业实行“营改增”与否虚拟变量treatit的交乘项系数α4的考察,可判断“营改增”是否通过企业专业化水平的上升提高了企业的生产效率。
值得注意的是,在treat的具体取值上,本文的研究目的在于评估“营改增”这一重大征税体制变革所带来的微观效应,改革的试点在地区与行业的逐步扩大,为识别政策效果带来了一定的难度,因此需要通过匹配上市企业所属地区与行业,依据相应的试点时间确定政策虚拟变量的取值。2012年,中国的“营改增”改革首先选择了上海作为首批试点地区,“营改增”改革在时间、地区、行业上具有非常明显的逐步推进向外拓展延伸的趋势。同年8月1日,试点的“1+6”行业在地域范围上由上海市分批推广至北京、天津、安徽、湖北、江苏、浙江、福建、广东等八省市,并在一年之后普及至全国所有地区,2014年1月1日起,国家将铁路运输和邮政业两个行业统一纳入试点行业,由于行业具有全国范围联动的特殊性,该行业的营业税改征增值税在全国范围内一次性地同步实施。2014年6月起,电信业也被纳入全国性税制改革试点范围,剩下的建筑业、房地产业、金融业和生活服务业4个服务行业自2016年5月开始实施改革。
(二)变量定义
1.全要素生产率(lntfpit)
鉴于数据的可得性,本文基于LP方法,参照索洛Solow使用Cobb-Douglas生产函数[13],对2000~2017年中国上市企业全要素生产率进行估算,使用的基本模型如下
lnYit=φ0+φ1lnKit+φ2lnLit+φ3lnMit+εit
(25)
式中包括3个投入变量:自由变量是中间投入变量lnMit和劳动力投入变量lnLit,状态变量是资本投入变量lnKit,Yit为利润表中的营业收入变量,对研究所使用到的变量分别做取对数处理,系数φ则分别刻画了各生产要素对于产出的贡献率,本文依据鲁晓东等的半参数方法[14],分别选择财务报表中的数据作为TFP估计模型所需要的变量;产出变量为企业的营业总收入,中间投入变量的计算使用了企业中间投入的数据,具体的计算方法为:中间投入=企业总产值-企业增加值+流转税,企业增加值=固定资产折旧+劳动者报酬+生产税净额+营业盈余;其中流转税的定义即以纳税人商品生产、流通环节的流转额或者非商品交易的营业额为征税对象的一类税收,包括增值税、消费税、关税等等。
劳动力投入变量为企业年平均就业人数,资本投入变量为固定资产净值余额,计算方法为
Kit=Kit-1+Iit-DISit
(26)
式中:Iit、Kit、DISit分别代表企业投资额、当年资本存量和固定资产折旧。
2.企业研发支出(RDit)
本文对企业研发费用的衡量采用中国会计准则委员会的标准,包括企业在产品、技术、材料、工艺、标准的研究、开发过程中所发生的各项费用。企业由于自行开发带来的研发支出,不满足资本化条件的,计入“管理费用”科目,在达到预期目的形成无形资产的,计入“无形资产”科目。本文中借鉴鞠晓生等的方法[15],使用无形资产的增量反映企业的创新活动投入,理由主要有以下3点:第一,无形资产包括企业的专利权、非专利技术、商标权与著作权等,其增加主要是企业创新投入的结果;第二,企业的创新投入并非仅包括科研支出,还包括人力资本开发、技术引进吸收等,无形资产所包括的关于企业创新活动的投入信息更多;第三,中国大部分上市公司并不披露R&D数据,财务报表中的“开发支出”一项也无法完全反映企业用于研发的费用化支出。
综上所述,本文使用无形资产的增量,并控制行业固定效应以减弱不同行业中无形资产差异所带来的影响,并将企业财务报表中的R&D支出与开发支出作为本文稳健性检验的内容。
3.企业实际税负(taxit)
目前对企业缴纳的流转税额进行测算的方法主要有两种:第一,从财务报表中获得应交增值税与营业税金及附加的总和;第二,根据教育费附加税项与城市维护建设税倒推流转税。根据数据可得性,采用前一种方法核算流转税费,而将另一种做法纳入稳健性检验中。
本文提出的基于财务报表及附注的企业流转税负衡量指标
taxit=(增值税it+营业税it)/Yit
(27)
企业税负是指在计税经济来源中企业所缴纳的各项税款所占的比重,由于正常经营的企业营业收入是其最主要的计税经济来源,因此,在设立的税负变量分母的选择中,采用了利润表中的营业收入变量Yit。
4.产业关联度(Wvatkt)
采用投入产出表进行产业关联度的测算,是学术界的常规做法[9,16],在本文中我们采用范子英等的相关做法[9],即使用2012年中国投入产出表135个部门直接消耗系数矩阵与对应行业的增值税率的乘积,以此得到各个行业的加权增值税率,用公式表示为
(28)
式中:k代表行业;Vatrate代表所涉及的中间投入行业的增值税税率,如果该行业实行营业税则税率定义为0;Directcons是指投入产出表中的直接消耗系数,两者的乘积即为所求得的产业关联度。
5.企业一体化程度(vasit)
纵观测算企业一体化的相关文献,Adelman所提出的价值增值法得到了普遍采用,所谓价值增值法,即以企业销售收入中不同产业链上的增加值所占的比重来衡量企业的一体化程度[17]。Buzzel提出了修正的价值增值法,可以代表企业所获得的正常回报,克服了传统的vas方法比较容易受到利润率波动影响的缺陷[18]。具体的衡量公式如下所示
vasit=(增加值-税后净利润+净资产×
净资产收益率)/(主营业务收入-税后净利润+净资产×净资产收益率)
(29)
式中:净资产=资产总计-负债总计+少数股权权益。本文借鉴Buzzell[18]与范子英等[9]的研究方法,衡量公式中使用的增加值等于销售额减去采购额,计算公式为
采购额=购买商品、接受劳务支付的现金支出+期初预付款-期末预付款+期末应付款-期初应付款+期初存货-期末存货
(30)
销售额=销售商品或提供劳务获得的现金流入
(31)
6.其他控制变量
本文还根据已有的研究,控制了如下影响企业全要素生产率的因素:①资本劳动比(klit),使用样本资产规模与职工人数的比例;②企业年龄(ageit),使用样本年份与企业注册年份的差值;③固定资产(fixit),使用固定资产的对数表示,以衡量资产规模;④企业所有制性质(ownerit),使用国有股控股比例变量。另外,除比例变量外,以上变量在回归中均取对数值。
(三)样本选取与描述性统计
根据“双重差分”模型的基本设定,本文选择2000~2017年“营改增”改革试点期间所涉及到的相关省份与行业上市公司的年度财务报表数据作为研究对象。在选定的“营改增”改革发生期间,对数据进行了如下筛选:剔除营业收入为负数的企业;剔除资产净额为负或为0的企业;剔除员工人数为负或为0的企业;剔除应付职工薪酬为负数的企业;剔除企业缴纳税费为负或为0的企业;剔除数据出现漏损或者数据缺失严重的企业。为了避免异常值对实证研究产生扰动,对数据进行了上下1%的缩尾处理。实证研究中使用的企业财务数据均来自国泰安CSMAR数据库,省份数据与全国数据来自各省市历年统计年鉴与历年《中国统计年鉴》。2012年,证监会对行业分类标准进行更细致的划分,因此根据2012年出台的新政策统一对样本企业所属行业划定标准。数据的基本情况如表1所示。
三、基本实证结果
本文通过实证分析验证了“营改增”改革、企业研发投入与税负、产业关联度与企业一体化程度、企业全要素生产率之间的关系。
(一)减税效应
为探究“营改增”政策是否为企业降低了税负并且提高了企业的全要素生产率,以涉及到“营改增”的企业为处理组,使用双重差分DID的方法进行评估。在基本的实证回归中,同时定义时间虚拟变量与行业虚拟变量,以此控制时间固定效应与行业固定效应。减税效应实证回归结果如表2所示。
表2中,第(1)列表明,在实施“营改增”政策后企业的全要素生产率显著提高,在此基础上将企业的税负因素纳入到解释变量中;第(2)列表明企业税负单独对企业的生产率并无显著影响;第(3)列以全要素生产率为因变量并同时加入了政策虚拟变量与企业的税负变量的交乘项,表明“营改增”政策对企业税负的降低与全要素生产率的提高有积极的促进作用,并且显著提高了税负降低对企业全要素生产率提高的作用。

表1 描述性统计
(二)企业研发效应
参考洪诗晨的研究,他们认为“营改增”政策实施对研发和技术服务业的最终影响取决于“税率变动增减效应”和“进项抵扣的减税效应”两者叠加的净效应[19]。解洪涛等采用全国税源调查数据分析了湖北省研发和技术服务业“营改增”的减税效应,发现“营改增”对于制造业研发外购具有促进作用,并且改善了具有外购行为企业的绩效[20]。另外,根据国家政策规定,“营改增”政策由于允许研发支出折扣抵税,可以显著激励企业的研发投入,在减轻企业税收负担的同时提高企业的竞争能力。基于此,本文将研发投入作为重要的解释变量纳入实证分析考量中。考虑到不同企业的经营特点,“营改增”政策对内部研发活动较多的企业有更大的影响,因此使用的企业样本是科研创新活动较为频繁的制造业企业与高新技术企业。研发效应实证回归结果如表3所示。
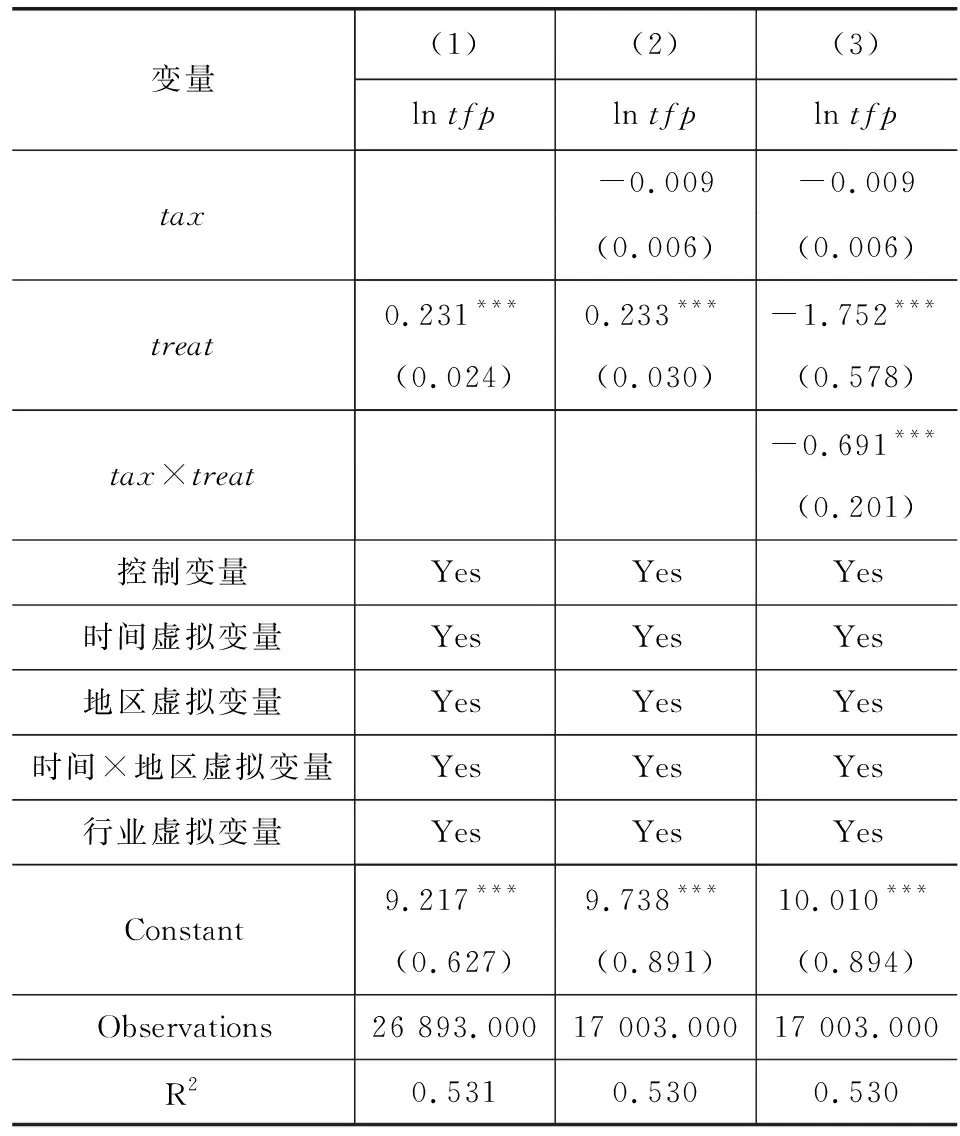
表2 减税效应实证回归结果
表3第(1)列的回归结果表明,企业的全要素生产率与研发投入之间有显著的正向关系。在第(2)列加入“营改增”政策虚拟变量与税收负担变量,可以看出在实施“营改增”后,企业的研发支出显著提高,并且随着税收负担的减轻与研发投入的增加,二者与全要素生产率之间是显著的正相关关系。第(3)列同时加入政策变量、税负变量及政策变量与研发投入的交乘项后,研发支出对全要素生产率的影响依旧保持显著正向,且交乘项的系数为正,表明“营改增”通过研发支出对全要素生产率的影响为正。这对上市的制造业企业与高新技术企业而言,税制改革增强了企业研发对生产效率的正向影响,验证了理论推导中的假说2。
(三)专业分工效应
在关于税制改革的讨论中,专业化分工水平的提高也是一个十分重要的方面。以往文献认为,增值税有利于生产分工的细化,并有效降低生产的边际成本,提高企业的生产效率[8]。因此,通过实证分析对“营改增”引致的专业分工以及产业互联水平的变化进行考察。分工效应实证回归结果如表4所示。
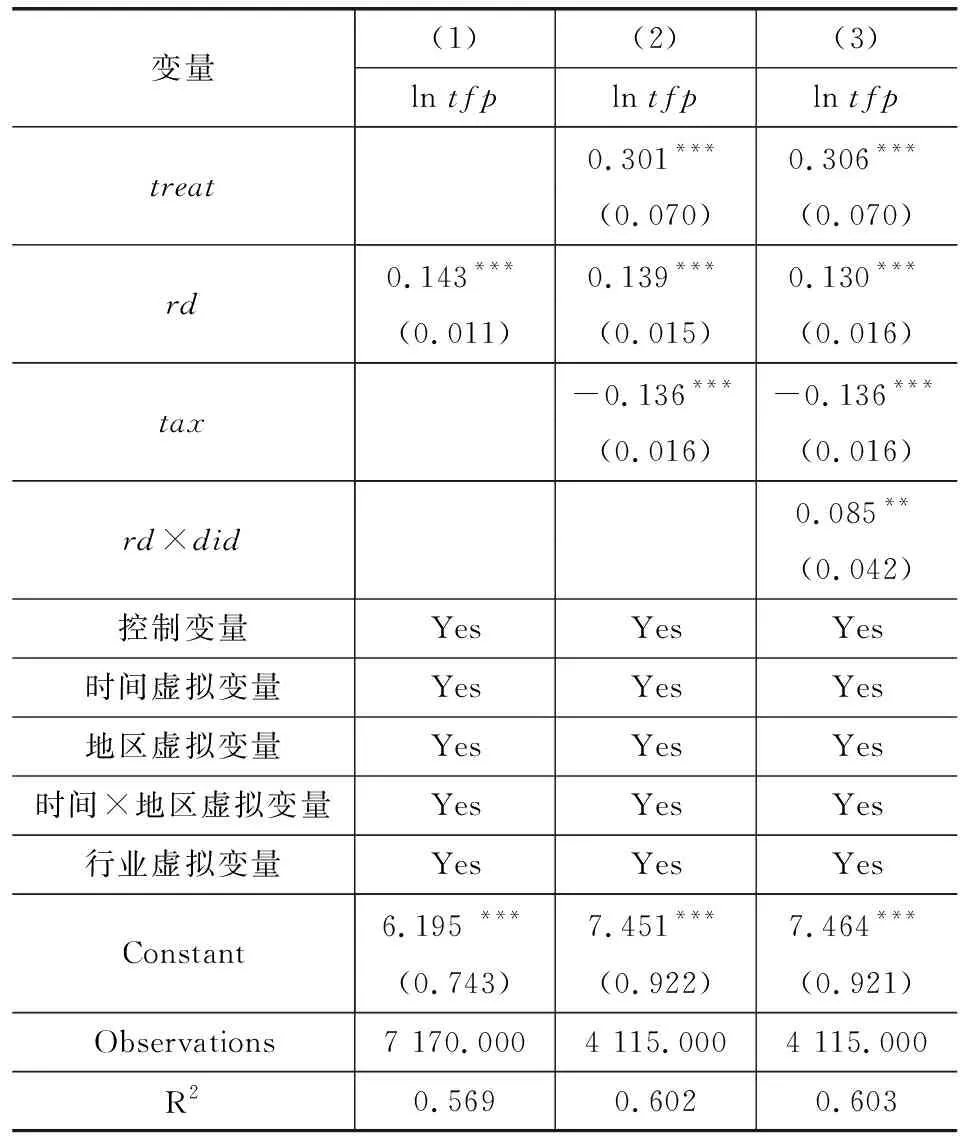
表3 研发效应实证回归结果
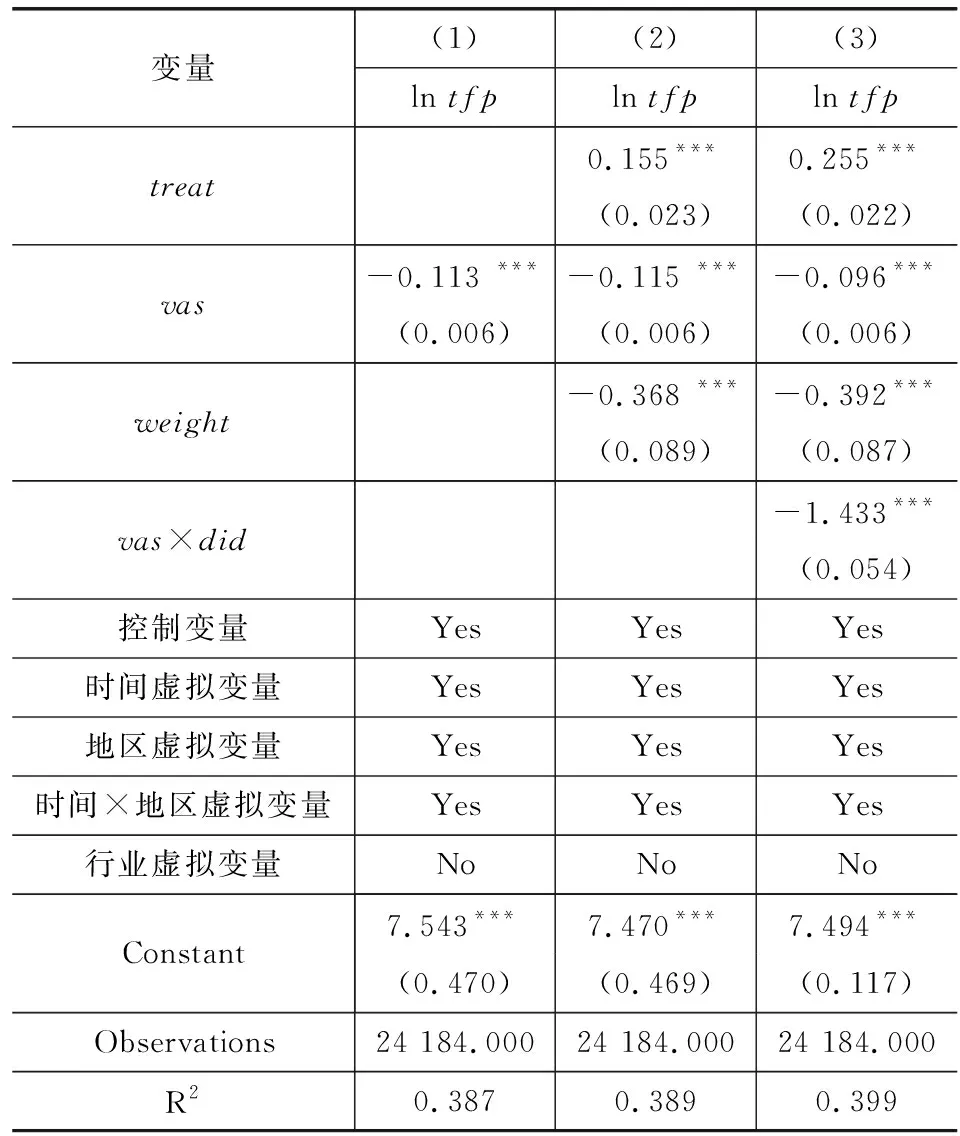
表4 分工效应实证回归结果
表4第(1)列对全部样本企业的回归表明,企业的生产一体化水平越高,即分工水平越低,企业的全要素生产率水平越低。在第(2)列的回归中表明,中国税制改革所带来的企业分工水平有所提高,但产业互联水平的变化与企业分工的变化呈现反方向变动,造成这种现象的原因有两个:一是改革时间仍然较短,成效的显现仍然需要一定的时间;
二是“分步式”的改革策略一定程度上影响了增值税抵扣链条的完整性,会降低改革的分工效应。在第(3)列的回归加入了交乘项,结果发现企业生产一体化水平对企业全要素生产率的提高依然是负向显著的影响,且由双重差分项可以得知在实施“营改增”政策后,分工水平的进一步提升会带来全要素生产率的提高,这同时验证了理论假说3。
四、稳健性检验与安慰剂检验
为了证明计量方法的准确性,对于论文的实证部分进行安慰剂检验与稳健性检验。通过改变实证方程中的某些参数、选取不同子样本,若此时核心解释变量的符号方向与显著性水平仍然保持一致,说明实证结论是稳定的。
(一)平行趋势检验
以上双重差分结果无偏的一个前提条件是实证的处理组和对照组在事件发生之前应该有相同的变动趋势,否则差分法会对事件所带来的效果产生错误估计。为了对这一前提假设进行检验,借助事件研究法来对假设进行考察,如果平行趋势的假设成立,则全要素生产率的变化只会发生在“营改增”改革之后,而在税制改革之前,改革企业与未改革企业之间的全要素生产率的变动趋势不应该存在显著差异。
为检验平行趋势假设,本文提出了如下的回归模型
(32)
式中:treati,t-j是一个虚拟变量,在年份t-j时,公司i发生了税制改革,则该变量取1,反之取0;Xit代表其他的控制变量;ρ是控制变量的系数;α为截距项,ε为随机误差项。将税制改革发生的年份设定在2012年,滞后1期、滞后2期、滞后3期分别是改革之前3年的效果,向后1期、向后2期、向后3期是改革之后3年的效果,令改革发生的2012年作为模型的基准组,系数β体现改革所产生的动态效应。由图1可得,在改革发生前β的系数在0附近徘徊,因此满足使用双重差分方法的假定。
(二)安慰剂检验
以“营改增”改革作为政策冲击验证两条分工效应与研发效应的影响,可以通过挑选出政策研究期内税制改革所没有涉及到的行业(包括建筑业、房地产业与生活服务业等)并对政策变量随机赋值所得到子样本进行检验,如果实证结果没有发现类似的因果关系,那么就说明文章的主要结论是可靠的。
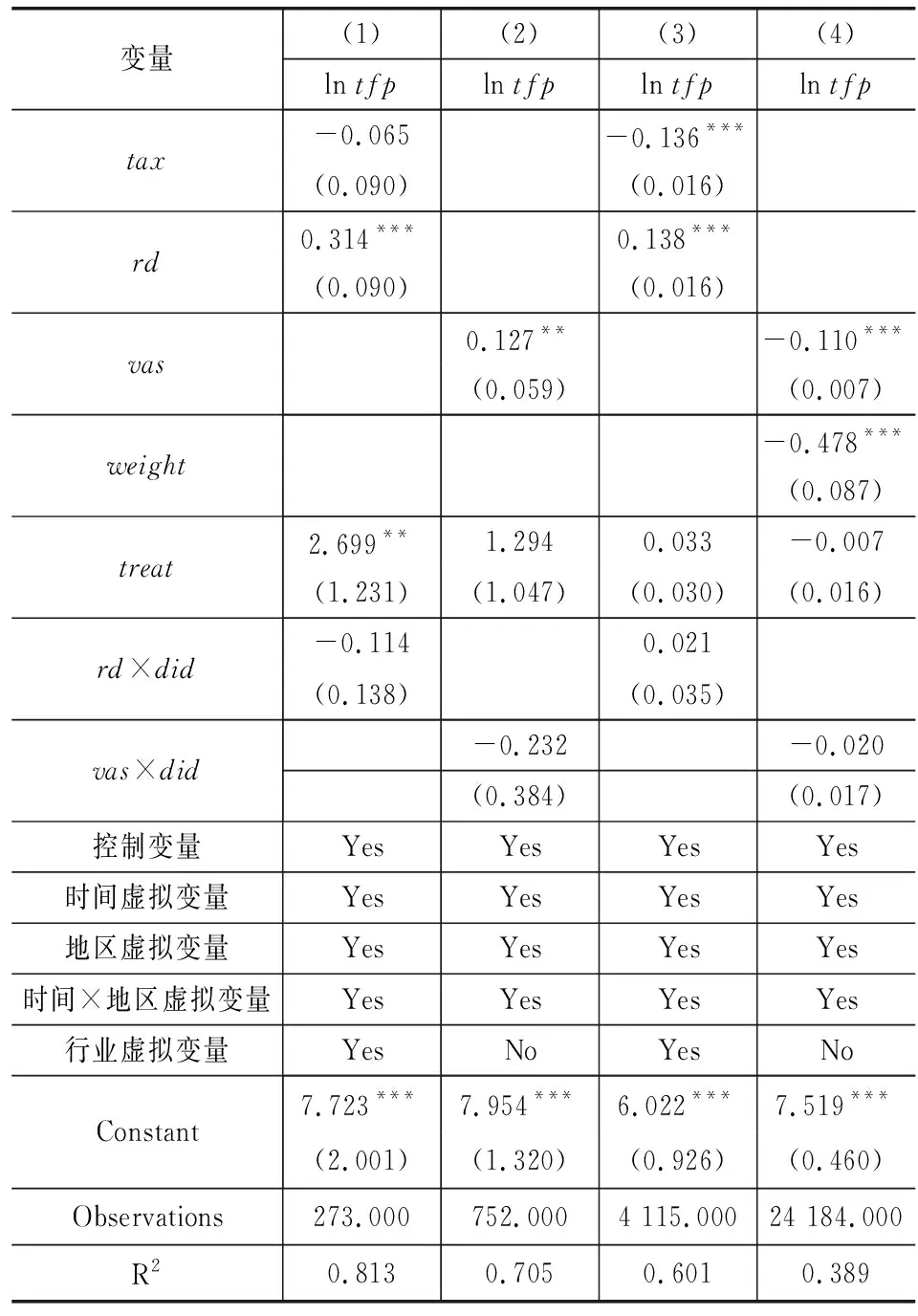
表5 安慰剂检验实证回归结果
安慰剂检验的结果如表5所示,其中第(1)和(2)列代表2016年前税制改革未涉及到的行业,对照组为所对应行业实施“营改增”后的对应样本;第(3)和(4)列代表对政策变量随机赋值所得到的子样本,可以看出在针对安慰剂检验的子样本的回归中,交乘项的系数都是不显著的。这说明“营改增”政策并没有通过本文提出的渠道对所涉及企业的全要素生产率产生显著影响,也从侧面说明了本文实证方法的可靠性。
(三)稳健性检验
1.更换生产率指标
计算全要素生产率需要妥善处理同时性偏误,必须控制相当多的不可观察因素以获得对生产函数的一致估计。Ackerberg et al.指出企业的中间投入依赖于资本、劳动与生产率,这将会导致传统的OP法与LP法在估计上有着不可识别以及内生性的问题[21]。根据其所提出ACF方法,放松了OP法与LP法的相关假设,重新估计生产函数,并测算生产率作为稳健性检验的因变量。在使用不同的生产率指标对基准方程进行回归后发现,核心解释变量的系数仍然保持稳健。表6第(1)列中“营改增”所带来的减税作用对全要素生产率仍然有积极的正向影响,第(2)列与第(3)列中研发支出与产业关联水平对全要素生产率的影响依然显著为正,这说明“营改增”政策实施后,企业全要素生产率有了显著提高。

表6 ACF法计算TFP实证回归结果
2.改变计量方法
稳健性检验也可以从改变计量方法着手,考虑到本文实证中所使用的上市企业数据库面板数据,在表7第(1)列采用面板固定效应、第(2)列采用面板随机效应回归来检验实证方法是否稳健。在稳健性检验中发现,通过研发渠道对全要素生产率的影响实证中,交乘项系数依然保持正向稳健,而通过减税渠道对全要素的回归中,企业的税负水平与全要素生产率依旧保持显著的反向关系,由此得出结论:实证结果是稳健的。
3.选取不同的解释变量指标
依照前文变量定义中的划分,分别使用不同的解释变量来对基准实证模型进行检验稳健性。在表8第(1)(2)和(3)列中,分别通过城建税与教育费附加倒推、使用利润表中的营业税金及附加以及现金流量表中企业缴纳税款的进项与销项之差这3种不同的方法来替换企业税负指标,在第(4)和(5)列中,分别通过财务报表附注中的研发支出与资产负债表中的开发支出代替企业自主创新的费用支出,并分别对子样本进行实证回归并观察系数变化,以此确认“营改增”与企业税负对全要素生产率的影响是否稳健。
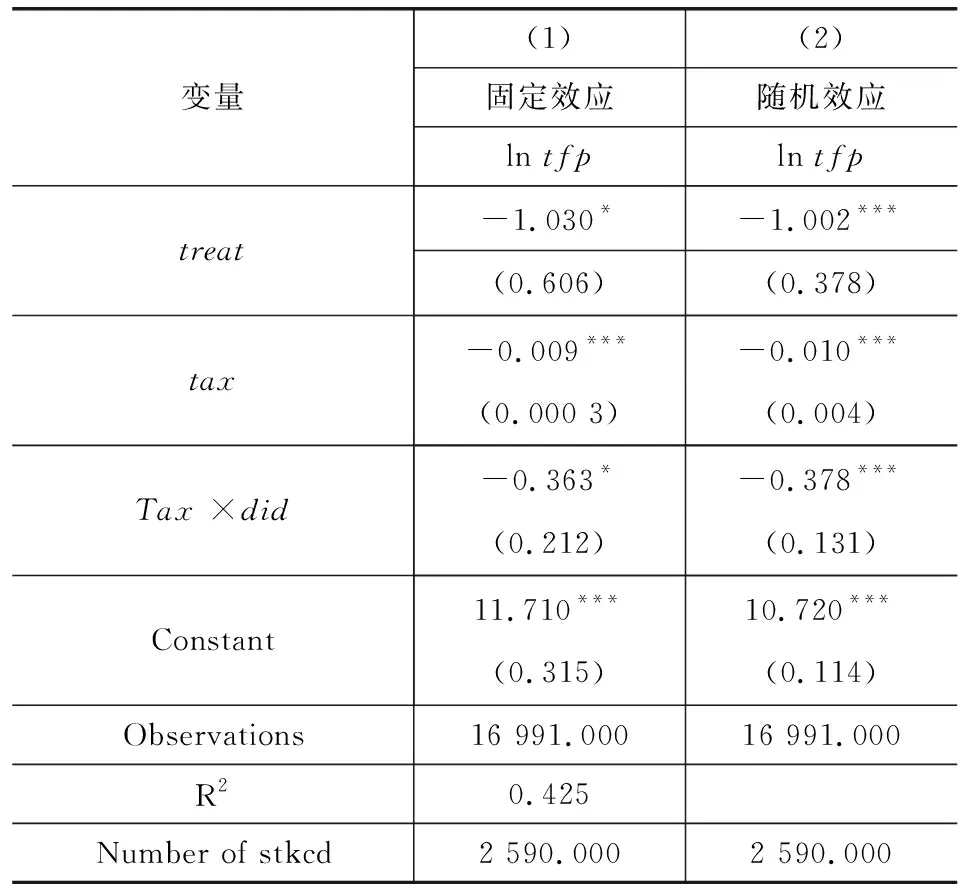
表7 面板数据实证回归结果
根据分样本回归后的结果发现,所有子样本的税负水平与全要素生产率之间的关系是负相关的,且在第(1)(2)和(3)列的回归当中,税负水平的降低促进了全要素生产率的提高,这与基准方程中的结果是一致的。在第(4)和(5)列的回归中,对每一列的实证回归进行进一步分析,可以发现稳健性检验的交乘项系数与前文保持一致,进一步验证了实证结果是稳健的。
4.示范外溢效应检验
税制改革具有强烈示范与外溢效果,往往“牵一发而动全身”,在税负减免的条件下,企业往往会选择外包企业的非主营业务以获得效用提升,而对于获得外包的整个地区企业效用提升都有积极作用。因此,在稳健性检验中,企业如果在某年份属于涉及到“营改增”改革的省份,则令其值为1,否则将其值设定为0。将新设定的treat政策变量用作解释变量并再次分别与企业税负、研发投入与分工水平变量作交乘,以此进行检验。可以看出,在替换了did变量后,表9显示的实证结果依然保持稳健,这不仅表明了实证结果的稳健性,同时也说明企业研发与行业分工具有外溢效应,带动了整个地区生产效率的提高。

表8 替换解释变量指标实证回归结果

表9 示范外溢效应检验实证回归结果
五、进一步的分析
接下来,根据不同的标准对数据进行分组,并确定样本的四分位数。在本文的进一步分析中,依据资本密集度、企业规模与产业关联度对数据进行排序,分别挑选出资本密集度、企业规模与产业关联度较高的前50%,资本密集度、企业规模与产业关联度较低的后50%,作为本节实证回归的子样本,通过比较组间差异论证本文理论模型中的假设。
(一)企业研发的熊彼特效应
袁从帅等选取上市公司通过实证发现“营改增”改革显著提高了人均资本量,并一定程度上有益于企业的研发投入[22];另外,依据熊彼特创新效应理论[23-25],企业的创新投入与企业的自身特质、行业环境密不可分。“营改增”政策会改变企业的研发环境,可以激发更多企业的创新活力。据表10所示,企业的研发投入可分为资本投入与人力投入,其中资本投入在征收增值税的情形下可抵扣,因此依据资本密集程度对企业样本进行划分所得到的表10中第(1)和(2)列的回归结果,可以看到高资本密集度的企业,在实施“营改增”后,研发投入对全要素生产率的效应显著增强,而资本密集度较低的企业,“营改增”发生所带来的研发投入对全要素生产率的增加有限,且交乘项系数不显著,这表明“营改增”通过研发渠道与全要素生产率产生关系是借助企业的研发资本投入抵扣这一方式的影响,且资本投入越高,影响越大,由此验证了本文的假设2。表10中第(3)和(4)列分别报告了企业规模异质性下企业研发对全要素生产率的影响差异,该回归结果表明,研发投入对全要素生产率的影响存在规模效应,企业规模越大,研发投入对全要素生产率的提升幅度越大。由此可以看出,大企业的研发投入对全要素生产率的提升水平更高。
(二)专业分工的关联效应
据本文的理论推导与范子英等的观点,企业的专业化分工水平对全要素生产率的影响会因为产业关联度水平的高低而产生不同的影响[9],因此需要对分工效应展开进一步的探究。如表11所示,在(1)和(2)列的回归中,企业一体化程度与全要素生产率的关系显著为负,交乘项的系数也显著为负,说明税制改革后企业分工水平的提高会带来全要素生产率的提高。比较两者的系数可以发现,规模大的企业实施“营改增”后,企业一体化水平对全要素生产率的影响更强,显著性水平更高,规模效应较为明显。第(3)列的回归显示,企业的分工水平与全要素生产率正相关,但在实施“营改增”政策后,企业的分工水平对全要素生产率存在显著的负向影响,即税制改革后,对于产业关联度较低的企业而言,分工水平的提高反而降低了企业的全要素生产率,这表明在增值税抵扣链条不完整的状态下,企业实际的成本可能加重,不利于全要素生产率的提高。第(4)列的回归则显示,在实施“营改增”政策后,高产业关联度企业的分工水平对全要素生产率有显著的正向影响,由此验证了本文的假说1,即对于处于产业链较完善的行业中的企业而言,专业化水平的提高可以降低生产的边际成本,进而促进全要素生产率的提高。

表10 分样本研发效应实证回归结果

表11 分样本分工效应实证回归结果
六、结语
在中国的税制改革过程中,伴随着试点范围的逐渐扩大,“营改增”政策对中国的资源配置效率产生的提升作用逐步加强,通过构建理论模型并实证检验“营改增”政策对全要素生产率的影响,且通过双重差分模型的逐步检验发现存在减税效应、研发效应和分工效应,并得出了以下结论。
第一,在实施“营改增”政策后,企业的实际税负有了明显降低,税收成本的降低有力地促进了全要素生产率的提高;且根据我们回归的结果,企业的资本密集度、资产规模、产业关联水平越高,全要素生产率的提升幅度越大。
第二,由于实施增值税所带来的研发支出可抵扣,在实施“营改增”政策后企业的研发投入普遍增加,企业的全要素生产率与企业的研发支出具有显著的正向关系。由于可抵扣的部分是研发支出的实体资本部分,因此依据资本密集度划分企业样本,可以发现“营改增”政策显著增强了高资本密集度企业研发支出对全要素生产率的正向影响,而对低资本密集度企业的影响则不显著。从规模效应来看,尽管就系数大小而言大规模的企业研发投入对全要素生产率的影响更大,但“营改增”显著增强了中小企业研发投入对全要素生产率的正向影响,对中小企业的科技研发具有积极的促进作用。
第三,本文还验证了“营改增”政策实施后企业专业化分工水平的提高。“营改增”政策使得企业更加注重专业化经营,降低生产的边际成本,提高分工水平。但产业关联度对企业分工具有负向的消极作用,原因一方面可能是“营改增”对产业结构的整体影响尚未完全显现,另一方面可能是分行业逐步推进的改革破坏了行业关联链条的完整性,使得产业关联度对企业分工水平的影响不符合预期;而专业化分工水平和产业关联水平的提高都促进了生产效率的提高,这与本文的理论假设是相契合的。在依据产业关联度划分企业子样本的回归中发现,税制改革增强了高产业关联度行业中的企业专业化分工水平对全要素生产率的影响,对低产业关联度行业的专业化分工提高全要素生产率的影响有着负面的消极作用。
本文的实证结果从各个方面验证了减税效应、研发效应和分工效应显著提高了中国企业的全要素生产率,为评估“营改增”的成果提供了事实依据。本文认为“营改增”是一个逐步推进的过程,其效果在目前来看尚未全部显现,但“营改增”对于企业减负、企业创新与分工协作有着明确的积极意义。根据以上结论,本文提出如下政策建议:第一,继续坚定地深化落实“营改增”政策,减轻企业税负,为促进资源跨地区的合理配置打下坚实的政策基础;第二,鼓励处于价值链底端的企业转向价值链高端的生产活动,尤其是鼓励制造业企业从产品加工环节转向服务化,提高企业的分工效率;第三,税制改革对于行业上下游重复征税的削弱作用成效显著,应该继续深化改革,打破财政分权壁垒,促进要素的自由流动。

