提供补救服务情境下专家薪酬、服务优化对服务策略的影响研究

李武强 刘德智 许晓晴

(长安大学经济与管理学院)

1 研究背景

在一些面对面的专家服务中，受专家能力、服务过程设计的合理性以及技术发展水平等因素影响，服务失败难以避免[1～3]。为了减少顾客损失，维持良好声誉，服务方往往会把免费重新提供服务作为重要的补救方案[4,5]。例如，在医疗美容行业中，部分企业会承诺为服务失败的顾客免费提供二次服务，并将其作为重要宣传手段；在一般医疗服务中，对于由医生过错导致的服务失败问题，一些医院也会免费再次治疗；相似的情况在心理咨询相关服务中也经常存在。

排队等待是面对面专家服务的常见问题，特别是在拥有知名专家、优质服务资源的服务场所中[6]。而对于将重新服务作为补救方案的商家而言，因服务失败而返回服务点的顾客将会导致更长的排队队列，尤其是在服务失败概率较高的情况下，这一问题更为严重。考虑到等待成本对于顾客服务选择的重要影响，以及排队论在分析服务系统方面的优势，许多研究者基于具有反馈回路的排队网络，对上述问题从系统优化的视角进行了研究：如DE VÉRICOURT等[7]对服务失败时顾客会重新申请服务的问题，基于服务小组拥有不同的服务速度μ与成功率p的假设，提出了能够实现逗留时间最短的pμ规则；CHAN等[8]针对服务速度依赖于需求规模与系统负载的现象，构建了服务失败后顾客需要在其他服务点先接受服务，才能再次等待服务的排队网络，证明了服务加速行为的有效性。另外，还有学者从服务提供者收益优化的视角进行研究，如GUO等[9]在考虑到达成本的基础上，基于理性服务提供者的假设，探讨了公共服务系统中，一次性付费与按服务次数付费两种报销机制对服务速度、社会福利的影响；WANG等[10]考虑患者复诊的情况下，针对两级医疗模型，探讨了转诊费用对患者预期效用、等待时间的影响。然而，上述研究中服务失败属于概率事件或者与服务时间相关，较少考虑到专家能力的影响。

如何选择专家也是必须要考虑的重要问题。高能力的专家往往能够带来良好的服务体验[11,12]，同时其薪资待遇要求也较高；而雇佣一般水平的专家，则有可能导致客源减少、收益下降的问题。针对这一现象，部分学者基于能力与薪酬正相关的假设，对专家的选择与管理进行了研究，如周华等[13,14]针对专家服务中服务时间与服务质量正相关的特征，以收益最大化为目标探讨了专家选择以及服务定价等问题；KIM等[15]则在对病人护理质量与医生薪酬统计分析的基础上，建立了医生的分级方法。然而，由于研究重点的不同，上述文献并未考虑专家能力与服务失败的相关性问题。

此外，服务行为是否规范、过程是否合理也是决定服务效果的重要因素[16]。在此方面，唐建生等[17]基于实验研究的方式，针对由服务过程不合理导致的服务失败现象，探索了顾客对服务人员、效果的评价问题，并提出了优化服务组织方式的建议；岳英等[18]从服务人员的着装、处理及时性角度探讨了顾客对服务失败的感知模型，并基于此提出了改善服务过程的相关建议；杜建刚等[19,20]基于实验研究，对服务人员的负面情绪、服务态度等因素如何影响消费者效用、满意度进行了探索。然而，上述研究均定位在不更换服务人员的情境下，如何从服务组织或者行为引导等方面减少服务失败的问题。

综上可知，在面对面专家服务领域，已有研究较少关注在以重新服务作为补救方案的情境中，如何选择合适能力专家的问题。同样，下述面对面专家服务中的常见现象与问题，目前还未得到充分的研究：①为服务失败的顾客免费提供“一次”(方案1)、“无限次”(方案2)重新服务的机会是常见的两种方案，二者在实施中有何差异？对专家的选择、定价有何影响？②虽然高能力专家的服务失败概率较低，但是在专家的选择方面依然存在两种较为矛盾的现象：一方面，部分企业考虑到薪酬成本问题，在选择高水平专家时慎之又慎；另一方面，部分企业又不计成本地引入顶级专家。上述两种现象是否合理？薪酬水平又如何影响企业选择？③一般情况下，通过对服务重点环节、过程的优化改进，可以使专家的能力得到更充分的发挥，达到更好的服务效果[21]，这种现象又如何影响专家的选择？

针对上述问题与现象，本研究从专家的能力、服务优化水平等视角展开分析，探索其内在机理，以期在服务方案、人员选择、服务定价等方面为企业决策提供借鉴，改善服务系统。

2 一次补救服务方案

2.1 模型假设

在面对面专家服务领域中，假定某服务商通过雇佣员工提供服务，并承诺服务失败时提供一次补救服务，且服务补救方式为免费重新服务。顾客是理性的，首次到达服务点后，根据预期服务效用、等待成本以及服务价格，综合判断是否选择服务。考虑到部分专家服务中服务效果体现的延迟性[22](如医疗美容)，在服务结束后顾客都会暂时离开服务点。当顾客发现服务失败时，会选择补救服务并重新排队(见图1)。

图1 提供一次补救服务(重新服务)的服务流程

在重新服务这一补救措施下，较高的服务失败概率将会导致大量的顾客返回服务点，造成等待成本的上升以及实际服务效率的下降。鉴于等待成本是顾客选择服务的重要影响因素，以及排队论在描述服务过程、分析排队现象方面的优势[23,24]，本研究针对上述问题，采用具有伯努利反馈的M/M/1模型进行研究，其中潜在需求的到达服从参数为Λ的泊松分布，服务速度服从参数为μ的负指数分布，服务时间t=μ-1，服务规则为先到先服务(FCFS)。

2.1.1服务成功率与员工能力

由现实情境可知，服务成功率不仅与专家的能力正相关，还与其发挥程度相关。不合理的服务流程、简陋的服务设备都会导致专家的能力无法得到应有发挥，造成较差的服务效果。同样，通过服务环境的改善、操作规范的改进，以及设备升级等服务优化方式，也可以使专家的能力得到更充分的发挥[25]，达到提高服务成功率的效果。本研究不考虑由培训、革命性技术设备引入等情况所造成的专家能力得到提升的现象，因此，服务优化所导致的服务成功率提升不会超过专家的最高水平。基于上述原则，借鉴文献[22，26]中服务质量为关于服务时间递增凹函数的描述，构建服务成功率(即每次服务时的成功率)β函数如下：

(1)

由于服务失败更多是由外在环境、个人能力等因素导致，不完全受专家主观控制；同时，考虑到服务方式与效果之间作用机理的复杂性，在重新服务中往往也难以明确失败的关键原因，一些研究假定服务成功率与服务次数是相互独立的[9]。为了简化分析，本研究沿用了这一假设。

2.1.2均衡排队系统相关指标

结合图1对均衡状态下的服务系统参数进行分析：假定选择服务的顾客为有效需求，其到达服从参数为λ1的泊松分布；首次服务完成后，顾客暂时离开服务点，当其感觉到服务失败时则返回，定义此类顾客为二次服务需求，到达速率为λ3，可知λ3=(1-β)λ1；总需求为有效需求与二次服务需求之和，即λ2=λ1+λ3=(2-β)λ1。

2.1.3专家薪酬

结合能力越高薪资水平就越高的现实情境，本研究在借鉴文献[14]的基础上构建了基于服务时间的薪酬支付函数：服务成功后，为能力水平为l、每次服务时长为μ-1的专家支付薪酬s=γlμ-1。其中，γ表示能够达到100%服务成功率的单位时间薪酬(简称标准时薪)，γμ-1可以看作为服务一位顾客的标准薪酬；服务失败时，专家不会获得薪酬。由此可得，专家薪酬s=Aβ，其中A=γ(1-αμ)μ-1。

当有效需求为λ1时，获得成功服务的期望需求为β(λ1+λ3)，此时专家共可获薪酬(2-β)βλ1s，这也意味着专家服务一位顾客的期望薪酬se=(2-β)βs。假定服务商是理性的，仅当其收益非负时才会提供服务，即服务价格p≥se。

2.1.4顾客选择服务的边界条件

服务成功时顾客所获效用即为服务价值ub，失败则为零。考虑到排队等待是影响顾客服务选择的重要负面因素[28]，构建顾客期望净效用Un=ue-Ce(l,λ)-p，其中ue=(2-β)βub，表示顾客的期望效用。

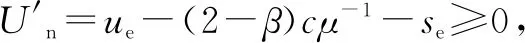
2.2 服务商决策分析

当所选专家能力水平为l且服务价格p确定以后，顾客根据判定条件Un≥0决策是否选择服务，可知存在以下3种情况：①当ue-(2-β)c[μ-(2-β)Λ]-1-p≥0时，所有顾客选择服务；②当ue-(2-β)cμ-1-p<0时，没有顾客选择服务，此情境缺乏现实意义，不予分析；③其余情况下，部分顾客选择服务。

对于价值为ub的专家服务，服务商会选择适当的价格，使得顾客净效用Un=0；否则，若Un>0，服务商总是可以在维持有效需求不变的情况下提高价格，从而获取更大收益。基于上述情境，以Un=0为临界条件，可得有效需求：

λ1(p,l)=

(2)

式(2)中，由上至下分别为所有顾客选择服务和部分顾客选择服务情境，易知有效需求为价格的连续非增函数。从服务商角度，将服务所有顾客的策略定义为Sf，将服务部分顾客的策略定义为Sp。

综上可知，面对有效需求λ1(p,l)，服务商共收取服务费用pλ1(p,l)，支付专家薪酬seλ1(p,l)，服务商的目标函数为

(3)

由式(3)可知，本研究最优策略的求解思路为：首先，找到一定能力水平专家情境下的最优服务定价p(l)；其次，对于l∈Ω的备选专家群体，根据已经得到的p(l)，探索选择什么能力水平的专家才能使服务商收益达到最大。

2.2.1服务价格

当专家能力一定时，服务商总是可以通过调整价格获取最大收益，由式(3)求解可得基于专家能力水平的最优价格决策。

定理1当服务商选择能力水平为l的专家时，其最优的价格决策为

(4)

(5)

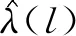
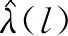
基于定理1价格策略可知，若选择Sp，则当服务商雇佣更高能力的专家时，一方面，顾客的期望效用增加；另一方面，二次服务需求比例降低，导致顾客期望效用与期望等待成本之间的差距进一步扩大，为更多顾客选择服务提供了空间，因此有效需求随之递增。但由于专家能力较高(l>μub(2γ)-1)时，薪酬支出也较高，且过多的顾客会导致等待时间延长，使得顾客总体支出处于较高水平，因此，临界需求并不总是随专家能力的提高而增加。

2.2.2对专家能力的要求

将定理1所述的价格决策p*(l)代入式(3)，求解可得关于专家能力水平的最优决策。由分析过程可知，服务价值与专家薪酬的比值在很大程度上影响了最优策略的表述，因此下文基于服务价值与专家薪酬对服务情境进行分类，并分别描述了最优策略。

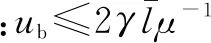
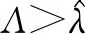
在需求足够大的情况下，服务优化水平α的提高将会导致服务成功率β*的上升。这是因为当潜在需求足够大时，对专家能力的要求是一定的，通过服务优化可以使专家的能力得到更充分的发挥，提高服务成功率与顾客期望效用，降低总需求中二次服务所占比例(λ3/λ2)，为更多顾客选择服务提供空间。从最优策略的运作来看，服务优化程度的提高不仅扩大了有效需求，还提升了服务价格，但服务一位顾客的薪酬支出却维持不变。

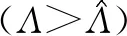
由专家能力l*的表述可知，服务商对专家能力的要求关于标准时薪γ递减。现实中，当薪酬水平提高时，若维持选择专家的标准不变，则服务商成本支出上升；若选择较低能力的专家，则必然导致服务成功率的下降，面临两难问题。从定理3a来看，选择较低能力专家的策略更优，其所节省的薪酬支出要大于服务成功率下降以及顾客流失所造成的损失。最后，需要注意的是，标准时薪的减少，可能会使服务类型从普通服务转变为超值服务，最优策略也随之改变。

定义G(β)=3Aβ2-2(ub+2A)β+2ub+μc[μ-(2-β)Λ]-2。

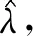
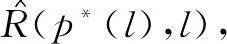
与定理3a不同，当潜在需求较小时，l*关于α递减，而β*则相反。这是因为在不更换专家的情况下，服务优化会导致服务成功率的提升以及二次服务需求的下降，但此时潜在需求是一定的，不会有新的顾客选择服务，实质上造成了服务能力的过剩，因此，最优策略选择较低能力的专家，不仅能够节约薪酬支出，同时还使系统的服务能力与需求重新达成平衡。从服务效果来看，虽然选择了较低能力的专家，但由于服务优化程度得到提升，服务成功率要高于原来水平。

与定理3a所述策略Sp相似，服务商关于专家能力的决策l*以及服务成功率β*均关于标准时薪γ递减，其原因也类似。总体而言，对于普通服务，在任何需求水平下，当薪酬水平提高时，服务商的最优策略都是选择较低能力的专家。

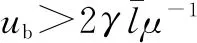
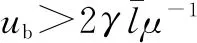
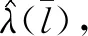
3 无限次补救服务方案

无限次免费补救服务方案下，只要服务失败顾客就可以回到服务点等待服务，直到成功为止，其他假设与方案1相同(见图2)。由此，补救服务需求λn3包含了所有非首次到达服务点的顾客，从均衡队列状态来看λn3=(1-β)λn2。又因为服务总需求λn2=λn1+λn3，因此可知λn2=λn1β-1。

图2 提供无限次补救服务(重新服务)的服务流程

与方案1类似，可知均衡状态下的期望等待成本Cne(l,λ)=c(βμ-λn1)-1。假设顾客可以选择m次免费补救服务，m∈N且m→+，可得顾客期望净效用

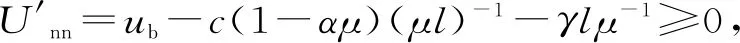
λn1(p,l)=

(6)

顾客获得成功服务的期望概率为100%，因此为其提供服务的专家可获得的期望薪酬为γlμ-1。基于服务商收益最大化构建目标函数为

(7)

对上式求解可得以下结论。

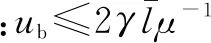
由式(7)的求解分析可知，方案2最优策略的表述同样受到服务价值与专家薪酬比值的影响，且其关于服务情境的划分与方案1是一致的。

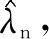
方案2的最优策略与方案1具有一定的相似性：①根据潜在需求的不同，两种方案下的最优策略均分为服务全部顾客与部分顾客两种情形；②在服务部分顾客的情形中，两种方案对专家能力的要求、服务成功率以及服务商收益均是相同的；③两种方案中最优策略所选择的专家的能力、服务成功率等因素，与潜在需求、标准时薪以及服务优化水平的相关关系具有相同的性质。

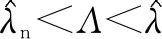
推理1普通服务中，无限次免费补救服务方案的最优服务价格是固定的。

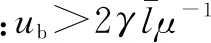
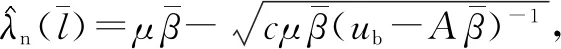
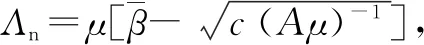
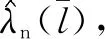
最后，对超值服务情境下的方案1与方案2进行对比分析，其结果与普通服务情境的对比相似：①两种方案在服务部分顾客阶段均选择了能力最高的专家，服务商收益是相同的，但方案2服务价格较高，有效需求较低；②在服务全部顾客且选择最高能力专家的阶段，均通过降低服务价格来吸引顾客。

4 算例分析

4.1 方案1与方案2最优策略验证及对比

分别基于普通服务、超值服务情境对方案1与方案2最优策略的有效性进行验证，并对比分析了潜在需求增加时，两种方案在收益、服务价格、专家能力要求以及顾客期望等待成本之间的差异性。

(1)普通服务

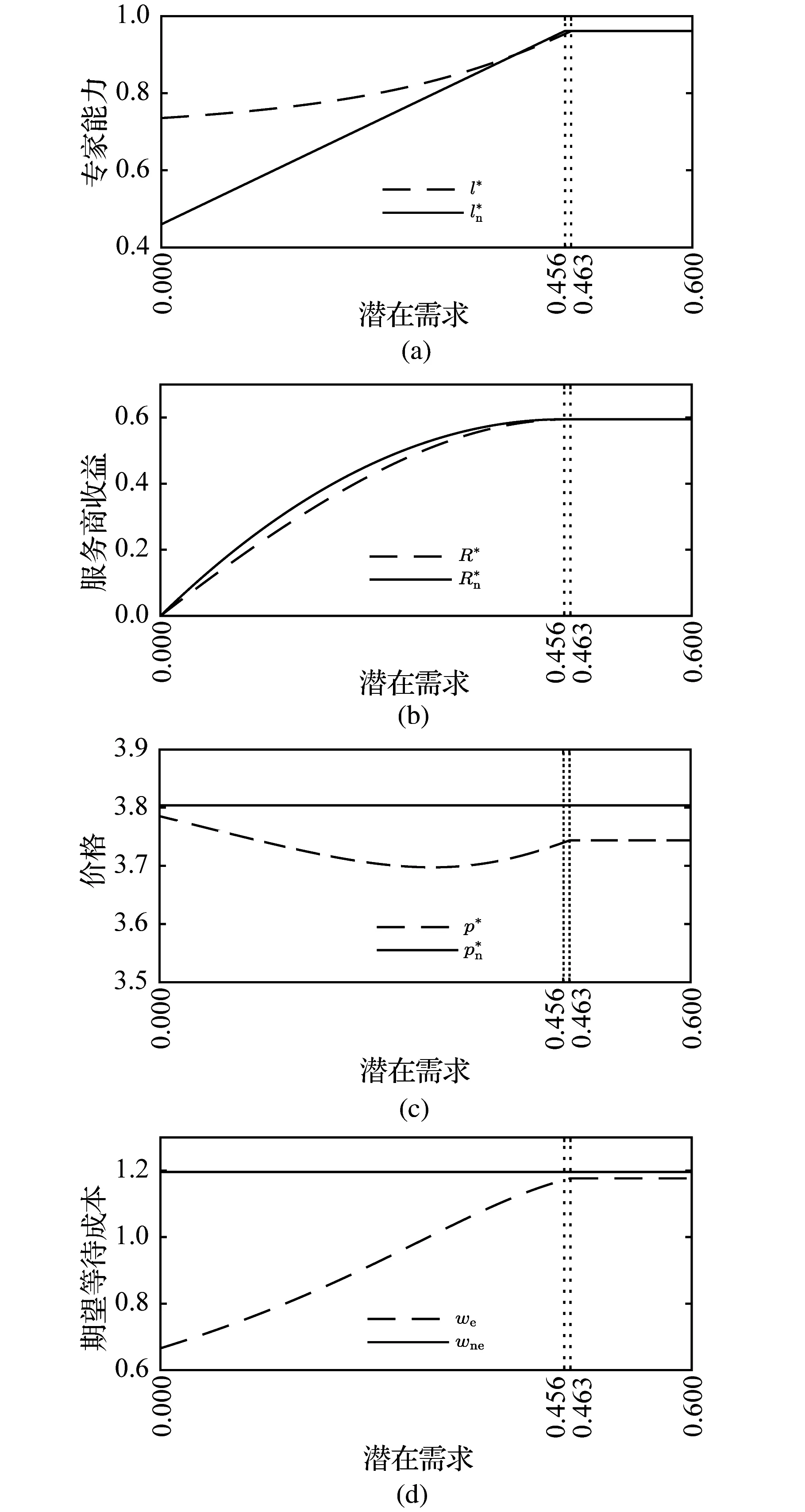
图3 普通服务背景下两种方案的验证与对比

(2)超值服务

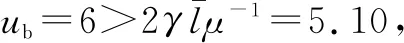
由定理4可知，方案1的最优策略可以分为Λ∈[0,0.459]、(0.459,0.538]、(0.538,+)3个阶段，其中前两个阶段选择Sf，第三个阶段选择Sp，且在第二个阶段受备选专家能力上限影响，只能选择能力最高的专家。超值服务背景下两种方案的验证与对比见图4。由图4(a)和(b)可知，方案2的最优策略可分为Λ∈[0,0.473]、(0.473,0.532]、(0.532,+)3个阶段，与方案1类似；与普通服务相同，方案2更早地达到了最大收益。两方案在服务定价与期望等待成本方面的表现与普通服务情境相似，但在第二阶段为了满足服务所有顾客的要求，都降低了服务价格。另外，由图4(c)可知，在服务所有顾客阶段方案1的价格并非总是低于方案2，但在服务部分顾客阶段则严格低于方案2。

图4 超值服务背景下两种方案的验证与对比

4.2 薪酬水平对服务系统的影响

潜在需求一定时标准时薪对服务系统的影响见图5。由图5(a)可知，随着γ的增大，服务类型由超值服务转变为普通服务，且无论是在超值服务阶段还是在普通服务阶段，临界需求均关于γ递减。当临界需求大于潜在需求(γ∈[0,2.94])时，选择服务所有顾客，相反(γ∈(2.94,11.36])则选择服务部分顾客。由图5(b)可知，从对专家能力的要求来看，当γ∈[0，2.08]时，由于薪酬水平较低，因此应选择能力最高的专家；当γ∈(2.08，2.94]时，需要结合策略Sf，根据γ的提高程度适当降低对专家能力的要求；当γ∈(2.94，11.36]时，选择能力水平l*=μub(2γ)-1=2.5γ-1的专家。由图5(c)可知，价格是关于γ的非增函数。由于方案1与方案2中γ对服务系统的影响较为相似，因此仅展示方案1情境。

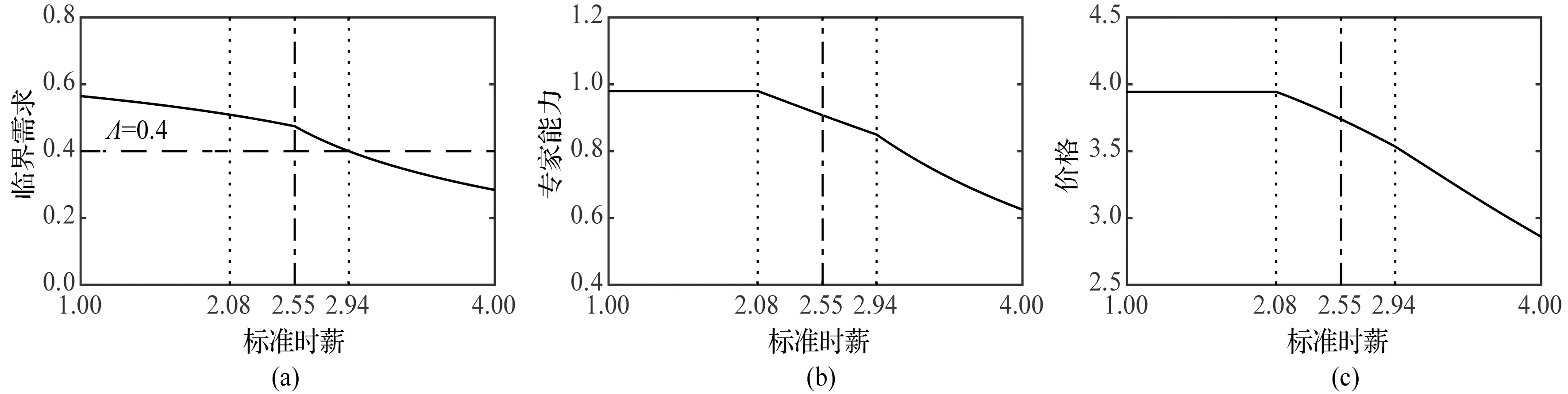
图5 潜在需求一定时标准时薪对服务系统的影响

4.3 服务优化水平对服务系统的影响

普通服务中服务优化水平对服务系统的影响见图6。由图6(a)可知，临界需求关于α递增，这实质上反映了服务优化对于系统服务能力的提升；当α∈(-3.81,-0.25)时，潜在需求大于临界需求，服务商选择Sp；当α∈[-0.25,0)时则相反，服务商选择Sf。由图6(b)可知，α在服务全部顾客与部分顾客两种策略下的作用效果是不一样的：在服务部分顾客阶段，服务优化不会影响对专家能力的要求，但会提高服务成功率与有效需求；而在服务全部顾客阶段，潜在需求有限，服务优化导致系统服务能力过剩，最优策略中服务商通过选择较低能力的专家，达到了降低服务成本、提高服务成功率的双重目的。由图6(c)可知，服务定价关于α递增。超值服务背景下服务优化对决策的影响与图6类似，不再赘述。

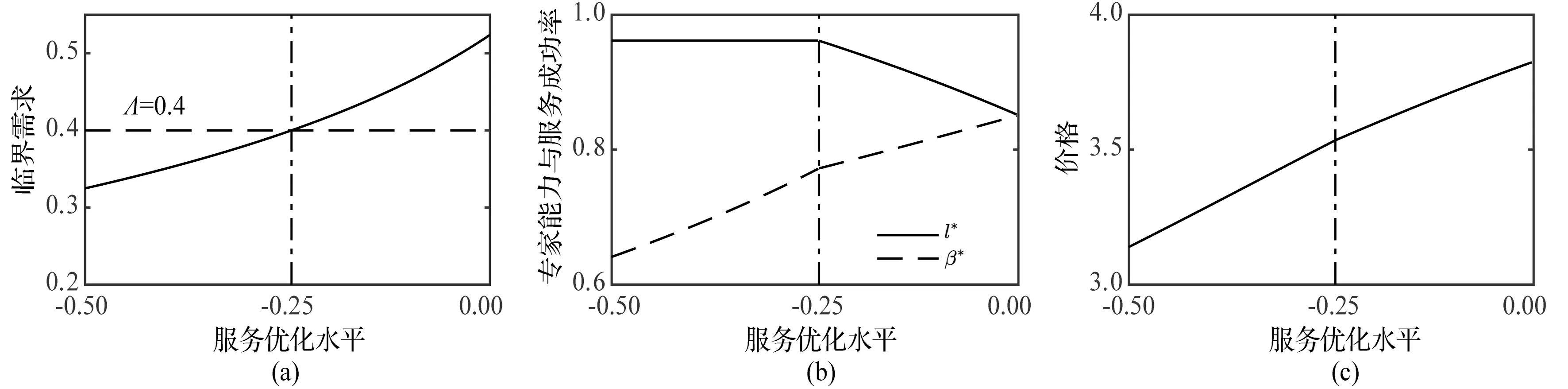
图6 普通服务中服务优化水平对服务系统的影响

5 结论

基于具有反馈回路的M/M/1模型，对将免费重新服务作为补救方式的面对面专家服务进行研究，探讨了提供一次(方案1)、无限次(方案2)重新服务机会两种方案的差异性，并从薪酬以及服务优化的视角对最优策略进行了分析，主要研究结论如下。

(1)根据服务价值与薪酬水平可将服务分为普通服务、超值服务，两类服务具有以下特点：①当潜在需求较小时，服务全部顾客，且随潜在需求增加选择更高能力的专家，但超值服务中对专家能力的要求还会受到能力水平上限的影响；②当潜在需求足够大时，服务部分顾客，其中普通服务对专家能力的要求仅与服务价值、标准薪酬相关，而超值服务则必然选择能力最高的专家，这也在一定程度上反映了高附加值服务中“一流”专家的重要性。

(2)方案2与方案1相比，具有以下差异：①当潜在需求足够大且两方案都选择服务部分顾客时，二者对专家能力的要求、服务商收益是相同的，但方案2的有效需求更低、价格更高，且在此阶段所选择的专家能力越低，二者差距越大；②方案2的服务定价更加稳定。从服务运营的角度而言，提供无限次重新服务机会的方案，对于服务商在顾客群体中建立稳定、可靠的品牌形象是有利的。

(3)薪酬是决定专家选择的重要因素，对于顾客数量有限的面对面专家服务，服务商会更多地考虑成本因素，即随薪酬的提高选择较低能力的专家，尽管此决策会造成服务成功率的下降。此外，薪酬是决定服务类型的重要因素，对超值服务而言，薪酬水平的提高可能会导致服务类型转变为普通服务，使得顾客足够多情境下的专家选择标准发生改变。

(4)服务优化能够使专家的能力得到更充分的发挥，提升系统服务能力，但不同需求情境下其发挥作用的方式存在差异。当潜在需求较小时，服务优化不能提高有效需求，但可以使服务商选择较低能力的专家，在降低服务成本的同时提高服务成功率；当潜在需求足够大时，服务优化不影响专家选择，但是可以提高服务成功率与有效需求，从而使服务商获取更大收益。