历史中的数学趣闻轶事

陈晓靓

数学的发展贯穿于整个人类的发展史，每一个时期都有许多伟大的数学家做出了巨大的贡献。现如今，这个多彩的世界到处呈现着数学的痕迹，只要我们学会用数学的眼光观察世界，就会发现数学就在我们身边。我们即将学习的初中数学分为代数、几何、统计、概率等几大板块，而在数学的发展历史过程中，有很多与此相关的经典故事发生。

一、以符代数，由算术到代数

从算术到代数，可划分为三个历史阶段，花拉子米、丢番图、韦达这三位数学家就是相应的标志性人物。阿拉伯数学家花拉子米，写了一本书《还原与对消的科学》，这本书后来叫做《代数学》。还原就是解方程中的“移项”，对消就相当于“合并同类项”。但是花拉子米时代是“文辞代数”的阶段，非常容易产生歧义，而且比较繁琐。到了古希腊数学家丢番图时代，他用音节首字母缩写来表示数，开创“缩写代数”的时代，比如数学中“meter”，就是“米”的意思，缩写就是“m”。不过，历史上第一个有意识、系统地使用字母的是法国数学家韦达。他用统一的字母表示未知量、已知量及其运算，是对传统代数的突破，用字母表示数是由小学算术跨越到初中代数的桥梁。

二、达·芬奇的几何密码

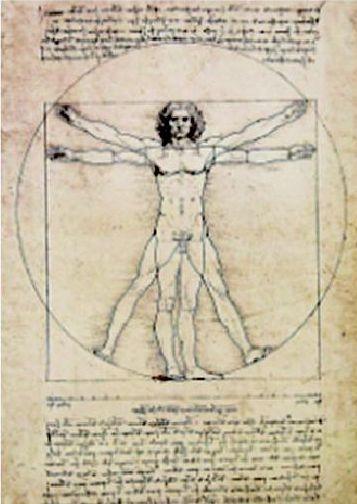
关于达·芬奇的密码，我们得从他的名画《维特鲁威人》说起，这幅画为我们构造了一个美妙的几何世界。这张素描画手稿中一个面对我们的健壮中年男子，两臂微斜上举，两腿又开，以他的头、足和手指各位端点，正好外接一个圆形。同时在画中叠加着另一幅图像：男子两臂平伸站立，以他的头、足和手指各为端点，正好外接一个正方形。这幅画中隐藏着完美的人体比例和黄金分割。如果从脚底量到头顶，从张开双臂的左手量到右手，那么你就会发现高和宽相等。借助连线，我们能延伸出许多几何图形，可以找到圆形、三角形、四边形、五边形、等边三角形等。

三、统计学家与消失的面粉

战争时期德国物资紧缺，对面包实行配给制。有一个统计学家，怀疑他所在区域的面包师私扣面粉，于是就天天称自己的面包。几个月以后，他找到面包师傅，说：“政府规定配给的面包是400克，因为模具和其他因素，你做的面包可能是398、399克，也可能是401、402克，按照统计学的正态分布原理，这么多天的面包重量平均应该等于400克，可是你给我的面包平均重量是398克。我有理由怀疑是你使用较小的模具，私吞了面粉。”面包师傅随即承认确实私吞了面粉，再三道歉并保证马上更换正规的模具。又过了几个月，统计学家又去找这个面包师傅，说：“虽然这几个月你给我的面包都在400克以上，这可能是因为你没有私吞面粉，但也可能是因为你从面包里特意挑大的给我。同样根据正态分布原理，这么多天不可能没有低于400克的面包，所以我认为你只是特意给了我比较大的面包，而不是更换了正常的模具。我会立刻要求政府检查你的模具。”面包师傅只好当众认错道歉，接受处罚。其实统计学离我们的生活并没有那么遥远，很多时候可以利用统计学解决一些生活中的小问题。

四、将军的勇气

公元1053年（北宋仁宗时期），大将军狄青奉旨征讨叛军。将士们日夜兼程，但由于劳累，士气不振，狄青看在眼里，急在心里。狄青便设坛拜神说：“这次用兵，胜败还没有把握，特此祭拜祈求神靈保佑。”于是他命人搬来一百枚铜币，许愿：“如果把这些铜币扔在地上，字面（铸文字的那一面）全部朝上，那么这次出征定能打败敌人。”狄青将装有一百枚铜币的布袋取出，将铜币全数扔出，结果这一百个铜币的字面，竟然鬼使神差般全部朝上。全军将士欢声如雷，士气大振，狄青迅速平定叛军。身为大将军的狄青何尝不知道：掷一枚铜币，正面朝上还是反面朝上，是个随机事件，正面朝上和反面朝上的可能性相等的，都是1/2;两枚硬币都正面朝上的可能性是1/4;三枚都正面朝上的可能性是1/8……100枚都正面朝上的可能性是（1/2）¹⁰⁰。可见，一百枚钱币都正面朝上的可能性是少之又少，几乎不可能啊。回师时，将士们按原先所约，把钱取下，原来那些铜币两面都铸成了一样的，都是有文字的。对狄青来说，一百个钱币字面全部朝上，是个必然事件，但在别人看来，却是几乎不可能出现的事情。从“不可能”到“可能”、从“随机事件”到“确定事件”，这一切足以显示出大英雄狄青非凡的数学智慧。