改进的直觉模糊加权Heronian几何平均算子及其在徽酒评价中的应用
毕太苗,施明华
(皖西学院 金融与数学学院, 安徽 六安 237012)
集结算子作为信息融合的一种重要工具,是信息科学的重要组成部分。目前已被广泛地应用于人工智能、优化研究、模式识别、图像处理、决策科学等多个研究领域[1]。随着时代的发展,人们所处理的信息往往带有一定的模糊性和不确定性。为此,近年来学者们提出大量的模糊信息集结算子。例如:有序加权平均算子用于集结模糊语言信息[2]、直觉模糊信息[3]、犹豫模糊信息[4];有序加权几何平均算子用于集结不确定语言信息[5]、三角直觉模糊信息[6]、区间犹豫模糊信息[7];优先级加权平均算子用于集结区间直觉模糊信息[8]、中智模糊信息[9]、区间犹豫模糊语言信息[10]。
上述集结算子假定信息集结过程中变量间是相互独立的,而这一假设在实际操作中较难满足。目前文献大多使用Bonferroni平均算子和Heronian平均算子,对关联程度较高的信息进行融合。文献[11]将Bonferroni平均算子用于犹豫模糊语言信息的集结,并用于解决智慧医疗卫生系统中的多属性决策问题;文献[12]将Bonferroni平均算子用于生产库存模型中的直觉模糊信息集结;文献[13]进一步提出直觉模糊Bonferroni几何平均算子,并用于求解金融投资中的多属性决策问题。Heronian平均算子和Bonferroni平均算子一样能捕获变量之间的关联性,但其计算量却要明显少于Bonferroni平均算子,近年来受到广泛的关注。文献[14]结合几何平均算子和Heronian平均算子,提出了直觉模糊Heronian几何平均算子和直觉模糊加权Heronian几何平均算子;文献[15]对犹豫模糊语言加权Heronian几何平均算子进行定义,并给出一种多属性决策问题的求解方法;文献[16]给出了区间直觉模糊加权Heronian几何平均算子,并用于电子政务绩效评价的多属性决策问题;文献[17]将Heronian几何平均算子引入语言环境下,定义了不确定语言加权Heronian几何平均算子。但这些加权Heronian几何平均算子在权重相相等时无法退化为Heronian平均算子,并且不满足幂等性。
近年来随着我国人民生活水平的提高,白酒行业得到快速发展。行业龙头川酒、贵酒稳居领导地位,而处于第二梯队的徽酒、鄂酒、苏酒成为白酒行业的生力军,市场占有率不断扩大,品牌辨识度逐渐提高。以古井、口子窖、高炉家酒、迎驾贡酒、皖徽酒等“五朵金花”为代表的主流徽酒品牌,在中部地区有一定的市场影响力,近些年,依托其有效的营销模式和清晰的市场定位,让徽酒在市场中取得了不错的突破,徽酒开始由曾经的地域性品牌向全国性品牌强势迈进。口子窖首启的“盘中盘”营销策略,将重点放在核心消费者终端,取得了空前成功,有效开发和带动了市场消费,品牌市场份额也得到大幅度提高。其后,该模式被其他徽酒企业效仿,也取得了不错的业绩。创新的营销模式和有效的品牌策略,使徽酒在全国白酒市场逐渐站稳脚跟。但随着越来越多白酒企业对这种营销方式的效仿和跟进,市场竞争也在不断加剧,导致各品牌抢夺市场酒店、餐饮等终端消费者的成本不断攀升,而效果却在减弱,导致企业利润大幅度降低。徽酒这种同质化的营销策略很难使其在未来发展中取得有效突破。从长远来看,企业将营销方向从过度关注产品、渠道促销等方面转向品牌运营,才能形成自己的核心竞争力,向良性发展之路迈进。另一方面,随着消费升级趋势的加快,人们的消费理念也在改变,他们开始追求健康饮酒、理性饮酒以及酒企背后的品牌文化。对于白酒企业来说,紧跟时代发展,打造鲜明的品牌,提供个性化、功能性产品才是大势所趋。因此,对于徽酒进行评价,可以找出对徽酒品牌的影响因素,让酒企更加清楚地了解自身的品牌现状,从而进行改进提升,对其未来的品牌发展战略有着至关重要的意义。
综上所述,本文同时考虑到直觉模糊集理论能更好地处理复杂系统中的模糊性和不确定性,对加权Heronian几何平均算子进行重新设计,提出一种改进的直觉模糊加权Heronian几何平均算子,并证明新算子具有退化性、幂等性、单调性、有界性等良好性质,最后,将其用于解决白酒评价的多属性决策问题。
1 预备知识
1.1 直觉模糊集
定义1[3]设X是一给定论域,则X上的一个直觉模糊集A为
其中μA(x):X→[0,1]和υA(x):X→[0,1]分别代表A的隶属函数和非隶属函数,并且∀x∈X有0≤μA(x)+υA(x)≤1.
为便于计算和讨论,将直觉模糊集中的元素用有序区间对α=(μα,υα)表示,并称为直觉模糊数。设α=(μα,υα)和β=(μβ,υβ)是2个直觉模糊数,规定:
1)α⊕β=(μα+μβ-μαμβ,υαυβ);
2)α⊗β=(μαμβ,υα+υβ-υαυβ);
为对直觉模糊数α=(μα,υα)和β=(μβ,υβ)进行排序,Chen等人提出得分函数[18](P13-18),[19]:sα=μα-υα;Hong等人引入精确度:hα=μα+υα;Xu等人将二者相结合,给出如下的排序方法[20]:
· 若sα>sβ,则α>β;
· 若sα=sβ,则
(ⅰ) 当hα=hβ时,有α=β;
(ⅱ) 当hα>hβ时,有α>β.
1.2 Heronian几何平均算子
定义2[14]设p≥0,q≥0,且p与q不同时为0,αi=(μαi,υαi) (i=1,2,…,n)为一组直觉模糊数,若
则称IFGHMp,q为直觉模糊Heronian几何平均(GHM)算子。
但上述Heronian几何平均算子仅考虑了变量间的关联性,忽略了权重信息。为此,Yu等人进一步给出如下定义[14]。
定义3[14]设p≥0,q≥0,且p与q不同时为0,αi=(μαi,υαi) (i=1,2,…,n)为一组直觉模糊数。若
则称IFWGHMp,q为直觉模糊加权Heronian几何平均(IFWGHM)算子。
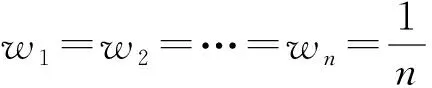
2 改进的直觉模糊WGHM算子

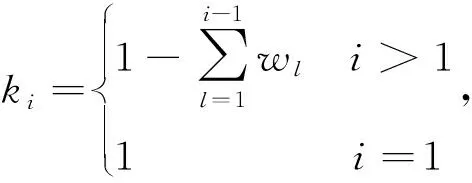
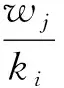


进而有
(1)
故有
下证,由IIFWGHM算子的集结值是直觉模糊数。
由0≤μαi≤1,0≤υαi≤1,易知
和
又
综上定理得证。
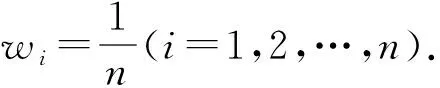
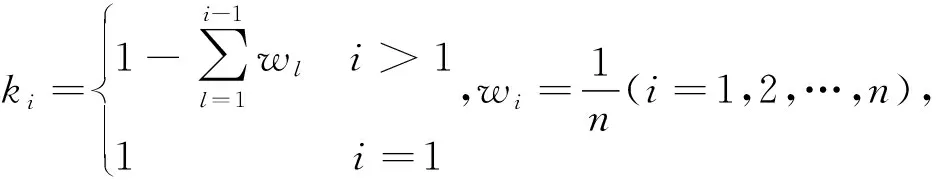
因此
定理3(1) (幂等性)αi(i=1,2,…,n)为一组直觉模糊数,若αi=α(i=1,2,…,n),则有
(2) (交换性)αi(i=1,2,…,n)为一组直觉模糊数,若α′1,α′2,…,α′n为α1,α2,…,αn任一置换,则有
(3) (单调性)αi=(μαi,υαi),βi=(μβi,υβi)(i=1,2,…,n)为两组直觉模糊数,若对任意的i=1,2,…,n,都有μαi≤μβi,υαi≥υβi,则
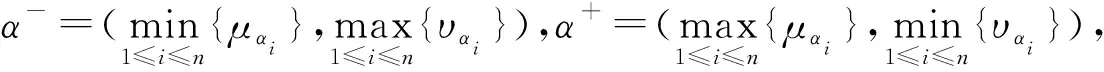
证明:(1)
(2)
(3) 因为μαi≤μβi,υαi≥υβi(i=1,2,…,n),故有
从而
同理可得
所以
不妨设IIFWGHMp,q(α1,α2,…,αn)和IIFWGHMp,q(β1,β2,…,βn)的得分函数和精度分别为sα、sβ以及hα、hβ,则由上式得sβ≥sα.
1) 若sβ>sα,则直接可得
IIFWGHMp,q(α1,α2,…,αn)
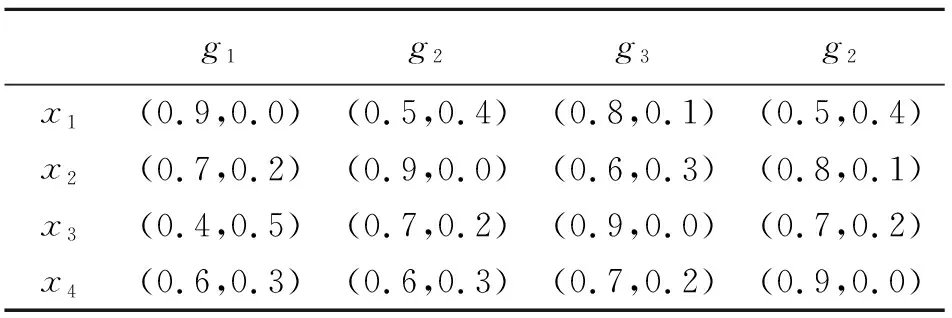
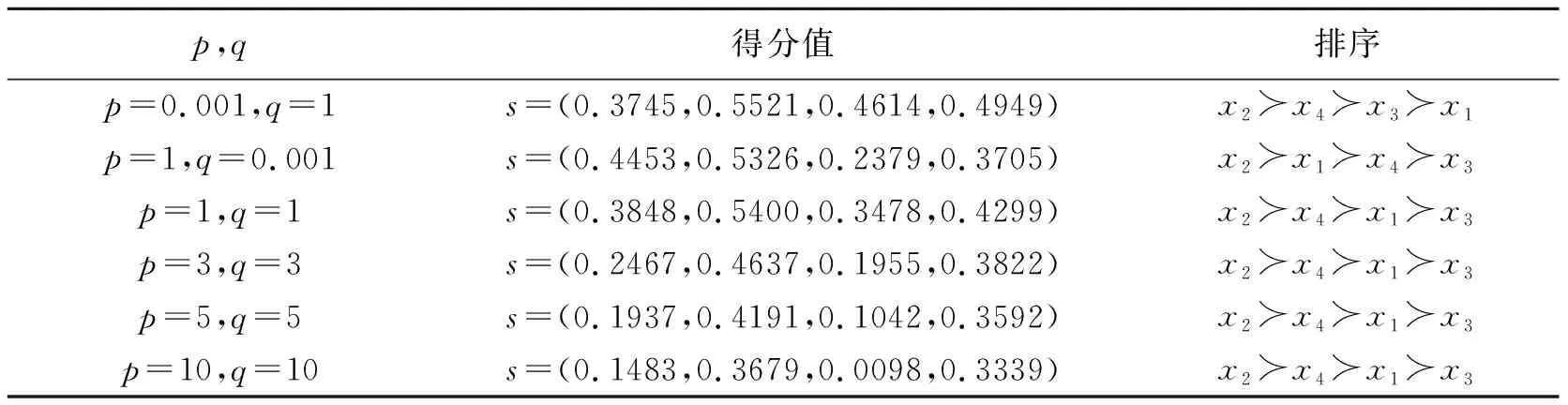
2) 若sα=sβ,结合μαi≤μβi,υαi≥υβi(i=1,2,…,n),可得 和 从而有hα=hβ,因此 综上,(3)成立。 (4) 由(1)和(3)可得 和 即 综上,定理3得证。 下面我们给出IIFWGHM算子的一些特殊形式。 情形1若p=0, 则有 情形2若q=0, 则有 情形3若p=1,q=1,则有 注:1) 由情形1和2可知参数p,q不具备交换性,即 2) 当q=0时IIFWGHM算子无法捕获变量的权重信息。 在前文定义的IIFWGHM算子基础上,给出上述决策问题的求解步骤,具体如下: 步骤3:依次计算上述综合评价值的得分值(如需要,则进一步计算精度值),利用方案综合评价值的得分对决策方案进行排序,并选择最优方案。 假定某公司打算选择某徽酒品牌进行投资,经过前期的市场调研,4种徽酒品牌(x1,x2,x3,x4)进入备选。智囊团的成员决定从以下4个因素(对应的权重为w=(0.2,0.3,0.3,0.2)T),对各4种徽酒品牌的进行评估: g1-支持力,指的是品牌受关注度和社会的认可度,具有强大支持力的品牌在市场中的传播力度更加强劲,而且能够获得较强传播投资和营销支持; g2-市场力,指的是品牌在市场中的占有率。一个具有较大市场占有率的品牌,在市场中的认知度会明显优于其他品牌,竞争优势也增强; g3-行销范围,指品牌的销售区域,拥有较强的跨区域、跨文化传播的能力。若该品牌行销范围广,则在市场更具有认知度和声望; g4-趋势力,指的是品牌是否能与企业未来发展相契合,具有良好趋势力的品牌能够顺应市场的发展,抓住消费者的需求和变化,并与之保持同步。 最终,专家组达成一致评价意见,并给出如下的直觉模糊信息评价矩阵。 表1 直觉模糊信息评价矩阵 为选择最佳建设方案,下面利用本文的决策方法进行求解,具体步骤如下: 步骤1:题中涉及的属性均为效益型指标,因此无须规范化,可直接进行优选决策; 步骤2:利用IIFWGHM集结算子对上述评价矩阵第i行进行集结,得到方案的综合评价值,具体如表2。 表2 IIFWGHM算子集结结果 步骤3:计算各徽酒品牌综合评价的得分值,并据此进行排序(如表3所示),为公司选择最佳投资品牌。 从表3可见p,q取值不同时,尽管最佳选择是x2,但整体排序却不一致。由此可知,IIFWGHM算子决策方法依赖于参数取值,考虑到计算复杂性等因素,一般情况下建议决策时取p=q=1。从表2以及表3我们还可以见到一个有趣的现象,当p,q取值相等时,参数取值越大,评价值和得分值越低。事实上,可以证明p=q时,IIFWGHM算子是关于参数递减的,对于乐观者可以选择取值较低的参数,而悲观者则相反。但过大的参数也会导致模型识别能力降低,例如本题中p=q=30时,x2~x4~x1≻x3.因此决策过程中要合理的选择参数进行决策。 表3 决策结果 下面我们将本文方法同已有的直觉模糊多属性决策方法进行对比,由于这些方法的主要区别在于使用不同的集结算子,因此我们有重点的选取直觉模糊加权Heronian平均(IFWHM)算子[21],直觉模糊加权几何Heronian平均(IFWGHM)算子[14],以及直觉模糊加权Bonferroni平均(IFWBM)算子[22],同本文的改进的直觉模糊加权几何Heronian平均(IIFWGHM)算子进行对比,具体结果如表5所示。 表4 方法比对结果 在经济社会快速发展的今天,人们所面临的信息往往具有一定的不确定性和模糊性,直觉模糊数是处理此类信息的一种有效技术。本文对于现有的加权几何Heronian平均算子进行设计,给出了一种具有退化性以及幂等性等优良性质的直觉模糊加权几何Heronian平均算子。此外,基于新设计的算子,提出一种多属性决策方法,徽酒品牌评价案例表明方法的可行性和有效性。3 直觉模糊多属性决策方法
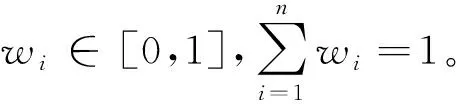
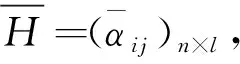
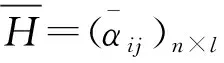
4 实例分析

5 比较分析

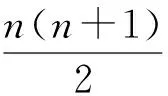
6 结论

