基于正余弦算法和误差修正组合方法的汇率预测研究

刘文正，曹文秀，樊昊煜

基于正余弦算法和误差修正组合方法的汇率预测研究

刘文正，曹文秀，樊昊煜

（兰州交通大学 交通运输学院，甘肃 兰州 730070）

针对汇率数据具有高波动性、非线性和高噪声等特点，提出了一种基于分解算法和误差修正的汇率时间序列预测方法（VMD-SCA-ELM-EC）。该方法首先利用变分模态分解（VMD）算法对原始数据进行分解，然后采用正余弦算法优化的极限学习机神经网络（SCA-ELM）对各个分量进行预测，并采用误差修正法（EC）拟合误差因素，最后将各项预测结果进行线性集成。选择英镑兑美元每日汇率序列进行分析预测，并将提出的模型与多种常见预测模型进行对比，实证分析得出，该方法在一步和多步提前预测中均取得更优的预测精度和方向准确率。

汇率预测；多步预测；正余弦算法；极限学习机；变分模态分解

引言

汇率稳定是国家经济稳定的体现，也是国家综合实力的体现。汇率不仅影响着各个国家的进出口贸易和物价的稳定，也是各个国家在政治和军事影响力为达目的的金融手段。汇率的准确分析和预测，对国家制定相应的金融政策、企业妥善的规避金融风险以及个人合理的理财投资都具有深远的影响。然而，汇率的高波动性、非线性和高噪声等特征，给汇率的精确、稳定预测带来了极大的难度。此外，汇率受到多种外生因素的影响，造成影响因素特征选择和提取的困难，导致预测精度和稳定性的波动。因此，近几年，汇率预测已经成为国内外学者重点研究课题之一。

目前，从国内外对汇率预测研究来看，已取得较大的进展。汇率预测的方法主要可以分为传统经济计量和统计方法、单模型方法和组合模型方法这三类。传统经济计量和统计方法，主要有ARMA模型[1~2]、GARCH模型[3]等，此类模型在长期预测中可以取得较高的预测精度，但已有的研究表明，在短期预测汇率中很难准确分析其波动性，导致预测误差较大，很难获得预期效果。为解决复杂度高和非线性等特征问题，人工智能技术得到了广泛的应用，对数据趋势的捕捉和预测精度的提高取得了较大的进展。其中，单模型方法，主要有神经网络[4]、支持向量机（Support Vector Machine，SVM）[5]和深度学习技术[6]等。金艳凤[4]采用BP神经网络对人民币兑美元汇率进行预测分析，研究结果表明，BP神经网络易出现“过拟合”现象，附加动量的BP算法具有更优的预测效果。阿磊[5]对自回归模型和SVM进行对比研究发现，SVM具有更优的预测效果，但对其参数选择和优化的难点并未提出解决方法。晁静[6]通过对三种汇率的预测研究，采用深度信念网络（Deep Belief Networks，DBN）得到了收敛至全局更优的预测结果，相对于前馈神经网络，该方法克服了易陷于局部极小值的缺陷。这些方法在短期预测中对非线性时间序列有较好的拟合效果，因此对汇率预测的精度有较大的提高，但此类方法由于较为单一，预测精度的稳定性很难获得保证。为提升预测稳定性，常采用优化和分解等组合模型方法，常见的有分解算法[7~11]、优化算法[12]和经济计量模型[13~15]分别和神经网络结合的组合模型。谢赤等[6]首先采用经验模态分解（Empirical Mode Decomposition，EMD）算法对人民币兑美元汇率原始序列进行分解，充分提取原始数据中的信息，再通过Elman神经网络进行预测，得到了较优的预测效果。惠晓峰等[12]利用遗传算法优化的BP神经网络获得了更稳定、更准确的预测效果，且研究结果表明优化算法对预测模型有较大的提升。毛舟[15]采用ARIFMA模型、SVM

模型和BPNN模型通过非线性函数构建的组合模型，相对于单一模型，这种组合方式可以较为准确捕捉短期汇率走势，获得更优的预测结果。上述组合方法进一步提升了神经网络方法预测结果的精确性和稳定性，徐卓顺等[16]也在研究中通过对比单一模型和组合模型发现预测波动性复杂的数据时，组合模型预测效果更好。然而，在对汇率预测研究中，很少有学者将误差因素考虑到组合模型中。Yu等[17]在对时间序列预测中通过加入误差因素构建的组合模型，预测效果得到了进一步提升，并且研究结果表明，预测误差序列中仍包含原始数据的信息，如果对误差进行预测修正，可进一步提升预测精度。因此，本文将误差因素考虑到预测汇率时间序列中，对汇率数据通过分解、预测和误差修正法（Error Correction，EC）进行研究和分析。

鉴于上述研究，本文提出了一种基于分解算法、优化算法和误差修正法组合的汇率预测方法。该方法通过分解算法对原始汇率序列进行分解，将分解后的各个分量采用正余弦算法（Sine Cosine Algorithm，SCA）优化的极限学习机（Extreme Learning Machine，ELM）神经网络进行预测，以及将预测误差序列进行误差修正，最后将各项预测结果线性集成获得最终预测结果。

1 预测模型

1.1 变分模态分解

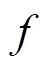
1.2 正余弦算法

正余弦算法（Sine Cosine Algorithm，SCA）[19]是Seyedali Mirjalili在2016年提出的一种基于正弦和余弦函数的元启发式算法，因其原理简单、易于实现和收敛速度快等优点，广泛应用于各个领域。正余弦算法在寻优过程中主要可以分为探索和开发两个阶段，这两阶段分别对应全局寻优和局部寻优。在前一阶段，随机快速搜索空间中的可行区域；后一阶段，在可行区域内寻找可行解，这一阶段搜索效率会低于前一阶段。在搜索和开发的过程中，是通过使用正弦或余弦函数更新下一次寻优的方向和位置，具体表达式如下：

图1 正余弦算法寻优搜索过程

正余弦算法通过上述寻优机制，在探索阶段可以快速地找到全局最佳区域，避免陷入局部最优，且在运算过程中，近似的全局最优位置会被存储作为目标点，以便开发阶段进一步搜索。在开发阶段，搜索过程会围绕最佳区域进行局部搜索，逐步收敛于最优解。

1.3 极限学习机

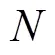
极限学习机神经网络的拓扑结构如图2所示，该算法只需设定隐含层神经元个数，在训练过程中随机产生输入层和隐含层之间的连接权值和阈值，且无须调整，即可获得唯一最优解，因此具有学习效率高、泛化性能好等优点。

图2 极限学习机神经网络拓扑结构

1.4 VMD-SCA-ELM-EC模型

ELM神经网络在进行预测时，由于其输入层和隐含层之间的连接权值和阈值是随机产生的，这就导致预测效果不稳定，通常研究者会采用优化算法对连接权值和阈值实现优化。因此本文采用SCA优化ELM神经网络（SCA-ELM）输入层和隐含层的连接权值和阈值，起到预测结果稳定的效果。由于汇率具有非线性和高噪声的特征，在预测时噪声会对预测产生影响。因此需要首先对原始数据采用VMD算法进行分解，以此来消除噪声的干扰。然后再用SCA-ELM对各个分解分量进行预测，并获取每个分量的预测值。但往往因为预测器在对数据进行拟合时会对造成一定的偏差，导致数据中部分有效信息无法捕捉，所以误差修正是提升模型效果的有效工具。因此，再次采用SCA-ELM预测误差以达到对过去误差中出现的有效信息的捕捉，以拟合未来预测结果中可能会缺失的有效信息。最终结果由各分量预测结果和修正的误差线性集成获得。如图3所示，该组合模型的具体流程如下：

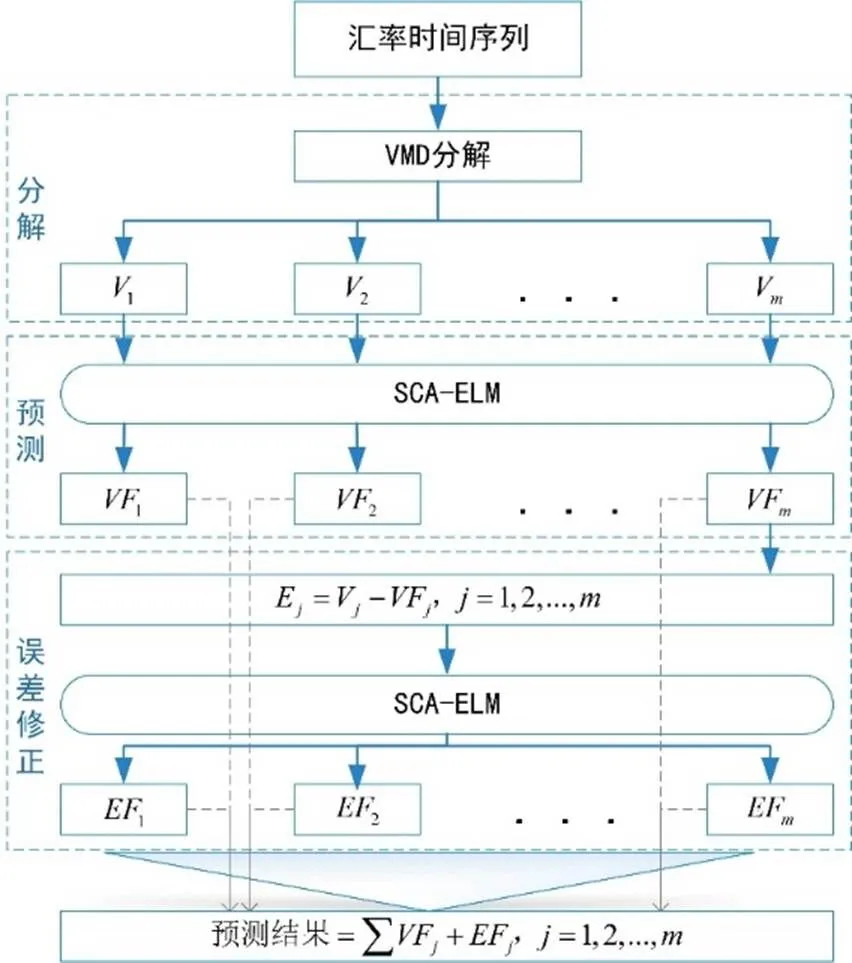
图3 VMD-SCA-ELM-EF模型流程

步骤1：在获取EEMD算法分解个数的基础上，设定VMD分解个数的范围，然后根据VMD-SCA-ELM模型预测效果的优劣，采用试错法最终确定VMD算法的分解个数，并对原始数据进行分解。

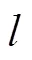
步骤3：根据SCA的目标函数值，自动地选取合适的ELM神经网络连接权值和阈值，并对各分解分量进行预测。

步骤5：对各分量预测结果和各误差修正序列进行线性集成，获得最终预测结果。

以上5个步骤为模型的具体流程，在实验过程中，首先需对数据划分为训练集和测试集；然后对训练集进行上述5个步骤，以拟合最佳模型和参数，并将模型保存；最后在测试集对训练出的模型进行验证，以证明模型的有效性和优越性。

2 实证分析

2.1 实验数据和参数选择

本文选取2012年1月2日至2017年12月29日在外汇市场中英镑兑美元（GBP/USD）每日汇率作为样本数据，共1559个数据，对每日汇率走势进行预测和分析，具体走势如图4所示。

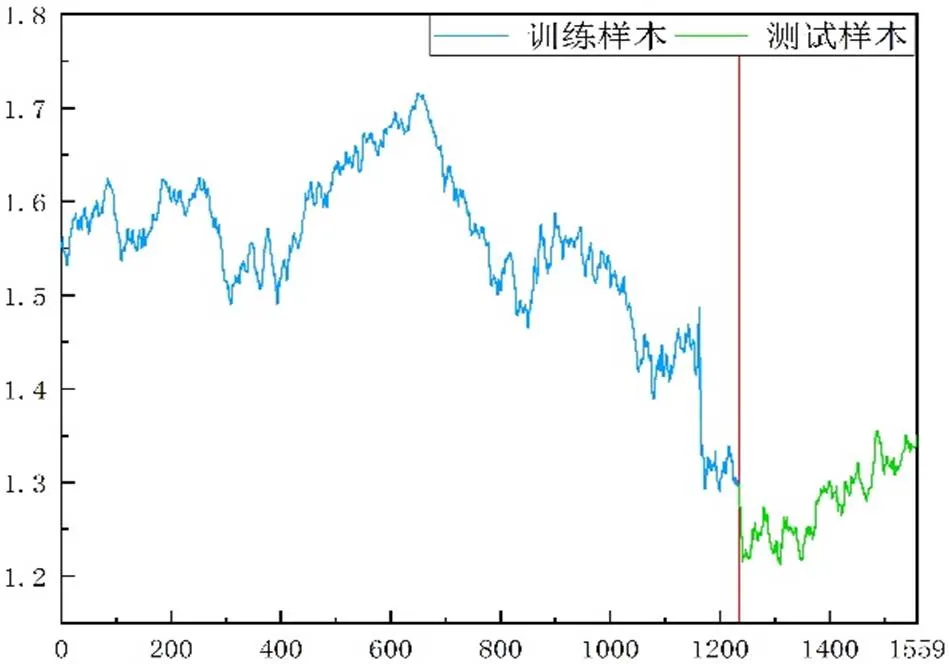
图4 GBP/USD汇率时间序列

在预测时，将2012年1月2日至2016年9月30日共1234个数据作为训练样本；将2016年10月3日至2017年12月29日共325个数据作为测试样本。样本数据的统计性描述如表1所示，从表中可知，GBP/USD汇率数据偏度不等于0，且峰度不等于3，说明数据不服从正态分布，波动性大。

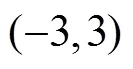
表1 GBP/USD汇率数据的统计描述

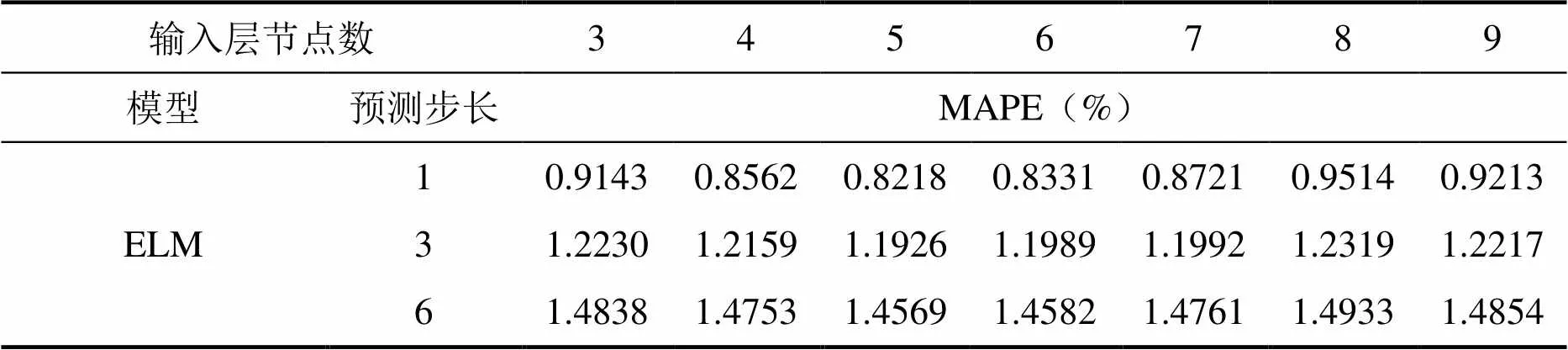
表2 ELM输入层节点个数确定

表3 VMD分解个数确定

此外，为了验证本文提出的VMD-SCA-ELM-EC组合模型有效地提升了预测精度，本文还采用粒子群算法（Particle Swarm Optimization，PSO）优化ELM模型（PSO-ELM）、SCA-ELM模型、EEMD-SCA-ELM模型和VMD-SCA-ELM模型分别预测了GBP/USD汇率序列。通过与上述对比模型比较，可以进一步验证组合模型中VMD算法、SCA算法和误差修正法对模型的预测精度和稳定性提升的效果。此外，本文对原始数据进行了一步、三步和六步提前预测，进而验证所提出的模型不仅在一步提前预测中有较优的效果，而且在多步提前预测中仍能保证较高的预测精度。

2.2 模型评价与对比

为了能使所提出的组合模型与其他对比模型比较，本文从预测误差和方向两个方面对所有模型预测结果进行综合评价。本文选择了平均误差百分比（MAPE）、均方根误差（RMSE）和方向准确率（DS）这三种评价标准，具体公式如下：

本文提出的模型和对比模型的预测性能比较的详细数据见表4，及一步、三步和六步预测结果分别见图6，图7和图8。由表4误差分析和图6，图7和图8预测结果对比可知，VMD-SCA-ELM-EC模型的MAPE值和RMSE值，不仅在一步提前预测效果低于其他对比模型，而且在多步提前预测中预测结果的精确性也更优。在一步提前预测的MAPE值中，提出模型相比于其他模型分别提升了69.53%、36.81%、31.42%、4.89%和0.37%。此外，根据方向准确率（DS）来看，在一步和多步提前预测中，本文提出的模型也对样本数据未来走势有较为准确的预测。综上所述，从预测精度和方向准确率两个方面，本文提出的模型均优于其他对比模型。

表4 各个模型误差分析结果

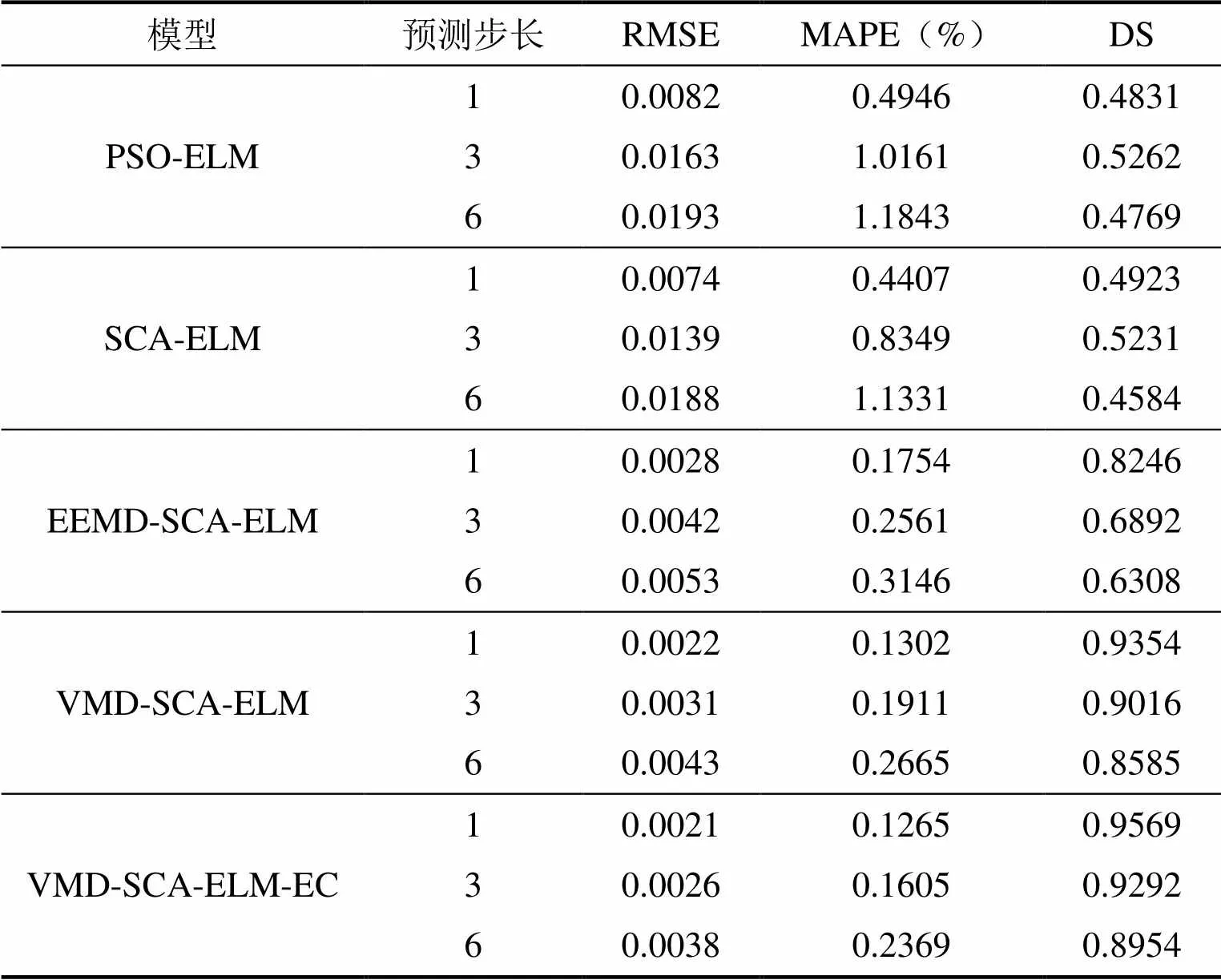
表4 各个模型误差分析结果（续）

本文提出的组合模型的优越性主要是由于以下几个方面的原因：第一，单模型ELM神经网络与优化后的模型（PSO-ELM和SCA-ELM）相比，在数据拟合中，对ELM模型权值和阈值初始化的优化有效地提升了模型拟合效果。在一步提前预测MAPE值中，优化算法对模型精度提升了约30%；在多步提前预测MAPE值中，优化算法对模型精度提升了约20%，因此优化算法提升了模型的预测效果。第二，PSO-ELM模型和SCA-ELM模型的预测结果对比说明SCA算法对ELM神经网络的权值和阈值优化效果要优于PSO算法，在一步和多步提前预测MAPE值中，SCA算法相比PSO算法对模型精度提升了约5%，且在实际训练预测过程中SCA算法搜索优化的效率明显高于PSO算法。第三，相比于仅采用优化算法的模型，分解集成的模型对数据预测提升效果更为明显，具体来看，在一步和多步提前预测MAPE值和DS值中，分解集成模型相比优化的模型分别提升了约30%和45%。由此可看出对数据进行分解预处理，可以有效地降低原始数据的复杂度和预测难度。第四，EEMD-SCA-ELM模型和VMD-SCA-ELM模型预测结果对比表明VMD算法对原始数据分解消除噪声的能力优于EEMD算法，在一步和多步提前预测MAPE值中，VMD算法相比EEMD算法对模型精度提升了约5%。主要是因为VMD算法也有效地抑制了EEMD算法数据分解中常出现的模态混叠和算法效率低的缺点，从而更好地对数据进行降噪分解和挖掘数据隐藏信息，在预测中可对隐藏信息有效的捕捉以模拟未来数据走势。第五，误差修正法的应用是为了应对汇率预测中因模型的缺陷等问题造成数据中有效信息遗漏，导致较大误差的存在，该方法通过对已知误差信息的有效挖掘以模拟出未来预测中可能会出现的误差，从而做到对预测结果精确性和稳定性的进一步提升。

因此，本文提出的VMD-SCA-ELM-EC模型不仅降低了原始数据噪声的干扰，而且对误差中残留的有效信息进行了进一步的挖掘。该模型综合了VMD算法，SCA算法和误差修正法的优势，使得模型在预测精度和方向准确率方面均可以获得较优的效果，所以可以作为一个有效的预测方法在一步或多步汇率预测中广泛应用。

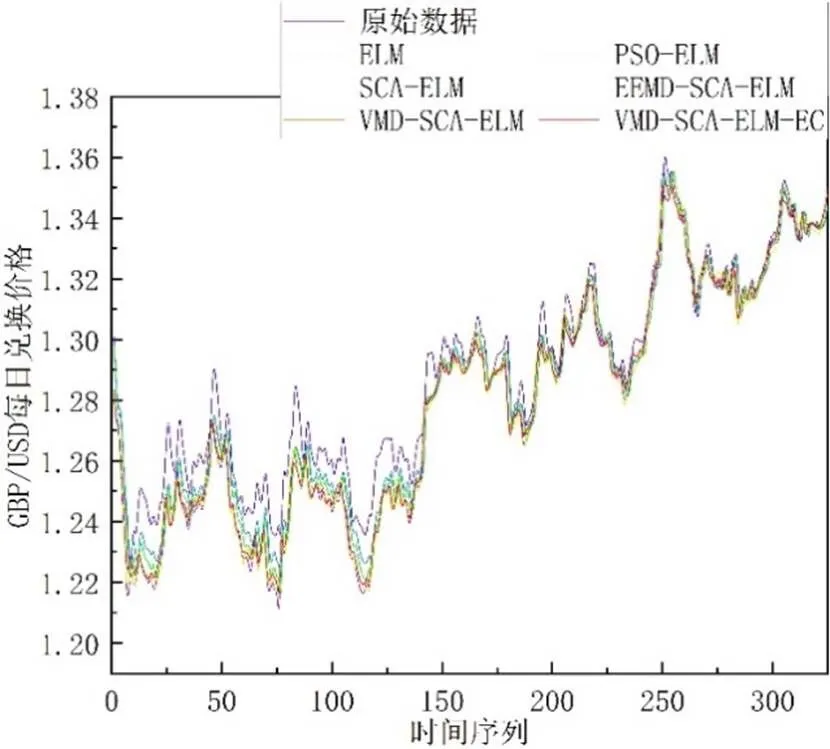
图6 各个模型的一步提前预测结果图

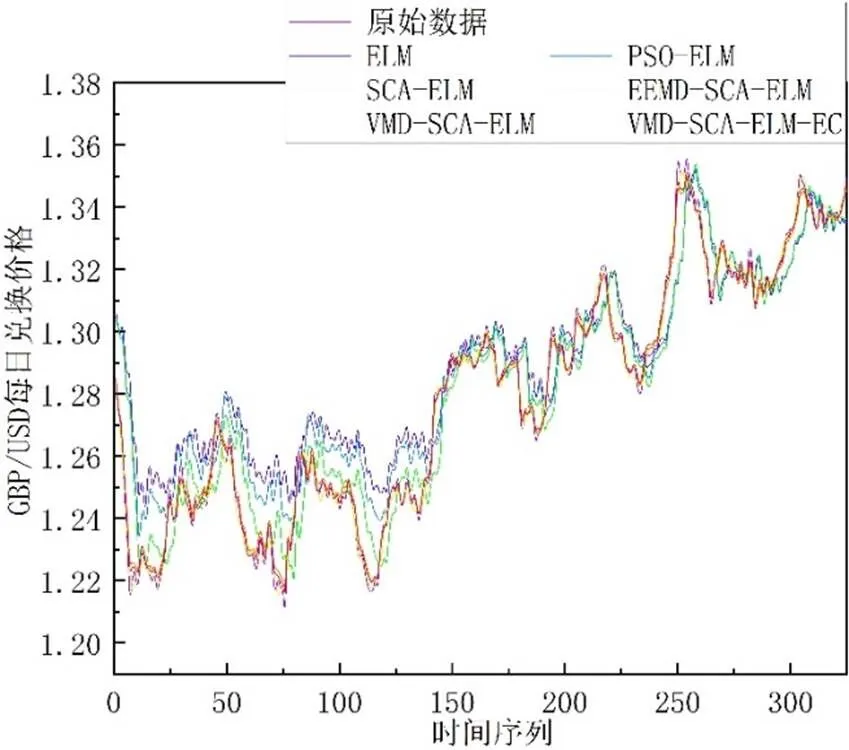
图7 各个模型的三步提前预测结果图

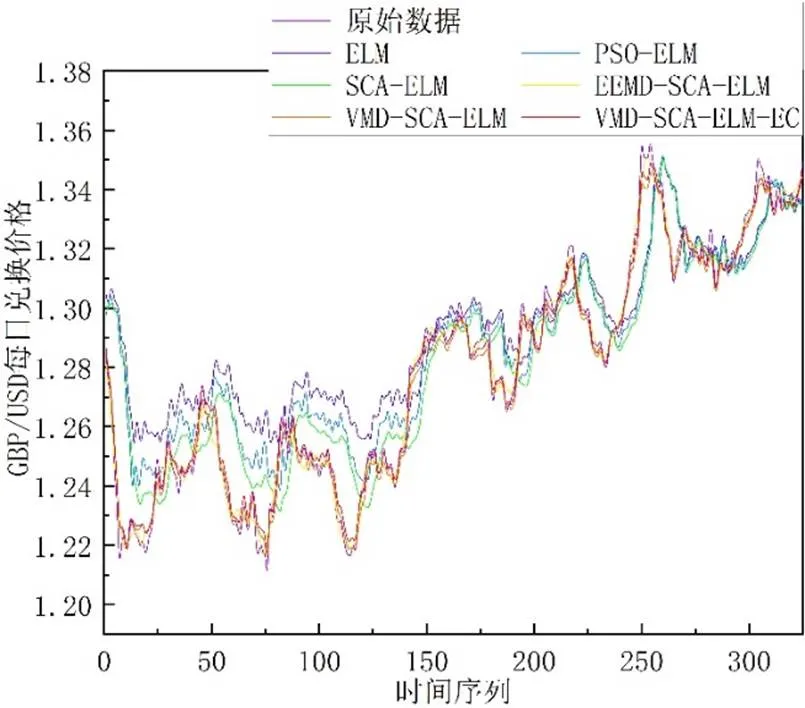
图8 各个模型的六步提前预测结果图

结论

本文提出了基于误差修正的组合模型对英镑兑美元汇率进行了预测分析。在预测过程中，采用VMD算法对原始数据进行分解预处理获得了更好的降噪效果，降低了原始数据的复杂度以及预测难度；SCA作为一种高效的智能算法，优化ELM神经网络的权值和阈值从而提升对数据的拟合效果并提升预测精度。此外，本文在汇率预测中考虑到了误差因素会对预测结果精度有一定影响并且往往有部分有效信息隐藏在误差中，因此，采用了误差修正法进一步多已知误差中的有效信息进行捕捉从而拟合未来预测趋势中可能产生的误差，从而使得预测精度得到进一步提升。实证结果表明，相比于其他常见的预测模型，提出的VMD-SCA-ELM-EC模型能够有效地预测汇率时间序列。该模型在预测精度和方向准确率两个方面都较好，不仅在一步提前预测中结果较优，而且在多步提前预测中仍能保证预测结果的稳定。因此，该模型可以在实际汇率预测中作为一个可用的预测工具，为投资者、管理者和研究者等提供有效的未来走势数据。此外，该模型可对非线性、不平稳和高波动的数据进行有效的拟合，因此也可应用到其他金融预测领域，如股票预测、原油价格预测和期货价格预测等。

[1] 戴晓枫, 肖庆宪. 时间序列分析方法及人民币汇率预测的应用研究[J]. 上海理工大学学报, 2005（4）: 341~344.

[2] Rout M , Majhi B , Majhi R , et al. Forecasting of currency exchange rates using an adaptive ARMA model with differential based evolution[J]. Journal of King Saud University Computer & Information Sciences, 2013, 26(1): 7 ~18.

[3] 惠晓峰, 柳鸿生, 胡伟, 等. 基于时间序列GARCH模型的人民币汇率预测[J]. 金融研究, 2003（5）: 99~105.

[4] 金艳凤. 基于BP神经网络的汇率预测模型研究[D]. 武汉:武汉理工大学, 2013.

[5] 阿磊. 基于支持向量回归机的汇率预测[D]. 上海: 华东师范大学, 2011.

[6] 晁静. 基于DBN的汇率预测研究[D]. 南京: 南京大学, 2012.

[7] 谢赤, 郑林林, 孙柏, 等. 基于EMD和Elman网络的人民币汇率时间序列预测[J]. 湖南大学学报（自然科学版）, 2009（6）: 89~92.

[8] 傅魁, 郭志颖. 基于MEEMD组合模型的汇率预测[J]. 统计与决策, 2018（11）: 77~80.

[9] Das P P , Bisoi R , Dash P K .Data Decomposition based Fast Reduced Kernel Extreme Learning Machine for Currency Exchange Rate Forecasting and Trend Analysis[J].Expert Systems with Applications, 2017, 96: 427~449.

[10] 鱼丹. 基于遗传算法的BP神经网络在汇率预测中的应用[J]. 科学技术创新, 2019（3）: 100~101.

[11] 李振中. 基于小波分析和PSO-WLSSVM模型的汇率预测方法研究[D]. 广州: 华南理工大学, 2013.

[12] 惠晓峰, 胡运权, 胡伟. 基于遗传算法的BP神经网络在汇率预测中的应用研究[J]. 数量经济技术经济研究, 2002（2）: 80~83.

[13] 熊志斌. ARIMA融合神经网络的人民币汇率预测模型研究[J]. 数量经济技术经济研究, 2011（6）: 64~76.

[14] 李明景, 汪金菊. 基于ARMA-稀疏贝叶斯模型的汇率预测研究[J]. 合肥工业大学学报（自然科学版）, 2014（8）: 1019~1024.

[15] 毛舟. 基于ARFIMA-SVM-BPNN非线性组合模型的人民币汇率预测研究[D]. 湖南: 湖南大学, 2015.

[16] 徐卓顺, 赵红强. 人民币兑美元汇率预测的单一和混合模型比较分析[J]. 商业时代, 2014（14）: 73~75.

[17] Yu Z , Yang C , Zhang Z , et al.Error correction methodbased on data transformational GM(1,1) and applicationon tax forecasting[J]. Applied Soft Computing, 2015, 37: 554~560.

[18] Dragomiretskiy K, Zosso D. Variational Mode Decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531~544.

[19] Mirjalili S . SCA: A Sine Cosine Algorithm for solving optimization problems[J]. Knowledge Based Systems,2016, 96: 120~133.

[20] Huang G B , Zhu Q Y , Siew C K .Extreme learningmachine: Theory and applications[J]. Neurocomputing,2006, 70(1~3): 489~501

Research of Exchange Rate Prediction Based on Combinatorial Approach of Sine Cosine Algorithm and Error Correction

LIU Wen-zheng, CAO Wen-xiu, Fan Hao-yu

(School of Traffic & Transportation, Lanzhou Jiaotong University, Lanzhou Gansu 730070, China)

A time series prediction method for exchange rate data (VMD-SCA-ELM-EC) based on decomposition algorithm and error correction is proposed to address the problems of high complexity, nonlinearity and high noise of exchange rate data. The method first decomposes the raw data by using the variational mode decomposition (VMD) algorithm, then predicts each component by the extreme learning machine neural network optimized by the sine cosine algorithm (SCA-ELM), and fits the error factors with the error correction method (EC), and finally linearly integrates the results of each prediction. The daily exchange rate series of GBP/USD is selected for analysis and prediction, and the proposed model is compared with a variety of some common prediction models, and empirical analysis shows that this method achieves better prediction accuracy and directional accuracy in both one-step-ahead and multi-step-ahead.

exchange rate prediction; multi-step prediction; sine cosine algorithm; extreme learning machine; variational mode decomposition

2020-05-14

刘文正（1996—），男，甘肃嘉峪关人，硕士研究生，研究方向：机器学习、汇率研究。

TP18

A

2095-9249（2020）03-0067-08

〔责任编校：范延琛〕