从形美出发向神美迈进——《点阵中的规律》教学实录（二）

魏峰

【教学内容】

北师大版五年级上册第98页。

【教学过程】

一、课前交流

师：今天的数学课就从好玩的图片开始，（如下图）你看到什么了？

（图一让学生通过不同的角度看到两张侧脸和瓶子，图二通过旋转得到不同的人脸）

二、设疑导入

师：你能在10秒钟内说出下面式题的答案吗？

师：同学们是不是觉得这是不可能的事情呢？今天我们就是要把这种不可能变成可能，变成一定能。

三、探求规律

1.引入点阵。

师：（课件出示10×10阅兵实景图）同学们都见过阅兵的场景吗？今天我们学习的图形就隐藏在这些图中，你看这些士兵的队伍排得多整齐，如果把一个士兵看作一个点，那么这个兵阵就变成了一个点阵。这节课我们一起来研究点阵中的规律。（板书课题）

师：这个正方形有点大，我把它变小一点，可以去掉一些点，（边演示边问）去掉了多少？再去掉一些，又去掉了几个点？……

2.探索正方形点阵排列的规律。

●活动一：

屏幕上出现4×4的点阵。

师：现在这个点阵简单多了，你会列式计算出这个点阵吗？

生：4×4。

师：按这样的排列规律，前面一个点阵是什么样的？再前面的呢？看来这组点阵有规律啊，到底有什么规律呢？谁来说一说？

生：这些点阵都是正方形，每行的点数与每列的点数相同。

生：从左往右看，后一个点阵的点数都比前一个点阵的点数多。

师：图中的四个点阵各有几个点？

生：第一个点阵有1×1＝1个点，第二个点阵有2×2＝4个点，第三个点阵有3×3＝9个点……

师：这组算式有什么共同的特点呢？

生：是第几个点阵，每横排就是几个点，算式就是几乘几。

师：那么第五个点阵呢？第十个点阵呢？第n个点阵呢？

（板书：n×n）

小结：刚才我们是横着看每排有几个点和有几排，很快算出了每个点阵中的点子数。是第几个点阵就用几乘几。

●活动二：

师：刚才我们用横线分的方法发现了点阵中的规律，那么能不能换个角度观察和思考，也用一组有规律的算式表示这一组点阵中的点子总数呢？这个任务我们分小组合作完成。

（学生自主或合作探究，教师巡视了解情况）

◆展示交流1：

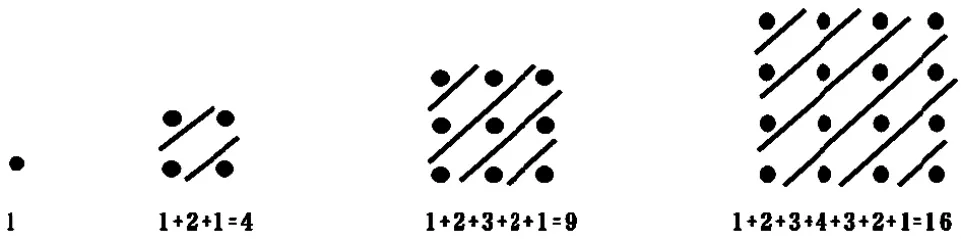
生：我是用斜线划分的。

师：用斜线划分了几个区域？每个区域的点子数是什么样的规律呢？这组算式有什么共同的特点呢？

生：如第二个点阵就从1加到2再加回来，第3个点阵就从1加到3再加回来……

生：就是从1开始，连续的自然数相加，是第几个点阵就加到几，再反加到1。

◆展示交流2：

师：大家还有不同的方法吗？还能换个角度去思考吗？

生：我是用折线拐弯分的。如第二个点阵，用折线把点阵划分了2个区域，点子总数是1＋3＝4。

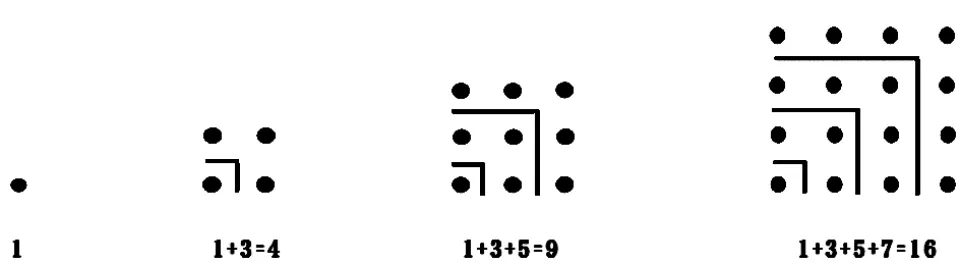
师：第三个点阵呢？

生：点子总数是1＋3＋5＝9。

师：第四个点阵呢？

生：点子总数是1＋3＋5＋7＝16。

师：每个点阵的算式有什么规律呢？

生：都是奇数相加。

师：从奇数几加起？加几个？是随意的几个奇数相加吗？

生：从奇数1加起，连续的奇数相加。

生：不是随意的几个奇数相加。

生：第几个点阵就从1开始加几个连续奇数。

小结：用折线把点阵分为了几个区域，每个区域的点子数都是奇数个，算式都是从1加起，是第几个点阵就加几个连续的奇数。

3.回顾方法。

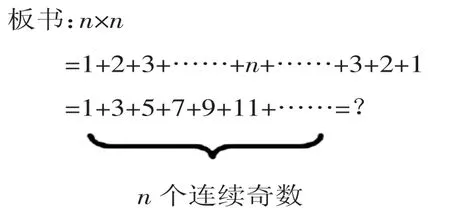
师：（大屏出示点阵图，三种算式）回顾一下，我们一开始是怎样研究点阵的？是化繁为简，从10×10的点阵简化到4×4、3×3、2×2、1×1。我们用横着看、斜着看、折着看三种不同的方法、不同的角度发现了不一样的规律。如果点阵继续增加是不是还会有这样的规律呢？那我们一起试着往后再看一个点阵图好吗？后一个点阵是几乘几呢？

生：横线分，列式为5×5；斜线分，列式为1+2+3+4+5+4+3+2+1；折线分，列式为1+3+5+7+9。

师：为什么三个不同的算式的结果都是25？

生：都是同一个点阵。

师：你喜欢哪一种方法？为什么？

生：我喜欢第一种方法。因为计算简便。

师：这三种算式有什么内在联系？

生：对于算式“1+2+3+4+5+4+3+2+1”我们可以用移多补少的方法变成5个5相加，就是5×5。

生：对于算式“1+3+5+7+9”我们也可以用移多补少的方法变成5个5相加，也是5×5。

师：由于观察的角度不一样，对于同样一个点阵（教师指向第五个点阵），算点子总数：横着看算式是5×5，斜着看算式是1+2+3+4+5+4+3+2+1，折线拐弯看算式是1+3+5+7+9。但结果都是25，还发现三个算式有内在联系，正所谓“横看成岭侧成峰，远近高低各不同，只要移多补补少，大小相等皆明了”啊！

师：第六个点阵你能用三种方法列出算式吗？第九个呢？第n个呢？

四、内化规律

1.10秒钟挑战极限。

师：现在是一开始出现的10×10点阵图。下面的算式你能快速算出结果吗？

1+2+3+4+5+……10+……+4+3+2+1=？

1+3+5+7+9+…19=？

师：你怎么这么快？

生：这两个算式就是我们自己研究的斜着看和折着看的计算方法。

师：10秒挑战还有最后一题，谁来试试？

生：10000。

师：就是几乘几的点阵？

生：100×100的正方形点阵。

师：了不起。看来不可能的事同学们居然做到了，把有规律的算式与点阵建立了联系，数形结合，化难为易，化抽象为形象。数形结合是一种非常重要的数学思想。（板书：数形结合）接下来，我们继续接受挑战吧！

2.下面各点可以摆成正方形的点阵吗？

A：32个点B：36个点C：48个点

D：81个点E：100个点F：1000个点

师：36个点是几乘几的点阵？81呢？100呢？

3.连一连。

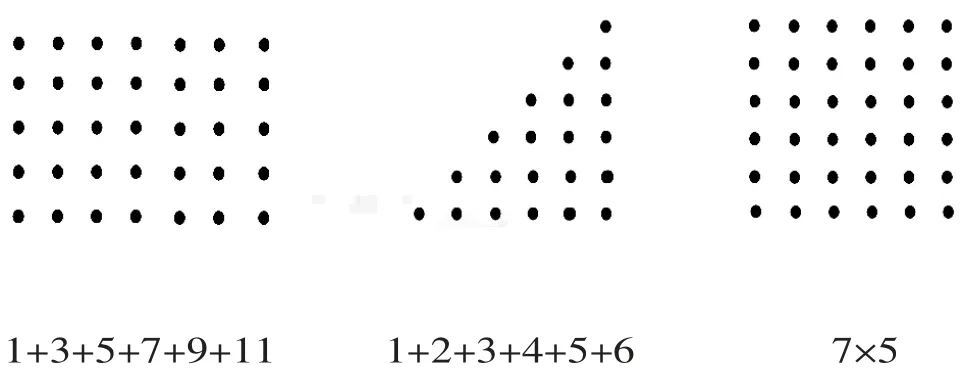
五、总结提升

1.回顾总结。

师：学完本课，有什么收获？

2.拓展延伸。

师：除了刚才我们看到的正方形点阵、三角形点阵、长方形点阵这些平面上的点阵，数学家还将研究领域拓展到空间中。（课件出示以下平面及空间点阵）漂亮吧，可以说点阵应用于生活的方方面面，生活中处处有数学。

师：同学们，我们要学会用数学的眼光去观察世界，用数学的思维去思考世界，用数学的语言去表达世界。