基于AHP灰熵赋权物元分析的矿井火灾风险评价
张九零,孙清清,孙斯维,孙凯杰,宋文静
(华北理工大学 矿业工程学院,河北 唐山 063210)
矿井火灾具有多样性和突变性的特点,受多重因素影响[1],致使火灾判断效率低且耗时长[2,3]。近年来有很多种方法应用于矿井火灾风险评价,如BP神经网络分析、灰色关联度评价、故障树分析、模糊推理与综合评价、基于熵权与突变级数评价等[4,5],上述评价方法应用于矿山火灾危险性评价与多源数据融合分析方面获得了有效的数据结果,但由于理论方法的局限性和处理数据的紊乱特征,导致数据评价与分析过程存在指标权重主观性强、计算处理过于繁琐、样本需求量大和元素相关性低的不足[6]。对此,基于矿井火灾前兆特征与生产过程产生的数据相关性差、结构混乱、价值密度低的特点,将灰熵理论与层次分析法引入至物元可拓理论指标体系中,构建了层次灰熵物元分析的矿井火灾风险评估模型,以实现监测指标数据综合处理,并提高多源数据分析的相关性和融合分析的可操作性[7],避免独立元素权重的客观偏差,高效精准地处理生产过程数据。
1 构建火灾风险评估指标体系
通过搜集文献和对矿山实际的调查结果,构建了矿井火灾风险评估指标体系,如图1。直接因素包括煤的自然倾向[5,8]、煤的破碎状况[5,9]、通风参数[9,10]、煤层物化性质[10];间接因素包括应急处置能力[10]、人员疏散自救能力[7]、明火/隐患的位置[7];管理因素包括技术及管理人员配备[5]、火灾组织协调能力[7,10]、检查评价制度[8,12]、设备隐患整改[10]。其中各评估指标不可分割、相互影响。
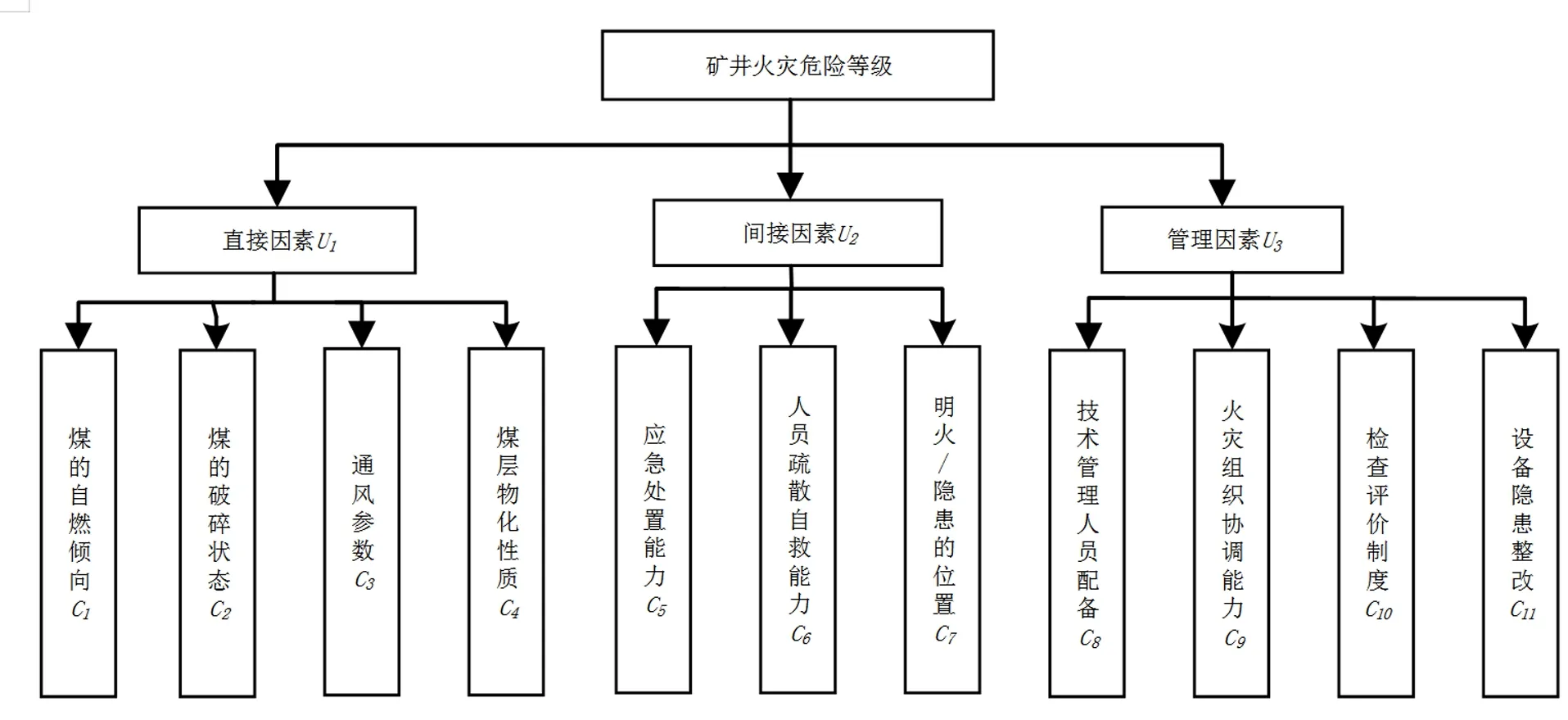
图1 矿井火灾风险评估体系
2 矿井火灾风险评估模型原理
2.1 基于灰熵理论分析指标重要度
运用灰色关联度确定评价指标关联度值,结合指标熵权确定灰熵指数,并依据数值大小进行指标重要度排序。
2.1.1基于灰色关联度确定综合关联系数
(1)灰色绝对关联度ε0i。对特征序列与因素序列进行零像化处理:
(1)
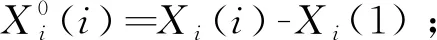
矩阵相关系数为Si:
(2)
灰色绝对关联度ε0i即为:
(3)

(4)
灰色相对关联度γ0i即为:
(5)
(3)灰色综合关联度ρoi:
ρ0i=θε0i+(1-θ)γ0i
(6)
θ为灰色综合关联系数,θ∈[0,1],为平衡起始点变化率的一致程度[4],θ通常取0.5。
2.1.2基于EWM确定灰熵指数
(1)初始数据标准化。初始数据预处理,消除指标间的量纲影响[13]。对获取的m组评估数组、n个评估指标集成初始矩阵X:X=(xij)m×n;初始矩阵无量纲化处理。
越大越优型指标:
(7)
越小越优型指标:
(8)
(2)指标信息熵的计算:
(9)
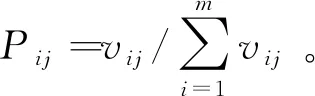
(3)指标熵权的计算:
(10)
式中,dj为指标差异系数,dj=1-ej。
(4)确定灰熵指数
(11)
2.2 基于AHP熵权法确定指标权重
层次分析法对待评指标进行分层定量分析过程中,判断矩阵受经验影响,导致指标权重存在主观偏差[14];运用熵权法综合分析指标信息熵,确定指标权重[15]。计算层次熵权作为指标综合权重,结合了权重分析的主观和客观性,具有较高的可信度[16]。
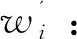
(12)
(2)指标权重。根据得到的相对指标权重计算下层指标权重
AW=λmaxW
(13)
式中,λmax为判断矩阵最大特征根。
(3)修正指标权重:

(14)
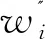
2.3 基于可拓物元模型综合评估危险等级
物元是以事物、特征及特征的量值组成,记R=(事物,特征,量值)=(Z,C,V)。通过特征C的量值范围V对Z进行描述,反映事物的数量关系[17],明确出Z的动态变化。通过层次灰熵构建的矿井火灾评价体系和指标权重体系,结合煤矿安全监察要求,构建安全评价等级体系,并构建评估典域与节域,确定各评价指标与安全等级的关联度,从而通过评价对象综合关联度判断出矿井火灾危险等级。
(1)确定经典域与节域
(15)
式中:Nj(j=1,2,…,m)为划分的第j个危险等级;Ci(i=1,2,…,n)为评价指标;Vji=(aji,bji)为特征指标的量值范围,即一经典域。
(16)
式中:P为全体火灾危险等级;Vpi为特征指标Ci的量值范围,即为节域。
(2)确定待评价物元
(17)
式中:N为待评价对象,Vi待评价指标Ci的值,即为待评价物元。
(3)建立关联函数计算关联度
(18)
式中:Kj(vi)为vi的关联函数,P(vi,Vji)为vi与Vji区间的距离
(19)
(4)计算综合关联度与危险等级
综合关联度表征待评物元P关于等级j的归属程度,且关联度越接近1,相关性越好:
(20)
式中:wi为特征指标Ci的权重系数。
根据贴进度最大原则,评估物元等级:
Kj0(P)=maxKj(P)
(21)
其中:
(22)
(23)
式中:j*为待评区域所属等级特征值。
矿井火灾危险等级判定区域及临界值如表1。

表1 等级判定区间
3 实证分析
3.1 确定待评物元、经典域及节域
通过对唐山市某煤矿企业的危害调查,选取4个采空区煤样进行火灾危险性评估分析。并走访矿井火灾研究领域的7位专家对实地监测的指标体系数据进行百分制评分,并对危险等级划分标准进行修正,最终将矿井火灾危险状态分为5个等级,即Ⅰ级(安全)、Ⅱ级(一般危险)、Ⅲ级(较危险)、Ⅳ级(危险)、Ⅴ级(严重危险),专家对指标数据的评分指标评定数据如表2所示。

表2 指标评定数据
建立经典域R与待评物元R0如式(24)、式(25)所示:
(24)
(25)
3.2 确定待评指标权重
根据实验数据与矿井实际生产状况,通过灰熵理论分析指标评估重要度序列,根据式(9)~式(14)计算得到的C1~C11评价指标灰熵指数分别为:0.774、0.643、0.643、0.527、0.848、0.643、0.913、0.527、0.413、0.579、0.643。指标重要度指数分布如图2所示。
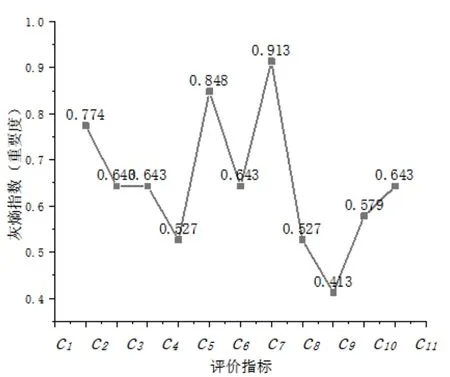
图2 评价指标重要度指数分布
结合评估指标重要度序列,应用层次分析法确定待评指标初始权重,并应用熵权法对检测数据初始权重进行客观修正,确定各指标综合权重,根据式(9)~式(14)计算得到C1~C11待评指标综合权重系数分别为:0.110、0.090、0.090、0.070、0.120、0.090、0.130、0.070、0.060、0.080、0.090。指标权重耦合曲线如图3所示。
3.3 建立关联函数
根据式(18)、式(19)计算出各评价指标与各等级标准区间的关联度。以1#煤样煤自燃倾向分析结果为例,其等级关联度值分别为-0.344、-0.045、0.1、-0.3、-0.475,结合整体指标等级关联度,初步加权求和,依据面积最大化原则即可判断出危险等级为Ⅱ级一般危险。1#样本等级关联趋向如图4所示。
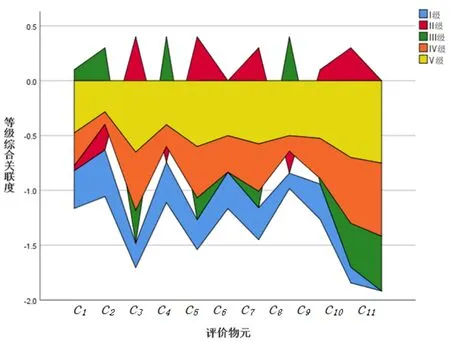
图4 1#样本与各等级关联趋向
3.4 确定综合关联度与危险等级
将评价指标与各等级标准区间关联度值和评价指标权重体系代入式(20)~式(23),计算出评价物元与各等级的综合关联度及所属特征值,评价结果如表3所示。

表3 加权综合关联度及归属等级
3.5 结果分析
经计算得出1#采空区火灾危险性的综合关联度,其分类标准加权关联度K1(P1)、K2(P1)、K3(P1)、K4(P1)、K5(P1)分别为-0.263、0.113、-0.057、-0.388、-0.546,且危险等级特征值为2.329,从而得出1#采空区总体火灾危险程度为Ⅱ级(一般危险)。同理得到2#、3#、4#采空区火灾危险等级分别为Ⅱ级(一般危险)、Ⅱ级(一般危险)、Ⅱ级(一般危险),与煤矿生产实际状况一致,可见该火灾危险性评估方案切实可行。结果与实际状态对比分析如表4所示。

表4 分析结果与实际状态对比
4 结论
(1)将AHP熵权法与可拓理论相耦合,建立了矿井火灾危险等级的评价模型,量化了矿井火灾的危险程度,为火灾防治与救援提供科学、直观的依据。
(2)运用灰熵理论分析对评估指标体系进行重要度排序,为AHP赋值求权提供赋值依据,避免指标赋值的主观性,引入熵权法对指标权重修正处理,融入指标客观权重,使指标权重更加有效、准确。
(3)物元可拓方法可对矿井火灾危险等级进行判断,亦可根据等级归属特征值反映待评目标与危险等级区间的距离,该方法解决了各指标相关性低的问题,其评价结果整体性强且精准有效。
(4)评估方案为矿井火灾危险程度评估提供了一套系统、高效的技术途径,并通过实例验证得出分析结果与实际状态相符,模型实用性强、数据处理高效。煤矿生产企业可根据评价结果采取有效措施定向解决井下生产隐患。

