线性回归分析的R方法

王 晓 刚

(扬州职业大学, 江苏 扬州 225009)

R语言是一种广泛用于统计分析与数据挖掘的、开源而且完全免费的语言,用户可以通过R的网站得到最新版本的R和来自全世界爱好者贡献的近万个用于不同计算的R包及相关使用说明。R操作界面是字符界面,启动后出现R的命令提示符是“>”,用户可以在这里与R交互对话,也可事先建立程序的脚本文件,事后通过菜单“文件运行脚本文件…”运行。虽然在R社区中可以查找到R的几乎所有操作指南,但是信息分散且不成体系。因此，文章针对线性回归分析符合基本假设的情况,借助具体例题,总结在R环境下的回归分析过程。

1 R的基本数据类型与基本运算

有两项操作首先值得一提:一是在菜单“文件改变工作目录…”下改变R的工作目录,这样对工作目录文件之下的文件进行操作时可以不需要指定文件路径;二是可以在菜单“程序包安装程序包…”下安装必要的程序包[1]。

1.1 R的基本运算

在回归分析中,简单的四则运算及开方、指数及对数等运算是必须的,下面列举部分操作示例。

>2+3

#求2与3的和;

>2＾10

#求2的10次方;

>sqrt(1024)

#求1024的算术平方根;

>exp(2)

#求幂e2;

>log(10)

#求ln10。

其中“>”是命令提示符号,“#”是左侧命令的操作或功能说明。

1.2 向量及有关运算

向量是R中样本数据较为常见的组织方式,生成向量的命令函数是c(),“<-”表示赋值,也可用等号“=”表示赋值。以下给出的是向量的生成、向量的常见运算及基本统计指标的计算示例如下：

>x<-c(2.3, 3,5, 7.0, 12, 21.7, 32)

#通过函数c()建立向量并赋值给变量x;

>z=x+y

#向量x与y对应元素相加赋给变量z;

> x*y

#向量x与y元素对应相乘;

>2*x

#向量x每一元素与2相乘;

>x＾2

#向量x每一元素平方;

>min(x)

#求x的最小值;

>mean(x)

#求x的算术均值;

>sd(x)

#求x的标准差;

>a=rbind(x,y)

#以x,y元素为行组成矩阵并赋给a。

1.3 产生有规律的序列

产生有规律的序列也是回归分析过程的常见操作,以下是一些有代表性的示例。

>x=1:15

#产生1到15等差数列,公差为1;

>x=seq(2,15,by=2)

#产生2到15等差数列,公差为2;

>x=seq(from=2,length=8,by=3.2)

#产生首项为2,公差为3.2,项数为8的等差数列;

>x=1:7;logic=x>3

#判别向量x的元素是否大于3,将判别结果赋给逻辑logic。

1.4 数据框及其使用

数据框是R语言的一种数据结构,以矩阵的形式保存数据,但不同的列可以是不同的数据类型。一个数据框相当于关系型数据库中的一张二维表。数据框的建立有两种方法,第一种方法是在命令行上通过函数data.frame()直接生成。由于回归分析的数据量比较大,变量也比较多,一般不用此法。第二种方法是在其它软件中输入数据，或者数据来源本身就是其它软件的输出结果,再读取到R环境中处理。R有多种读取数据文件的方法,其中较为简单而实用的一种为:在较为普及的电子表格软件Excel中输入数据,一个变量占一列,一条记录占一行,将电子表格另存为“.csv(逗号分隔)”文件，如“file.csv”,存储位置选择当前工作目录。下列命令则可以将“file.csv”读取到R中并以数据框的形式赋给数据框变量df。

>df=read.csv(“file.csv”)

需要指出的是,电子表格软件Excel最大行数与最大列数是有限制的。最新Excel 2010版本所允许的最大行号是1048576,最大列号是16384,这样的容量虽然能够满足大部分的应用需求,但也偶有例外,此时可以在“记事本”中将数据文件合并后再在R中读入。

生成数据框后,既可以对某一行整行或某一列整列引用,也可对数据框某一行和某一列交叉点的元素引用。如:

>record2=df[2,] #将数据框df第2条记录赋给变量record2,record2是一个向量;

>variable4=df[,4] #将数据框df中第4个变量的所有值赋给变量variable4,variable4是一个向量。

>height=df[2, 4] #将数据框df第2条记录第4个变量的值赋值给变量height。

2 一元线性回归的R方法

一元经性回归分析包括回归系数估计、假设检验、回归诊断与应用三个部分，现举例说明如下。

2.1 回归系数与假设检验

例1 表1列出了15起火灾事故的损失及火灾发生地与最近的消防站的距离。

表1 火灾损失表

试求直线回归方程并作假设检验。[2]17

将表1在Excel中转置存放,以文件名“file1.CSV”另存为工作目录中。执行下列命令：

>df=read.csv(“file1.csv”)

#读入数据文件,生成数据框df

>x=df[,2]; y=df[,3]

#提取df的两列数据分别赋值给两个向量

>lm.sol=lm(y～1+x)

#执行回归分析命令,分析报告赋给lm.sol

>summary(lm.sol)

#在终端显示lm.sol

>plot(x,y);abline(lm.sol)

#作散点图并作拟合的回归直线见图1

系统输出如下：

Call:

lm(formula=y～1+x)

#模型形式

Residuals:

#残差的五数总括

Coefficients:

#回归系数的估计与显著性概率

Estimate Std.Error tvalue Pr(>|t|)

(Intercept) 10.2779 1.4203 7.237 6.59e-06***

#回归常数的估计与显著性概率

x km 4.9193 0.3927 12.525 1.25e-08***

#回归系数的估计与显著性概率

Residual standard error: 2.316 on 13 degrees of freedom

#残差标准差及其自由度

Multiple R-squared: 0.9235, Adjusted R-squared: 0.9176

#决定系数及修正决定系数

F-statistic: 156.9 on 1 and 13 DF, p-value: 1.248e-08

#回归方程方差分析的F值及显著性概率

结果表明,回归方程是

回归系数假设检验显著性概率与回归方程方差分析的显著性概率均为1.248×10-8,方程具有统计意义。

2.2 回归诊断

对直线回归方程的回归诊断一般包括异常点检测、异方差检验及自相关分析。

2.2.1 异常点检测

例1的异常点检测具体操作如下：

>sre=rstandard(lm.sol)

#提取学生氏残差并赋值给向量sre

>srelogic=abs(sre)>qt(0.975, length(x)-2);srelogic

#根据t分布规律判别异常点,输出TRUE则为异常点

所有点的输出均为FALSE，表明例1样本的15个样本点中,没有异常点。

2.2.2 异方差检验

例1的异方差检验具体操作如下：

>e=residuals(lm.sol)

#提取残差赋值给向量e

>cor.test(x, abs(e),method=“spearman”)

#对自变量x与残差e的绝对值作等级相关分析

结果显示,自变量x与残差e的绝对值之间的等级相关系数仅为0.114,显著性概率为0.686>0.05,说明不存在异方差现象。

2.2.3 自相关分析

在检验直线回归模型是否存在自相关现象,需要在回归分析前对存储数据的数据框的行记录按自变量进行升序排序。例1的自相关检验具体操作如下：

>df=read.csv(“file1.csv”)

>dfo<-order(df [, “距消防站距离x.km.”])

#计算df按x的行记录升序索引号并赋值给向量dfo

>df1=df [dfo,]

#按升序索引排序后的记录赋值给新数据框df1

(1)自相关系数法

>x=df1 [, 2]; y=df1 [, 3]; lm.sol=lm(y～1+x); e=residuals (lm.sol)

>e1=e [1:14]; e2=e [2: 15]

#e1与e2同位号的元素恰是残差向量e前后相邻的两个元素

>cor.test(e1,e2)

#对相邻两点的残差e1与e2作相关性检验

结果显示,相邻两点的残差的相关系数仅为-0.186,显著性概率为0.523> 0.05,说明模型不存在自相关现象。

(2)DW检验

Durbin-Watson检验简称为DW检验,是关于小样本的一种检验方法[3]。对于大样本量,该算法可能无法计算p值。在这种情况下,将打印警告并给出近似p值,该p值是使用具有检验统计量的均值和方差的正态近似计算的。

DW检验的函数是dwtest(),该函数包括在第三方库lmtest中,而且加载该模块时需先首先加载R的时间序列基础库zoo。DW检验法也需要事先对存储数据的数据框的行记录按自变量排序。

>library(zoo);library(lmtest) #加载第三方库zoo与lmtest

>df=read.csv(“file1.csv”);dfo<-order(df [, “距消防站距离x.km.”]); df1=df [dfo,]

>x=df1 [, 2]; y=df1 [, 3]; lm.sol=lm(y～1+x)

>dwtest(lm.sol)

#对回归分析报告lm.sol中的回归模型作DW检验

结果显示,统计量DW值等于2.221,显著性概率为0.555,与自相关系数的显著性概率0.523相当,同样表明模型不存在自相关现象。

2.3 预测

对于例1的模型,如果已知火灾地点与消防站的距离x0=7km,那么相应的火灾损失y0可以用R来预测。

>df=read.csv(“file1.csv”); x=df [, 2]; y=df [, 3]; lm.sol=lm(y～1+x)

>x0=data.frame(x=7)

#新自变量的值应以1行1列的数据框形式输入

>y0=predict (lm.sol, x0, interval=“prediction”, leval=0.95); y0 #输出为点估计值与置信区间,参数interval缺

省,则不显示置信区间,leval用来指定置信度

结果显示,火灾损失的点估计值是44.713千元,95%的置信区间是(38.657,50.769)(千元)。

3 多元线性回归的R方法

下面举例介绍多元线性回归的R方法。

例2 影响一个地区居民消费的因素有很多,本例选取某地区食品花费x1、服装花费x2、职工平均工资x3、人均GDPx4、消费价格指数x5、失业率x6等9个解释变量,研究城镇居民家庭平均每人全年的消费性支出y。数据来源于2013年《中国统计年鉴》[2]65。数据文件为存储于工作目录的“file2.csv”。

3.1 偏回归系数及假设检验

>df=read.csv (“file2.csv”); x1=df[, 2]; x2=df [, 3]; x3=df [, 4]; x4=df [, 5]; x5=df [, 6]; x6=df [, 7]

>x7=df [, 8]; x8=df [, 9]; x9=df [, 10]; y=df [, 11]

>lm.sol=lm (y ～ 1+x1+x2+x3+x4+x5+x6+x7+x8+x9); summary (lm.sol)

系统输出与一元线性回归的输出基本类似。输出结果显示,变量x1,x2,x3,x5对y的影响具有显著性意义,而x4,x6,x7,x8,x9对y的影响不具有显著性。回归方程方差分析的显著性概率小于2.2×10-16,回归方程是:

具有统计意义,决定系数0.9923,修正的决定系数0.9889。总的来说这一模型并不理想,可能与自变量太多或自变量之间存在显著的相关性有关。下面采取逐步回归的方法改进模型。

3.2 逐步回归

>lm.step=step (lm.sol, direction=“both”);summary (lm.step)

#系统将输出逐步回归的中间步骤,下面只给出最终结果

Call:

lm(formula=y ～ x1+x2+x3+x5)

Residuals:

Residual standard error: 364 on 26 degrees of freedom

Multiple R-squared: 0.9916, Adjusted R-squared: 0.9903

F-statistic: 769.2 on 4 and 26 DF, p-value: <2.2e-16

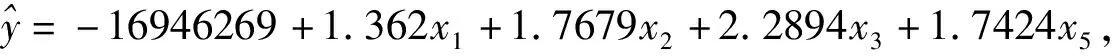
3.3 残差分析

3.3.1 异常点检测

>sre=rstandard (lm.step)

>srelogic=abs (sre)>qt (0.975, length (y)-4-1); srelogic

#按0.05双侧t界值判断,第17个样本点是异常点

>srelogic=abs (sre)>qt (0.995, length (y)-4-1); srelogic

#按0.01双侧t界值判断,没有异常点

3.3.2 异方差检验

>e=residuals (lm.step)

>y.fit=predict(lm.step)

#计算每一个样本点的因变量的估计值存储于向量y.fit

>cor.test (y.fit,abs (e), method=“spearman”)

#对因变量的估计值与残差e的绝对值作等级相关分析

多元线回归模型的异方差检验是通过检验因变量的拟合值y.fit与残差的绝对值abs(e)的等级相关性进行分析。结果显示,等级相关系数是0.25,显著性概率是0.174>0.05,所以该模型没有异方差现象。

3.3.3 自相关检验

检验多元回归模型是否存在自相关现象,同样需要在回归分析前对存储数据的数据框的行记录进行排序,一般按因变量升序排序。

>df=read.csv(“file2.csv”);dfo<-order(df[,“y”]);df1=df[dfo,]

>x1=df1[,2];x2=df1[,3];x3=df1[,4];x4=df1[,5];x5=df1[,6];x6=df1[,7];x7=df1[,8]

>x8=df1[,9];x9=df1[,10];y=df1[,11]

>lm.sol=lm(y～1+x1+x2+x3+x4+x5+x6+x7+x8+x9);lm.step=step(lm.sol,direction=“both”)

>e=residuals(lm.step);e1=e[1:30];e2=e[2:31]

>cor.test(e1, e2)

结果显示,相邻两点的残差的相关系数仅为0.169,显著性概率为0.371>0.05,说明该模型不存在自相关现象。

另一方面

>library (zoo); library (lmtest); dwtest (lm.step)

结果显示,统计量DW值等于1.611,显著性概率为0.106,同样表明模型不存在自相关现象。

3.4 预测

如果某地区居民的食品花费x1=5000元、衣着花费x2=1500元、居住花费x3=1000元、文教娱乐花费x5=1400元,那么可以预测该地区居民消费支出。

>x0=data.frame(x1=5000,x2=1500,x3=1000,x5=1400)

>y0=predict(lm.step,x0,interval=“prediction”,leval=0.95);y0

#输出为点估计值与置信区间,参数interval缺省

结果显示,该地区居民消费支出点估计值为12507.17元,95%的置信区间为(11709.78,13304.56)(元)。

4 结语

文章仅仅讨论符合基本假设情形下的回归分析过程。当违背基本假设时,诸如出现异常点、存在异方差现象或存在自相关现象时应该如何处理,以及回归分析的其它内容,因为篇幅关系,笔者将另文撰述。