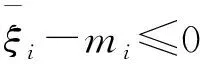具有变时滞的随机忆阻神经网络在固定时间内的控制同步
蒲 浩, 黄建文, 秦 进, 王正伟, 王 杏
(1. 遵义师范学院 数学学院, 贵州 遵义 563006; 2. 西南大学 数学与统计学院, 重庆 400715)
Chua等[1]根据电路变量的对称性与逻辑性,从理论上提出了忆阻器的概念,但是在之后的几年没有受到研究者的广泛关注,直到2008年惠普实验室制造出忆阻器后[2],由于其具有许多优良的特性,比如有非易失性、低功耗、多重记忆及纳米尺度等特点,使得忆阻器在非易失性存储器[3]、安全通信[4]、模拟电路[5]、图像处理[6]、密码学[7]等许多领域都有着广泛的应用前景. 为此,引起了研究者对忆阻神经网络的广泛研究[8-9].
近年来,尤其对忆阻神经网络的控制同步进行了广泛的研究,按照控制同步时间t,主要分为无限时间控制同步[10-11]和有限时间控制同步[12-13].
Wang等[11]通过李雅普诺夫函数法和随机微分包含理论研究了具有随机扰动和变时滞的忆阻神经网络的指数同步;Abdurahman等[13]基于恰当的外部输入控制器和有时间内的稳定性理论,研究了具有变时滞的忆阻神经网络在有限时间内的同步问题.然而,在实际应用和科研中,忆阻神经网络在当时间t→+∞时才实现控制同步,显然不符合高效的要求.为此,Ryan[14]提出了有限时间内的稳定性理论,但是,神经网络在有限时间内的控制同步中,有限时间T依赖于驱动-响应系统的初值,有限时间T是驱动-响应系统初值的函数; 此外在一些实际问题中驱动-响应系统的初值难以确定或者无法确定,导致有限时间T无法确定.为了解决此问题,在2012年Polyakov提出了独立于驱动-响应系统初值在有限时间内稳定的理论,即固定时间内稳定的理论[15].Chen等[16]、Zhen等[17]、Wei等[18]对忆阻神经网络在固定时间内的控制同步问题进行了研究.Chen等[16]通过固定时间稳定性理论研究了惯性忆阻神经网络在固定时间内的控制同步;Zhen等[17]研究了变时滞忆阻模糊神经网络在固定时间内的控制同步问题;Wei等[18]研究了变时滞惯性忆阻神经网络在有限时间和固定时间内的同步问题.然而,神经网络在控制同步的过程中受到噪声和时滞的影响,为此需要考虑随机扰动和时滞对神经网络控制同步的影响.但是,对具有随机扰动和混合变时滞的忆阻神经网络在固定时间内的控制同步的研究较少.
受此启发,本文通过构造一个恰当的外部输入控制器,基于固定时间稳定性理论,研究具有混合变时滞的随机忆阻神经网络在固定时间内的控制同步.
1 模型和预备知识
考虑如下具有混合变时滞的随机忆阻神经网络模型:
(1)

(2)
系统 (1)的初值条件为
xi(s)=φi(s)s∈[t0-τ,t0],t0≥0,i∈I
为了得到本文的结论,对于系统(1),假设
(H1) 对任意的xj,yj∈R,j∈I,存在正常数Mj>0,Lj>0使得
|fj(xj)|≤Mj
|fj(yj)-fj(xj)|≤Lj|yj-xj|
成立.
且
βij(t,0,0)=0
把系统 (1) 作为主驱动系统,引入如下的响应系统:
dyi(t)=[-di(yi(t))yi(t)+
Ii+ui(t)]dt+
i=1,2,…,n
(3)
式中
(4)
响应系统 (3) 的初值条件是yi(s)=φi(s),s∈[t0-τ,t0],i∈I,其中φ(s)=(φ1(s),φ2(s),…,φn(s))T∈C([t0-τ,t0],Rn).定义ei(t)=yi(t)-xi(t).
记
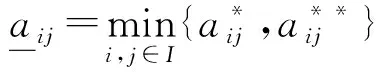
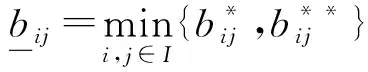

显然在驱动系统(1)和响应系统(3)中等式的右端是不连续的,为此本文在Filippove意义下研究其解在固定时间内的控制同步问题.由集值映射和随机微分包含理论,驱动系统(1)和响应系统(3)的解满足:
(5)
和
dyi(t)∈{-co[di(yi(t))]yi(t)+

i=1,2,…,n
(6)
式中
式(5)和式(6)也可以等价地表示为

i=1,2,…,n
(11)
和
(12)
式中
本文的主要目的是,通过构造一个恰当的外部控制输入控制器ui(t),使得驱动系统(1)和响应系统(3)在独立于其初值的有限时间内实现控制同步,其中外部输入控制器:
其中:0<λ<1,μ>1,ν>p>1,αi>0,ωi>0,ki>0.
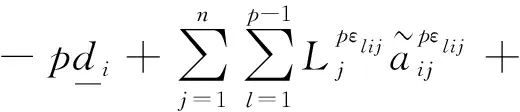

其中:εlij,ϑlij,γlij,σlij,ηlij是非负实数.满足:
根据式(11,12),可以得到如下的误差系统:

i=1,2,…,n
(13)
定义1若存在一个独立于驱动系统(1)和响应系统(3)的初值φ(s),φ(s),s∈[-τ,0]的有限时间T,使得
且当t≥T时‖y(t)-x(t)‖=0,则称驱动系统(1)和响应系统(3)的解x(t)和y(t)在固定时间T内同步.
2 辅助引理
为了证明结论的需要,引入下列引理:
引理1[18]如果h1,h2,…,hn是正实数且0<θ 引理2[19]设V(.):→R+∪{0}是一个连续径向无界函数,若满足条件: 1)V(x)=0⟺x=0; 2) 误差系统(13)的任意解e(t),当存在常数α>0,β>0,0<ν<1,q>1时使得 则V(t)=0,t≥T(x0),其中 引理3对于任意的i∈I,则 成立. 证明下面分4种情况对引理3进行证明: 情形Ⅰ:如果 |xi(t)|≤Ti且|yi(t)|≤Ti,则 情形Ⅱ:如果|yi(t)|>Ti且|xi(t)|>Ti,则 情形Ⅲ:如果 |xi(t)|≤Ti和 |yi(t)|>Ti,则 情形Ⅳ:如果 |xi(t)|>Ti且 |yi(t)|≤Ti,则有 综上4种情形: 成立. 定理1如果(H1),(H2) 成立,且ξi-ki≤0,则驱动系统(1)和响应系统(3)在恰当的外部控制输入ui(t)下,在固定T内是同步的. 证明构造如下形式的 Lyapunov 函数: 由伊藤公式,沿着误差系统(13)关于t计算V((e(t)))的Dini右上导数,可得到 (14) 根据假设(H1)及式(7~10)可知: (15) (16) (17) 成立. 结合式(15~17),由假设(H2)和引理3,式(14)变为 πi|ej(t-ρ(t))|p+(αi|ei(t)|λ+ ωi|ei(t)|ν)))+p(ei(t))p-1sign(ei(t))× (18) 结合式(18~22)可得到 (23) 由引理1可知: (24) (25) 结合式(24,25),对式(23)两边取数学期望,可知: (26) 式中:α=mini∈I{αi};ω=mini∈I{ωi}. 注1Ding等[20]研究了一类多种变时滞的随机忆阻神经网络当时间t→+∞时实现同步的问题;Zhang等[21]通过分布脉冲控制的方法研究了随机时滞的忆阻神经网络的指数同步问题.而本文研究的是随机忆阻神经网络在有限的时间内实现控制同步,且有限时间T独立于系统的初值,即本文理论更符合实际应用的需要. 注2由定理1的条件ξi-ki≤0可知,混合变时滞和随机扰动对忆阻神经网络在固定时间内的控制同步有抑制作用. 当p=2时,构造如下的与转换跳跃Ti无关的外部输入反馈控制器 推论1如果(H1),(H2)成立,在外部输入Si(t)控制下,则驱动系统(1)和响应系统(3)在固定时间T内是同步的. 证明过程和定理1的类似,不再重复. 注3Han等[22]研究了具有混合变时滞的忆阻神经网络的自适应同步,文中所得的同步结论中没有和转换跳跃Ti建立关系,故本文结论更加符合实际问题及应用.Abdurahman等[13],Ryan[14]研究了忆阻神经网络在有限时间内的控制同步问题,没有考虑噪声强度对系统控制同步的影响.本文中当噪声强度βij(t,0,0)=0时且ui(t)中ωi=0时,构造如下的外部输入控制器: 其中:0<λ<1,mi>0, 注4推论1中的有限时间T是依赖于驱动系统(1)和响应系统(3)的初值条件的函数,当初值不同时,控制同步的有限时间会不同.而本文研究的是控制同步时间独立于驱动系统(1)和响应系统(3)的初值. 致谢:本文得到遵义师范学院2017年学术新苗培养及创新探索培育项目(黔科合平台人[2017年]5727-24号)的资助,在此表示感谢.
3 主要结果


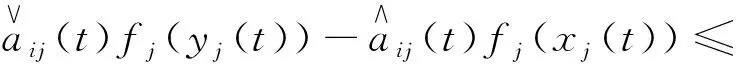
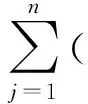

4 推论