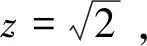基于电-力导纳型类比法电厂动力设备被动隔振机理分析

兰江，傅永平，杨光弟

(滇西科技师范学院 数理学院，云南 临沧 677000)

电厂拥有各种大中小型动力设备，其中以锅炉[1]、汽轮机等大型动力机械为主，其辅助设备包括磨煤机、碎煤机、送风机、鼓风机，给水泵等。各种动力设备同时运行时，设备之间振动将通过地基传递相互干扰，使设备质量中心和力中心发生偏移，造成某些设备不能平稳运行，严重时将造成设备损坏和经济损失[2]，因此，为保障动力设备的安全运行，有必要对其采取隔振处理。

当前，采用弹簧作为缓振介质作用于动力设备的基础端，可提高机械设备的使用寿命[3]，减少来自基础端振动对动力设备及环境的影响[4-10]，能有效提高设备的使用寿命、延长大修周期，提高经济效益。目前，国内外学者研究偏向于对弹簧本身的动力学性能、隔振机制[11-14]以及现场测试分析与改造[15-16]方面的研究，对动力设备隔振技术理论分析的较少。因此，本文基于电-力导纳型类比法，对单自由度弹簧被动隔振技术的隔振机理进行分析，其分析结果对于电厂动力设备的隔振设计及安全运行评估具有一定的借鉴意义。

1 电-力导纳型类比设备阻尼振动模型

如图1所示，Mm表示需要进行隔振的动力设备，而外界干扰自基础传来。设定质量Mm的平衡位置为坐标原点O，设备的位移为A，速度为v。弹簧置于阻尼物质中，其弹性系数为Km，力阻为Rm。弹簧与基础相连的一端坐标记为O1，外界扰动通过基础传递到弹簧上。基础端受到周期性扰动后产生的位移振幅为A0，则扰动圆频率为ω的设备位移A1可表达为

A1=A0eiωt

(1)

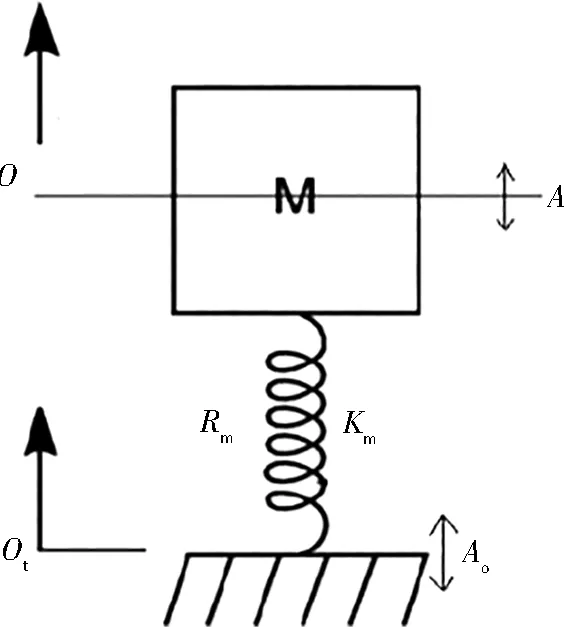
图1 简谐振动系统

其对应的电-力导纳型类比线路[17]如图2所示。

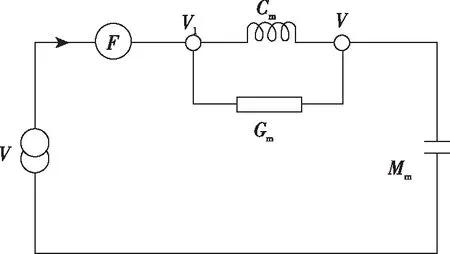
图2 电-力导纳型类比电路

从物理角度分析知，弹簧与力阻元件的速度应保持一致，设v1，而质量元件受v控制。因此，弹簧两端的速度差应为v1-v，这在图2中也得到了反映。由图2，应用克希霍夫电路定律有

(2)

式中：Gm=1/Rm，为力导；

Cm=1/Km，为力顺。

由式(1)、式(2)整理得：

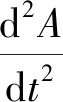
(3)

将式(1)分别代入式(3)，得：

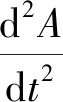
(4)

式(4)为二阶非齐次常微分方程，其一般解为

A=A0e-δtcos(ω0t-φ0)+Aaej(ωt-θ0-π/2+θ)

(5)

式(5)右边第一项为瞬态解，它描述系统自由衰减振动状态；第二项为稳态解，即系统在外力扰动下，被迫进行强制性振动的状态，而在一般设备运行中产生的扰动是具有周期性和规律性的稳定扰动，其振幅恒定，因此，本文仅研究基础在稳定扰动状态下对设备的干扰作用。

由式(5)知，在稳定扰动作用下，Mm的振动位移为

A=Aacos(ωt-θ0-π/2+θ)

(6)

将式(6)代入式(4)中，得稳态振动系统的振幅为

(7)

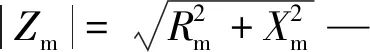
为描述动力设备在外界干扰作用下的响应特性，现定义如下变量：

(8)

式中：z—外界干扰频率与动力设备固有频率之比，称为频率比；

Qm—力学品质因子；

ω0—动力设备固有频率。

利用式(8)对式(7)进行归一化处理，得到归一化的位移响应特性公式，即

(9)

2 动力设备位移-速度-加速度响应特性分析

2.1 动力设备位移响应特性分析

根据式(9)，可得出动力设备的位移响应特性曲线，如图3所示。

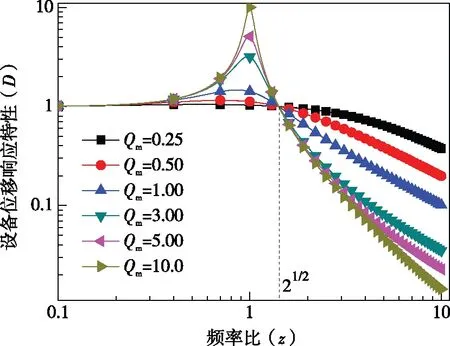
图3 设备位移响应特性曲线

(10)

从式(10)可以看出，系统的位移共振频率与固有频率并不相等，仅当Qm很大时，两者才接近相等。

将式(10)代入式(9)中，得到发生共振时设备的位移响应特性Dr。

(11)

当Qm=1时，Dr=6.646，这表明设备位移共振峰比平坦区的极限值高5.646倍。控制Qm越小，位移共振曲线越均匀，即系统越难发生共振。

基础的干扰不仅会使设备发生位移响应，还会连带发生速度和加速度响应。因此，有必要对设备的速度、加速度响应特性进行分析。

2.2 动力设备速度响应特性分析

将式(6)对时间取一阶导数，可得设备振动速度表达式：

υ=-ωAasin(ωt-θ0-π/2+θ)

(12)

则，其振幅为

υa=ωAa

(13)

结合式(9)，对式(13)归一化处理，得到设备速度响应特性公式：

(14)

图4按式(14)给出了设备速度响应特性曲线。

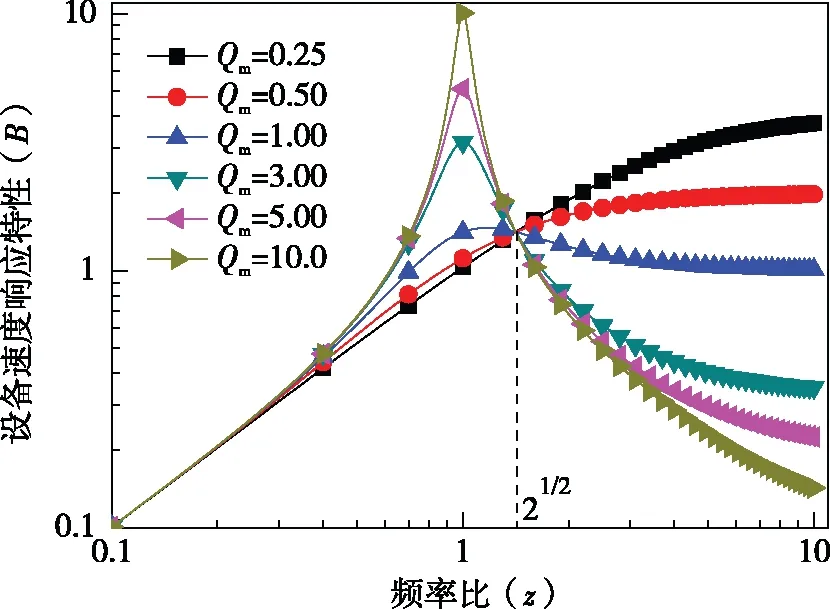
图4 设备速度响应特性曲线

2.3 动力设备加速度响应特性分析

将式(6)对时间取二阶导数，可得设备振动速度表达式：

a=ω2Aacos(ωt-θ0-π/2+θ)

(15)

则其振幅为

aa=ω2Aa

(16)

结合式(9)，对式(16)归一化处理，得到设备加速度响应特性公式：

(17)

图5按式(17)给出了设备加速度响应特性曲线。

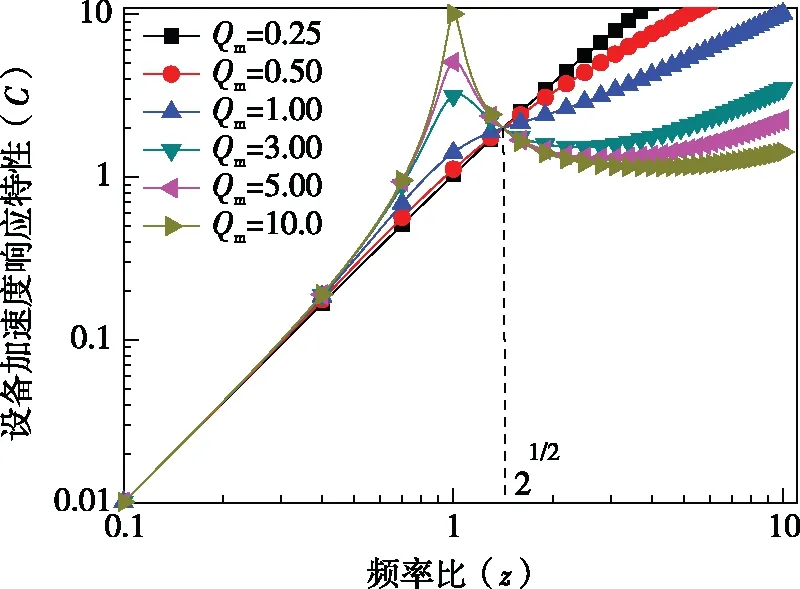
图5 设备加速度响应特性曲线

2.4 动力设备位移-速度-加速度振幅定性分析

对于公式(9)、(14)、(17)，当z≫1时，即基础的干扰频率远大于系统固有频率时，设备位移-速度-加速度振幅分别近似为Aa≈Fa/(ω2Mm)，υa≈Fa/(ωMm)，aa≈Fa/Mm a；由此分析知，设备质量对振动起到主要作用，质量越大，系统响应越小，且加速度振幅与频率无关，而位移和速度分别与频率二次方、一次方成反比。当z≪1时，公式(9)、(14)、(17)振幅分别近似为Aa≈Fa/Km，υa≈Faω/Km，aa≈Faω2/Km；这时弹簧的弹性系数对振动起到主要作用，弹性系数越大，振幅越小，且位移振幅与频率无关，而速度和加速度振幅分别与频率一次方、二次方成正比；而当z>|z2-1|Qm时，公式(9)、(14)、(17)振幅分别近似为Aa≈Fa/(ωRm)，υa≈Fa/Rm，aa≈Faω/Rm，这时系统的力阻对振动起到主要作用，力阻越大，振幅越小，且速度振幅与频率无关，而位移振幅和加速度分别与频率一次方成反比和正比。

以上通过对设备位移响应特性、速度响应特性和加速度响应特性的分析发现，力学品质因子Qm对系统的响应特性具有十分重要的影响作用，为此，在对设备进行隔振处理时，应根据系统的实际情况选取具有合适力阻和弹性系数的弹簧。

3 力学品质因素Qm对设备响应特性的影响

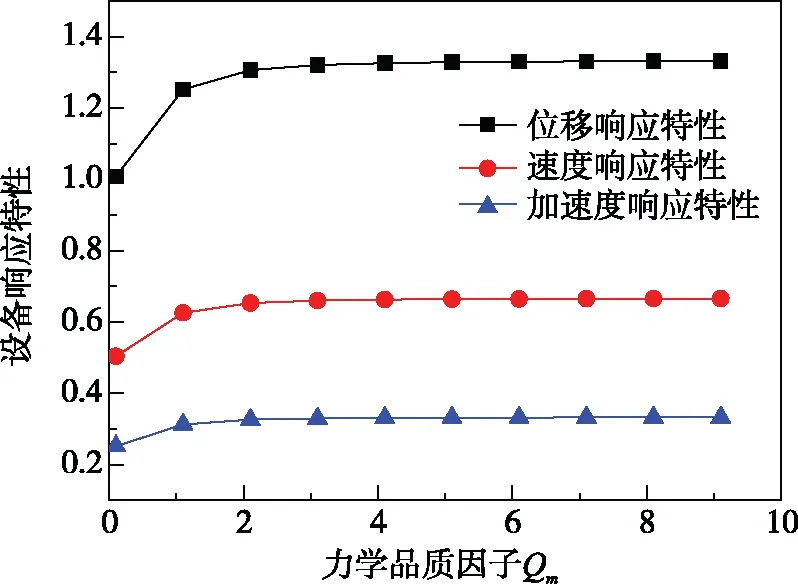
图6 频率比z=0.5时，Qm对设备响应特性的影响

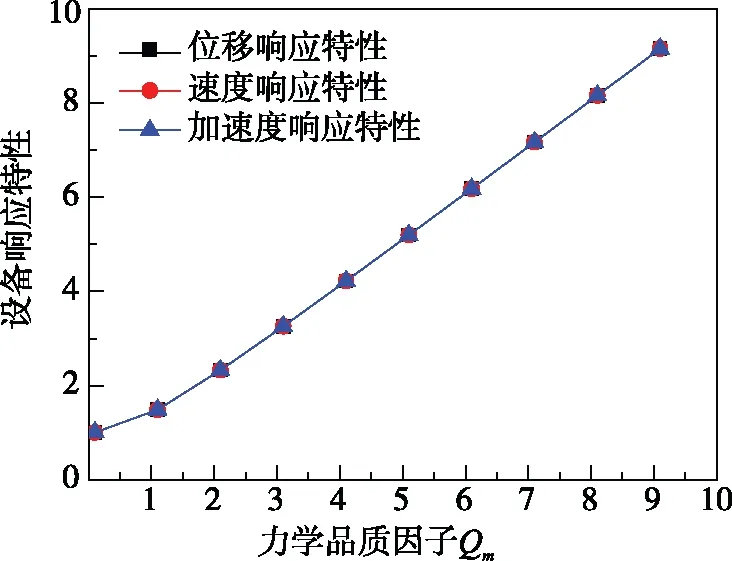
图7 频率比z=1.0时，Qm对设备响应特性的影响

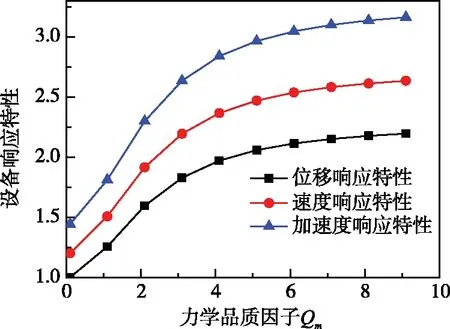
图8 频率比z=1.2时，Qm对设备响应特性的影响

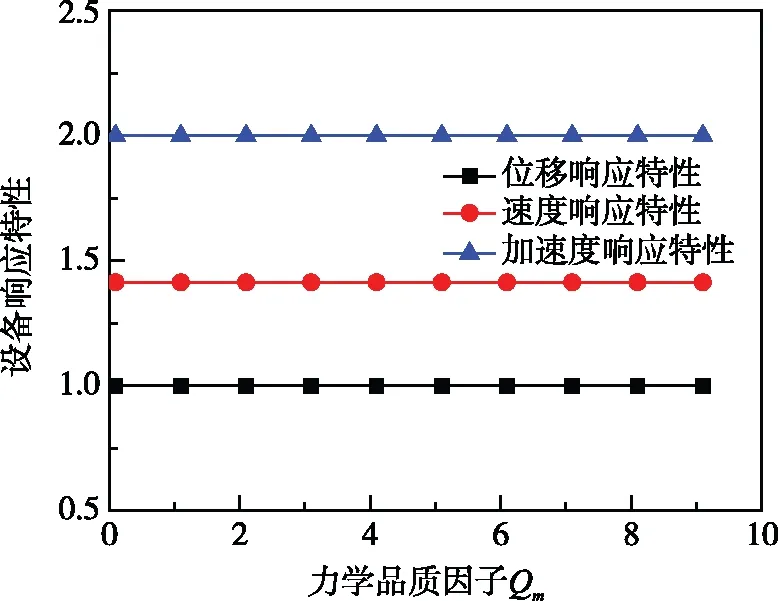
图9 频率比时，Qm对设备响应特性的影响

图10 频率比z=10时，Qm对设备响应特性的影响

由图6分析知，当z=0.5时，D、B、C随Qm增加而缓慢增加，且当Qm>2以后基本趋于平稳。且分析知，在z<1时，来自基础的干扰经过弹簧传递给设备的扰动对B、C较小，而对D影响较大。其响应特性关系为D>B>C。

由图7分析可知：当z=1时，即基础干扰频率等于系统固有频率时，设备位移、速度和加速度响应特性曲线基本重合。这表明在该条件下，受基础的干扰使设备的位移响应、速度响应和加速度响应同时发生；且随Qm增大，响应越剧烈，因此，为保证系统平稳运行应避免该情况发生，其响应特性关系为D=B=C。

由图8可知：当z=1.2时，D、B、C随Qm增加迅速增大(Qm<2)，而后缓慢增大并逐渐趋于平稳，其响应特性关系为C>B>D。

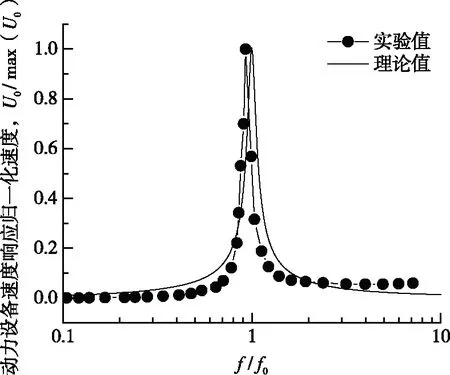
由图10可知：当z=10时，D、B、C随Qm增加迅速减小(Qm<2)，而后缓慢降低并最终趋于平稳，其响应特性关系为D

综合以上分析发现：在z<1时，设备响应特性关系为D>B>C；而在z>1时，设备响应特性关系为D

4 与实验数据对比

为验证理论推导得到的动力设备响应特性公式的可靠性，图11将动力设备速度响应特性与文献[11]中的实验数据进行了对比。文献[11]给出了滑油泵模型安装广义质量弹簧减振器后，机座与隔振器连接点振动加速度频率响应特性实验曲线。本论文的研究对象是对具有单自由度的动力设备进行隔振机理分析得到的相关理论结果；同时，文献[11]中也是以单自由度的动力模型进行实验的，因此，应当可以将其获得的实验数据用于验证本文的理论结果。系统固有频率为f0=15 Hz。将实验中的加速度频率响应分贝值，按照公式(18)折算为振动速度值。

(18)

式中：Uref—参考速度，Uref=4.83×10-8m/s；

SPL—声压级，dB。

为便于对比，对纵坐标数据进行归一化处理后进行对比，如图11所示。

图11 理论值和实验值对比

由图11知，理论值与实验值吻合度较高，这佐证了本文推导得到的动力设备响应特性公式的可靠性，因此，方程(9)、(14)和(17)可用于对单自由度隔振系统的动力学特性分析。

5 结 论

本文讨论了不同频率比(z)和力学品质因素(Qm)对设备位移(D)、速度(B)和加速度(C)响应特性的影响，并进行了定量分析。经与实验数据对比分析，验证了动力设备响应特性公式(9)、(14)、(17)的可靠性，其可作为对电厂动力设备进行隔振设计及安全运行评估的依据。此外，本文的理论结果可用于具有单自由度振动特征的动力设备隔振分析。并得到如下结论：

(2)在z<1时，设备响应特性关系为D>B>C,且随着Qm增加D、B、C逐渐趋于平稳，分别为1.33，0.67，0.33；而在z>1时，设备响应特性关系为D