基于LSTM循环神经网络的停车需求预测研究

□ 靳 猷

(北京公联交通枢纽建设管理有限公司，北京 100000)

目前，国内外关于停车需求预测的研究较多。大致可分为统计分析与机器学习[4]。张雷通过引入时间序列模型，基于停车场的车辆出入数据，对其进行了实时预测[5]，Cheng等人针对典型停车到达和离开规律分布，利用马尔科夫生死过程建立停车需求预测模型[4]。随着机器学习领域的发展，一些神经网络模型也被应用到了需求预测中，并获得了较好的应用。高健夫等人利用BP神经网络进行泊位预测，得到较好的停车需求预测模型[6]。但由于BP神经网络模型本身存在全局性差，易陷入局部最优等缺陷，而为避免出现梯度消失的问题，1997 年Hochreiter和Schmidhuber提出了长短期记忆网络(Long-term and Short-term Memory Network,LSTM)[7]，解决了一般的 RNN 存在的长期依赖问题，裘瑞清利用BP神经网络和LSTM循环神经网络实现泊位需求的短时预测，结果表明LSTM循环神经网络的预测效果明显优于BP神经网络[8]。LSTM循环神经网络目前已被广泛应用于社会各个领域，如电力行业、物流库存量等。徐尧强等人用电量和温度、风速、相对湿度、降水之间的动力学因果关系为研究对象，建立长短时记忆网络模型，并将建立的模型应用在市用电量预测中，验证了 LSTM 神经网络模型在城市用电量预测中的实用性[9]；王渊明以电商行业的历史销售数据为研究对象，构建LSTM 神经网络模型对其进行预测，并对照了BP神经网络预测结果，发现LSTM的误差结果明显低于BP神经网络[10]。但基于神经网络需要大量的停车标签数据的现实情况，目前普遍缺乏公开的停车数据，导致LSTM 神经网络仍未被广泛应用于停车需求预测研究中。

本文主要针对停车场的停车需求问题，利用LSTM循环神经网络算法进行预测，首先对算法进行简要介绍和分析，构建泊位需求预测模型，以北京市宋家庄停车场为实验对象进行停车需求预测。

1 LSTM循环神经网络介绍

基础的神经网络包括输入层、隐含层和输出层，通过激活函数控制输出，层与层之间通过权值连，步骤如下。

步骤1：网络初始化。根据系统给定的序列(x,y)确定网络输入层节点数I、隐藏层节点数J，输出层节点数K，初始化输入层、隐含层和输出层之间的链接权重wij和wjk，初始化隐含层偏置a和输出层偏置b，给定学习率和激活函数。

步骤2：计算隐含层输出。

(1)

其中，f为激活函数，如sigmoid，如式(2)所示。

(2)

步骤3：计算输出层，如式(3)所示。

其中，hj表示各消费支出项目与产业结构的和谐度，wj表示各消费项目所占权重，通常用各项消费支出在总消费支出中所占比重来表示。

(3)

步骤4：误差计算，如式(4)所示。

ek=Ok-Yk,k=1,2,…,K#

(4)

步骤5：利用梯度下降法更新权值和偏置，以减小误差。

RNN与一般神经网络的区别在于其存在神经元反馈连接，这种形式的连接使得网络能够以一种激励的形式存储最近时间段的输入数据信息(短时记忆)，即循环神经网络在t时刻的输入完成与输出的映射且参考了t之前所有输入数据对网络的影响，形成了反馈网络结构。但RNN在训练过程中可能发生的梯度消失现象，致使RNN只能短期记忆，由此LSTM网络被提出。LSTM与RNN的区别在于细胞的结构和运算，LSTM中细胞由输入门、遗忘门和输出门组成，其核心概念在于细胞状态与“门”结构。遗忘门决定了上一时刻(t-1)的单元状态ct-1对当前时刻(t)ct的影响程度，计算公式如式(5)所示。

fc=σ(Wf·[ht-1,xt]+bf)#

(5)

其中，ft为遗忘门状态结算结果，Wf为遗忘门的权重矩阵，bf为遗忘门的偏置，σ为激活函数。

输入门决定当前时刻网络的输入xt对单元状态ct的影响程度，计算公式如式(6)。其中，bi为遗忘门的偏置，it为输入门状态结算结果，Wi为输入门的权重矩阵。

it=σ(Wi·[ht-1,xt]+bi)#

(6)

当前时刻输入的单元状态根据前一时刻的输出和当前时刻的输入确定，计算公式如式(7)。

(7)

输出门控制单元状态ct对当前输出值ht的影响程度，计算公式如(8)所示。

ot=σ(Wo·[ht-1,xt]+bo)#

(8)

其中,ot为输出门状态结算结果，ht=ot·tanh(ct)，Wo为输出门的权重矩阵。

由此完成LSTM的正向传播过程。

2 停车需求预测的 LSTM 模型构建

数据预处理。

本文使用的数据来源于北京公联枢纽建设管理有限公司负责管理运营的宋家庄枢纽停车场2019年10月1日至2019年12月31日共92天的车辆出入记录，通过对数据进行预处理，获得了宋家庄枢纽停车场2019年10月1日至2019年12月31日共92天时间间隔为1小时的泊位需求值，具体的泊位需求变化如图1所示。

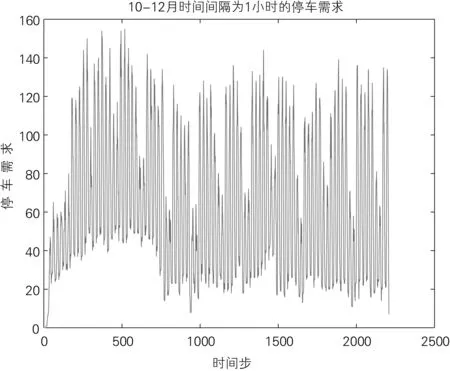
图1 10-12月时间间隔为1小时的停车需求

如图1所示，工作日和双休日的停车需求数量基本趋于稳定，且具有一定规律，工作日停车需求普遍高于双休日，其中10月1号至10月7号为法定节假日，故停车需求数量较少，符合实际情况。

3 结果分析

3.1 模型构建和参数设置

本文的预测过程使用所有数据中前90%共82天的数据作为训练集，后10%用于测试。LSTM回归网络由1个输入层、1个隐藏层(200个隐含单元)、1个输出层组成。在网络训练中，采用“adam”算法加速网络收敛[11]，并进行 250 轮训练。其中，网络中的状态激活函数选取的是双曲正切函数(tanh)，门激活函数选取的是simoid，损失函数选取均方误差(RMSE)。同时，为防止梯度爆炸，将梯度阈值设置为 1，并指定初始学习率 0.005，在 125 轮训练后通过乘以因子 0.2 来降低学习率。

3.2 误差结果分析

预测过程中，将响应指定为将值移位了一个时间步的训练序列。也就是说，在输入序列的每个时间步后，LSTM 网络都学习预测下一个时间步的值。初始化网络状态后，对训练数据进行预测。接下来，使用训练响应的最后一个时间步进行第一次预测，即完成预测过程。

训练过程如图2所示，随着迭代次数的增加，均方误差(RMSE)和损失逐渐减小并收敛，当迭代次数达到50，RMSE和损失趋于平稳。

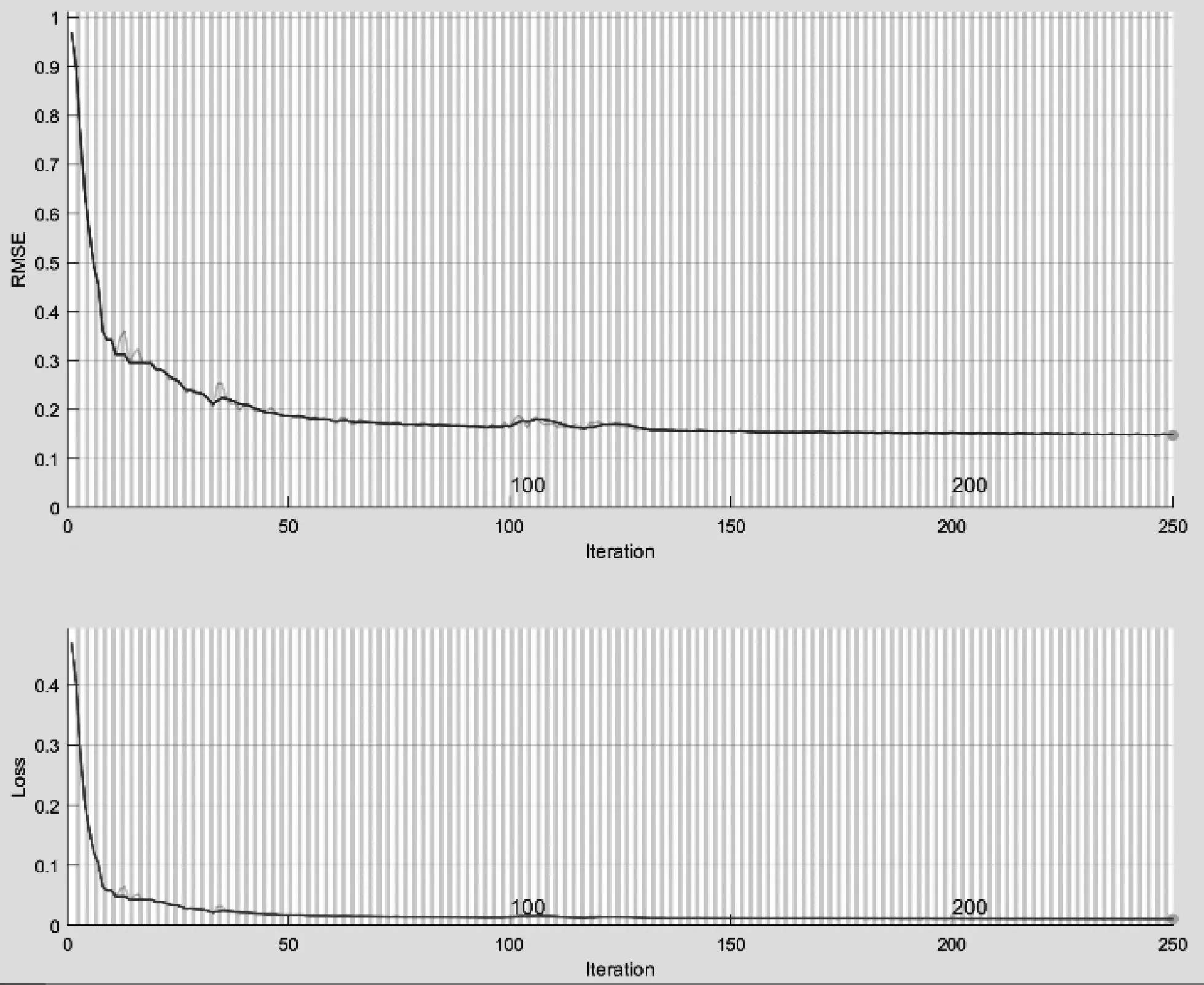
图2 LSTM循环神经网络训练过程

预测结果如图3所示，利用LSTM神经网络训练得到的模型对10月-12月92天后10%的数据进行预测，通过对比停车需求预测值和观测值，发现均方误差RMSE为22.605，误差较小，但是如图4所示，预测值与观测值存在一定误差，且未体现工作日和双休日的停车需求数量变化特征。

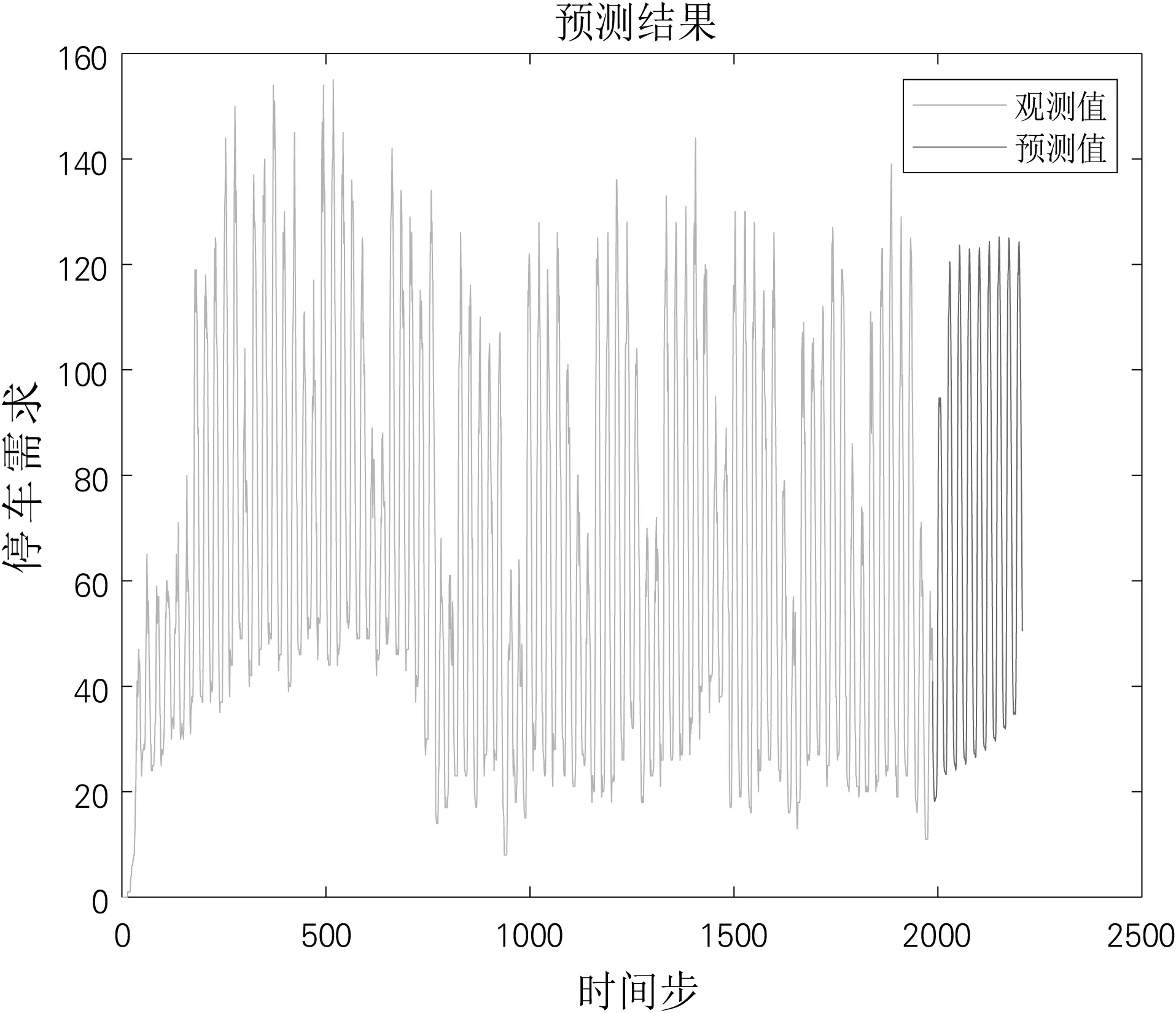
图3 LSTM神经网络预测结果图

图4 观测值与预测值对比图

为对预测结果进行更细致的分析，从全部数据中的后10%中随机提取工作日一天，周末一天进行神经网络模型测试，得到的结果如下。

对比图5和图6，任意工作日的预测结果明显优于任意周末的预测结果(RMSE=18.4763<32.9507)，这是由于普通工作日泊位需求变化较为稳定，且工作日数量较多，训练样本大，因此，得到的预测结果误差较小。

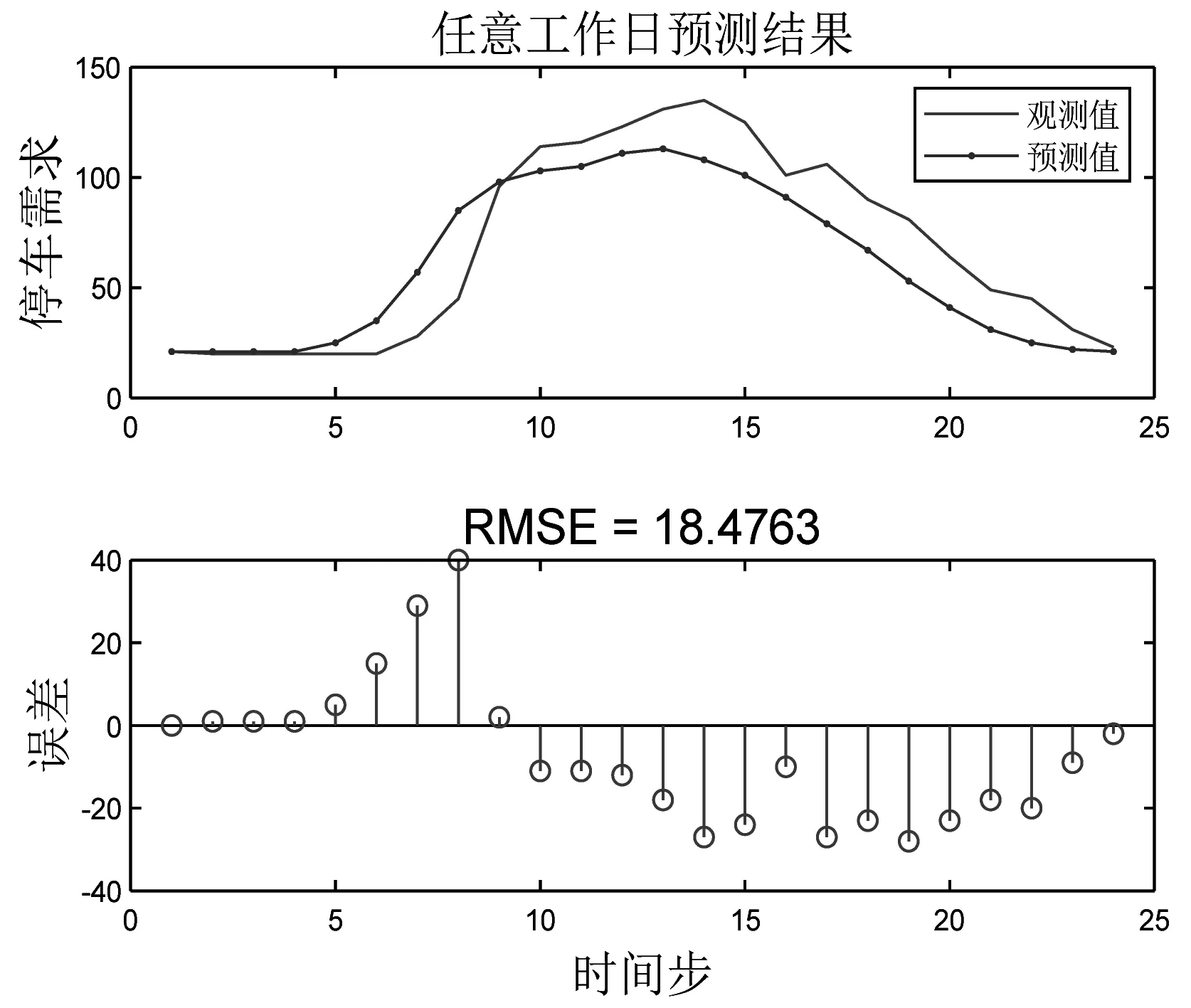
图5 任意工作日预测结果图

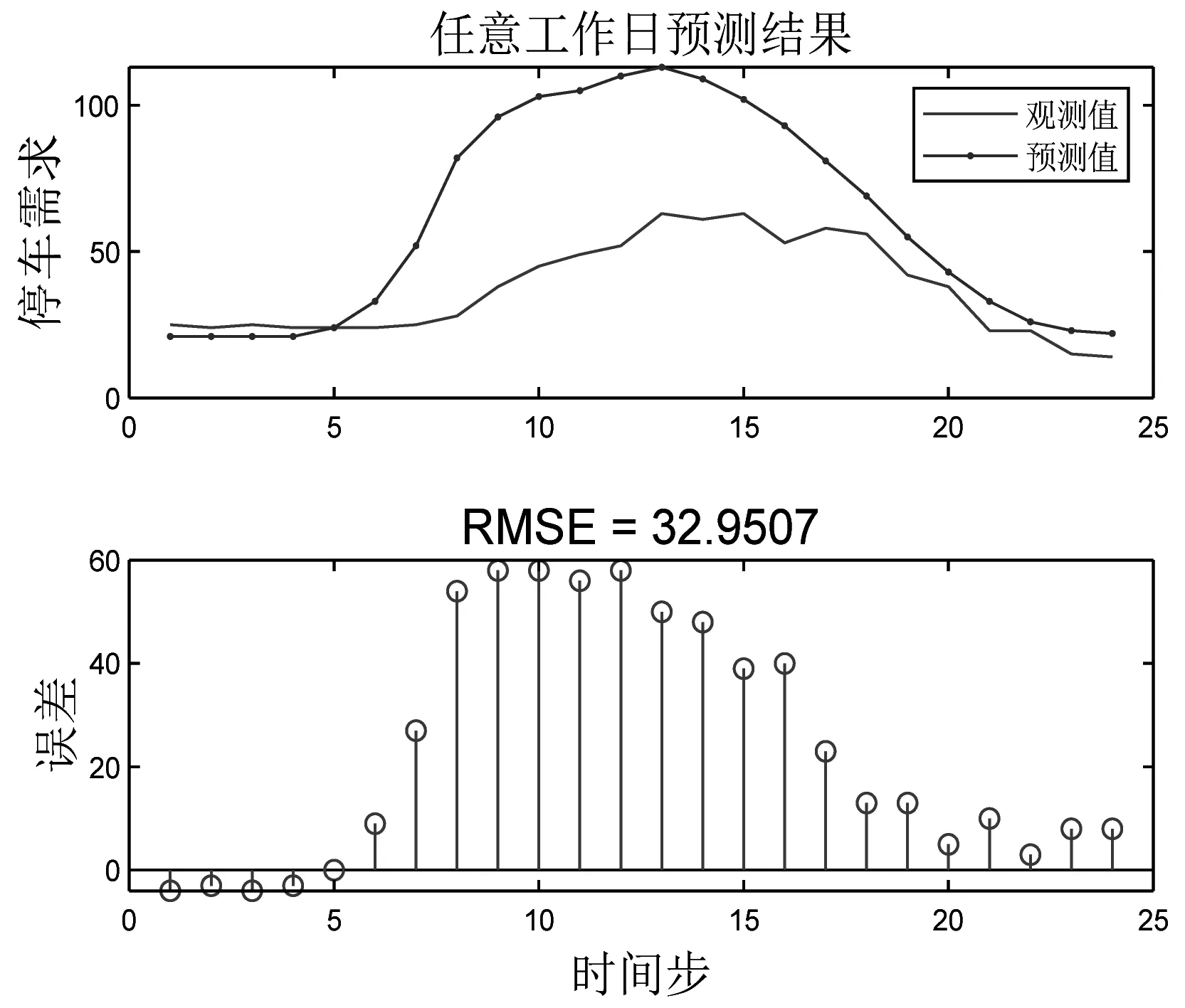
图6 任意周末预测结果

前文中，LSTM神经网络预测过程所使用的是停车需求预测值，若可以获取预测之前的时间步的实际值，则可以使用观测值而不是预测值更新网络状态，因此，为进一步分析LSTM神经网络预测结果，本文对两种预测结果进行了对比，如图4、7所示。

通过对比可知，使用观测值更新网络状态的误差明显低于使用预测值更新网络的结果(均方误差RMSE=5.8534远远小于22,605)，预测更加准确，且体现出了工作日和双休日的停车需求数量变化特征，说明相比于使用预测值更新状态的预测结果，使用观测值更新网络进行预测具有一定的优越性。

4 结论

停车需求预测对于缓解停车矛盾具有重要意义，当面对突发交通状况时可以帮助停车管理者更好地管理车位和道路交通。本文基于LSTM 循环神经网络，以公联枢纽宋家庄停车场3个月的车辆出入数据为研究对象，其中停车需求数据以小时为单位时间间隔，建立了停车需求预测模型，测试数据与实际数据的对比表明预测结果较为精确，能够较好地反映该停车场的车位使用情况与停车需求特性。

但该预测方法仍存在一定缺点，实验训练数据不足会导致某些特殊情况的预测情况并不十分理想(如周末)，此外，由于神经网络本身缺少理论支持，参数需要由经验决定，需要进行较长时间训练才能得到理想模型。