基于混沌游戏表示和自适应仿射传播聚类的股票板块分类
张紫璇 段红梅


【摘要】为对我国A股进行板块分类, 首先用混沌游戏表示算法对股票日收益率数据进行降维, 再用自适应仿射传播聚类算法得到将所有股票分为5类和11类两种板块的分类结果。 与证监会行业分类中类内外平均相关系数差0.0140相比, 分5类时类内外相关系数差均值为0.0284, 分11类时, 类内外相关系数差均值为0.0270, 均比证监会行业分类区分度高。
【关键词】混沌游戏表示;自适应仿射传播聚类;股票板块分类;A股
【中图分类号】F832.5 【文献标识码】A 【文章编号】1004-0994(2020)19-0152-4
一、引言
股票板块分类方法中应用最广的是按股票行业分类。 早在1966年, 美国学者Kahle等[1] 就指出股票价格的变动会受到行业分类的影响。 之后又有学者得出了行业因素能解释股票收益率26%波动率的结论[2] 。 现有的行业分类标准主要有ISIC行业分类、GICS、证监会行业分类、WIND行业分类、申银万国行业分类及中信证券行业分类等。 上市公司行业信息是上市公司对外应披露信息的重要方面。 上市公司行业分类方法的科学与否, 对于规范和提高上市公司信息披露质量、市场参与者对公司股票进行定价、投资者进行投资决策都有着直接的影响。 由于各种原因, 我国证券市场在建立之初没有对上市公司进行统一的分类, 上海、深圳证券交易所根据各自工作的需要, 分别对上市公司进行了简单划分:上交所将上市公司分为工业、商业、公用事业和综合四类; 深交所则分为工业、商业、公用事业、金融和综合五类。 近年来, 随着证券市场的发展、上市公司数量的激增, 两交易所原有分类的不足表现得越来越明显:分类过粗, 给市场各方对上市公司进行分析带来了很多不便。
本文采用混沌映射聚类算法, 根据上市公司的股票价格建立相关映射, 并且将该金融时间序列的相关系数与映射之间的耦合强度联系在一起进行分析。 以我国A股日收益率数据为数据源, 通过混沌游戏表示算法降维和自适应仿射传播聚类算法进行聚类分析, 从而获得新的上市公司板块分类结果, 对比原有的证监会行业分类结果, 本文提出的分类结果区分度更高, 类内外平均相关系数差别也更加明显, 与当前A股企业实际较为贴合。
二、模型构建
1. 数据。 根据上市公司的股票价格建立相关映射, 并且将该金融时间序列的相关系数与映射之间的耦合强度联系在一起进行分析, 基于本论文的分析诉求, 在对分析数据进行选择时, 以我国A股(包括上交所和深交所)2843只股票2007年1月1日 ~ 2017年1月23日的交易数据为对象, 将其日收益率作为聚类数据进行研究。
初始数据集一共包含3325只股票数据。 股市中通常把上市时间不足半年的股票称为新股, 而新股存在新股弱势且数据量少, 故删除268只发行时间少于180天的股票; 研究过程中, 发现有上百只股票自2016年5月1日起不再有交易数据, 数据缺失时间较长, 故删除2016年5月之后没有交易数据的116只股票; 删除B股。 剩余2843只股票。 在数据分析中, 本文充分考虑了2008年全球金融危机的影响和2015年A股股灾异常波动的影响, 对相关数据进行了相应处理, 以求在数据层面更加切实地反映正常交易市场下股票的数据信息。
证监会上市公司行业分类结果来自2017年2月16日在证监会网站发布的2016年四季度上市公司行业分类结果。 研究发现, 采用混沌游戏模拟可以实现数据的自然分割, 相同行业背景下的公司通常是聚合在一起的, 下文重点结合混沌游戏与上市公司交易数据进行整合分析。
2. 混沌游戏表示。 混沌游戏表示算法流程如下:①作一个正方形, 四个角分别表示DNA序列中的A、C、G、T四种碱基。 ②在正方形面上随机取一个初始点。 ③对于任意一个长度为N的DNA序列, 按照DNA序列中的碱基顺序, 用以下方法绘制混沌游戏表示(CGR)图:按顺序读取DNA序列的碱基, 绘制读到的碱基对应的角与初始点的中点, 并将这个中点设为新的初始点, 得到一张包含N+1个点的CGR图。 更具体地说, 令A、C、G、T分别为P1(0,0)、P2(4,0)、P3(4,4)、P4(0,4), CGRi(x,y)为要在CGR图中绘制的第i个点, Pi(x,y)是序列的第i个点, 按以下迭代公式得到CGR图中所有的点:CGRi(x)=[CGRi-1(x)+Pi(x)]/2,i=1,…,N; CGRi(y)=[CGRi-1(y)+Pi(y)]/2,i=1,…,N。
CGR图有以下性质:①当将CGR图用x=0,1,2和y=0,1,2分为如图1所示的4个分块时, 若CGRi(x)落在第一个分块, 按以上第一个迭代公式得到这个CGR点对应的DNA碱基一定是A, 其他三个分块类似。 ②参照第一条性质, 当将CGR图用x=0,1,2,3和y=0,1,2,3分割成16个分块时, 以AT块为例, 若CGRi(x,y)落在AT塊, 按以上第一个迭代公式得到这个CGR点对应的DNA碱基一定是A, 上一个DNA碱基为T, 其他分块类似。 ③当将CGR正方形进行更高维的剖分时, 类似的结论仍然成立。 基于CGR图的这个性质, 可以认为在CGR图中, 序列的顺序被充分表达。 将图2中的16个分块按1 ~ 16进行编号, 令Sk(k=1,2,…,16)为落在第k个分块内的CGR点数, 则Fk=Sk/N(k=1,2,…,16)。 其中N为DNA序列的长度, 这样任意一个序列都将能转化为一个16维的向量。
3. 混沌映射聚类算法。 在混沌映射聚类算法被引入作为主要算法时, 是将要被聚类的那些元素嵌入一个D维的特征空间里。 在这个框架下, 每个数据点都被看成在承载混沌映射动力学的网格上有一个对应的位置。 相应在原始数据空间中的高密度区域, 在静态的体系下同步映射聚类会出现。
4. 自适应仿射传播聚类算法。 仿射传播聚类在算法进行之前不需要确定最终聚类族的个数, 且适合大类数的聚类。 在算法开始时, 所有的数据点都被看作潜在的聚类中心。 在算法进行中, 仿射传播聚类算法为数据集收集信息得到两个重要的证据矩阵:吸引信息矩阵R和归属信息矩阵A。 r(i,k)描述了数据点k适合作为数据点i的聚类中心的程度; a(i,k)描述了数据点i选择数据点k作为其聚类中心的程度。 r(i,k)和a(i,k)越大, 证据越强, 数据点k作为最终聚类中心的可能性就越大。 仿射传播聚类算法在信息传递过程中, 两个矩阵的迭代过程如下:rt+1(i,k)=s(i,k)-max{at(i,k')+s(i,k')}, k'≠k; at+1(i,k)=min{0,rt(k,k)}+ max{0,rt(i',k)}, i≠i,k。 迭代完成后得到m个可行度较高的聚类中心和对应的聚类结果。
自适应仿射传播聚类算法输入变量数据集为待聚类变量集, 主要输出参数有以下几个:①矩阵“labels”, 以类标的形式存储不同类数的聚类结果; ②向量“NCs”,存放“labels”对应的类数;③“NCopt”, 存放最优类数, 最优类数对应的聚类结果可在“labels”中查找; ④“Sil”, 存放不同类数的聚类结果的Silhouette指标的平均值; ⑤“Silmin”, 存放每一个聚类结果中任意两个聚类Silhouette指标中的最小值。 Silhouette指标记为Sil(t):Sil(t)=[b(t)-a(t)]/max{a(t),b(t)}。 其中, a(t)为样本t和与它同一类内的其他样本的平均距离, b(t)表示样本t和其他类距离的平均值。 自适应仿射传播聚类中, 用Silhouette指标的平均值来反映聚类结果的优劣程度, 值越大表示聚类结果越好, 数据可分性越高, 最大值对应的分类结果为最优聚类结果。
三、实证与结果
1. 板块分类效果评价指标。 对股票进行板块分类是为了方便构建投资组合以对冲非系统风险。 本文采用板块内部股票价格波动的相关系数和板块之间股票价格波动的相关系数来判断板块分类方法的有效性。
假设沪深市场一共有N只股票, 并将它们分成M个板块, 每个板块对应有Nm只股票, 则对于第i(i=1,2…,N)只股票, 设它属于第m个板块, 它与板块内外的相关系数分别按如下定义:
板块内:Pim= pij/(Nm-1), j≠i。 版块外:Qim= pij/(N-Nm), j≠i。 pij表示第i只股票和第j只股票之间的相关系数。 板块内部股票价格波动的相关系数Pm= Pim/Nm。 与板块外部股票价格波动的相关系数Qm= Qim/Nm。 平均板块内股票价格波动的相关系数P= Pm/M。 平均板块外股票价格波动的相关系数Q= Qm/M。 通过比较板块内外相关系数差值的大小, 可以评价板块分类方法的优劣。
2. 股票CGR图。 下面以平安银行(股票代码:000001)股票为例作展示。 图3是某财经网站的平安银行股票的K线图。
K线图按时间顺序展示股票的交易价格数据, 但作为聚类算法输入数据, 维数太大, 对聚类要求高。 通过混沌游戏表示算法处理股票日收益率数据, 得到平安银行(000001)股票的日收益率CGR图, 如图4所示。
混沌游戏表示算法将股票日收益数据以迭代形式绘制在正方形图上, 其落点严格按照时间顺序产生, 也展示了部分分形特征, 如平安银行的CGR图无论是从整体来看还是按分块来看, 其落点都具有向右下角集中的特征, 这个特征意味着平安银行的日收益数据落在B集合, 即(-2.04%, 0.391%)这个区间的频率很高。
3. 自适应仿射传播聚类结果。 将16维向量集作为自适应仿射传播聚类算法的输入变量数据集, 在Matlab中运行后得到从2 ~ 78共计77种类数情况下的各项指标, 包含每种类数对应的各只股票的类标、分类优劣评判指标Sil和Silmin的值等。 整理不同类数对应的Sil和Silmin指标值得到表1, 类数大于18类之后Sil和Silmin两个指标值都越来越小, 受篇幅限制, 不再罗列。
可以看到, Sil的最大值是0.3479, 最优聚类结果为两类, 考虑到Sil的最大值小于0.5, 表明聚类有一些重叠的情况, 在聚类结果指标Sil值较小的情况下, 应优先考虑最靠近两类的可分性, 故取指标Silmin最大值0.1973对应的聚类数5类, 参考其他行业分类都是超过10类的情况, 再取次高点0.1688对应的聚类数11类。
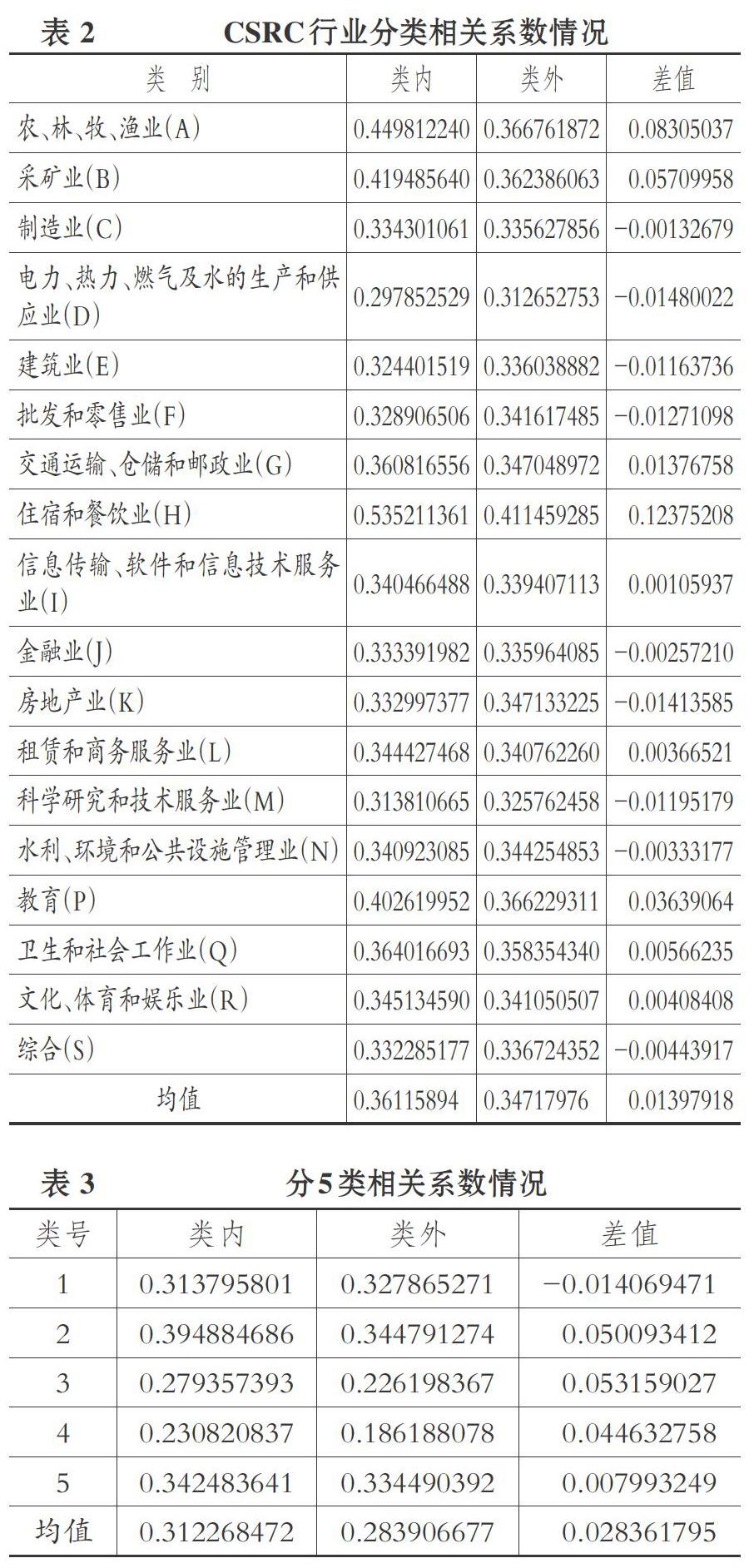
4. 板块内外相关系数的比较。 用证监会网站发布的2016年四季度上市公司行业分类结果分别计算类内和类外相关系数, 得到表2。
用本文的方法得到的分类结果分别计算类内和类外相关系数, 得到表3和表4。
分为5类时, 主要包括A、B、H、P以及其他类。 类内外相关系数差均值为0.028361795, 类内外相关系数差值较为明显, 仅一类存在类内相关系数小于类外相关系数的情况。 分为11类时, 主要包括A、B、H、P、D、E、G、I、N、R以及其他类。 相关系数情况如下:类内外相关系数差均值为0.026968596, 类内相关系数小于类外相关系数的情况增加。 整体而言, 无论是将所有股票分为5类还是分为11类, 类内外相关系数差均值都比证监会行业分类结果大, 区分度高。
从实际运用场景来看, 当股票投资者不需要对投资行业进行甄选细分, 仅对特殊行业进行统筹考虑时, 可以选用5类分析法进行分析; 当投资者需要进一步深入挖掘细分行业的投资机会或者行业特性时, 可以选用11类分析法进行甄选分析, 这样能够提高分析的精准度。
四、结论
本文以A股日收益率数据为数据源, 基于混沌游戏表示算法和自适应仿射传播聚类算法对我国A股进行板块分类研究。 利用生物信息学中的混沌游戏表示算法将股票日收益率数据转化为CGR图, 为股票数据展示提供了一种新的形式, 再对CGR图进行4×4的网格剖分, 将股票日收益序列转化为16维的向量, 降低聚类数据维度, 提高聚类效果。 通过自适應仿射传播聚类算法聚类得到新的A股板块分类结果, 与证监会行业分类相比, 类内外平均相关系数差别更大, 区分度更高。 本文提出的方法给股票板块分类提供了新的参考, 但仍存在一些不足, 本文主要侧重利用自适应仿射传播聚类算法对股票进行板块分类研究, 没有对通过混沌游戏表示算法得到的股票数据CGR图的分形特征进行深入研究。
【 主 要 参 考 文 献 】
[ 1 ] Kahle K. M., Walkling R. A.. The Impact of Industry Classifications on Financial Research[ J].Journal of Financial and Quantitative Analysis, 1996(3):309 ~ 335.
[ 2 ] Moskowitz T., Grinblatt M.. Do Industries Explain Momentum?[ J].Journal of Finance,1999(54):1249 ~ 129.

