直角扣件节点抗滑性能试验研究

朱 勇

(陕西铁路工程职业技术学院，陕西 渭南 714000)

模板支撑架体系是采用扣件将杆件进行连接而成的一种特殊的多层多跨空间框架，其中立杆与纵、横向水平杆使用直角扣件进行连接，而它们之间力的传递主要是依靠钢管和直角扣件间的摩擦力实现，因此钢管与直角扣件间的抗滑性能是一项重要力学性能指标，扣件抗滑承载力是保证扣件与钢管之间共同工作及有效传力的基础。目前，满堂支撑体系的节点半刚性计算理论比较符合扣件连接节点的实际情况，但是研究选取的对象多为新钢管和直角扣件间的抗滑性能，没有考虑实际的材料情况，本文选取工地上正在使用的钢管和扣件之间的抗滑性能作为研究对象，进行6组试验探究荷载和滑移之间的关系。

1 试验概况

1.1 试验材料

目前，国家规范《碳素结构钢》(GB/T700)规定用于支撑架体系的钢管材料为Q235级钢，规格为Φ48×3.5(mm)。目前，市场上供应的支撑架钢管的质量参差不齐，普遍达不到规范要求。本文使用电子称称量钢管质量，使用游标卡尺测量试验所用钢管的外径、壁厚。按照《钢管脚手架扣件》(GB15831-2006检查扣件的外观，扣件各部位没有裂纹，无砂眼，表面也无明显粘砂，螺栓无滑丝现象，选用扣件满足规范的要求，但有轻微的锈蚀。

1.2 试验设计

(1)肖炽[1]等发现扣件式钢管支架安装时40N·m的扣件扭紧力矩比较合理、有效。因此，试验方案确定2根互相垂直的钢管用直角扣件连接，使用扭矩扳手拧紧扣件以确保钢管与扣件间的扭动力矩为40kN·m，将200mm长的立管固定在高套管底座内，底座与压力试验机紧密固定。

(2)在300mm长的横管上架立传力装置和千斤顶、传感器。

(3)试验加载前，确保高套管、钢管-扣件试件、传力装置、千斤顶、传感器组成的试验装置固定。

(4)使用千斤顶匀速加载，加载速度控制在300～400N/s，连续采集施加荷载P以及相应的钢管竖向位移值Δ1和扣件竖向位移值Δ2。

(5)加载至荷载不再增加而滑移不断增加或荷载增加至20kN时，停止试验。

2 试验结果及分析

以下给出了4组试件的竖向力-横杆位移关系和竖向力-扣件位移关系曲线。

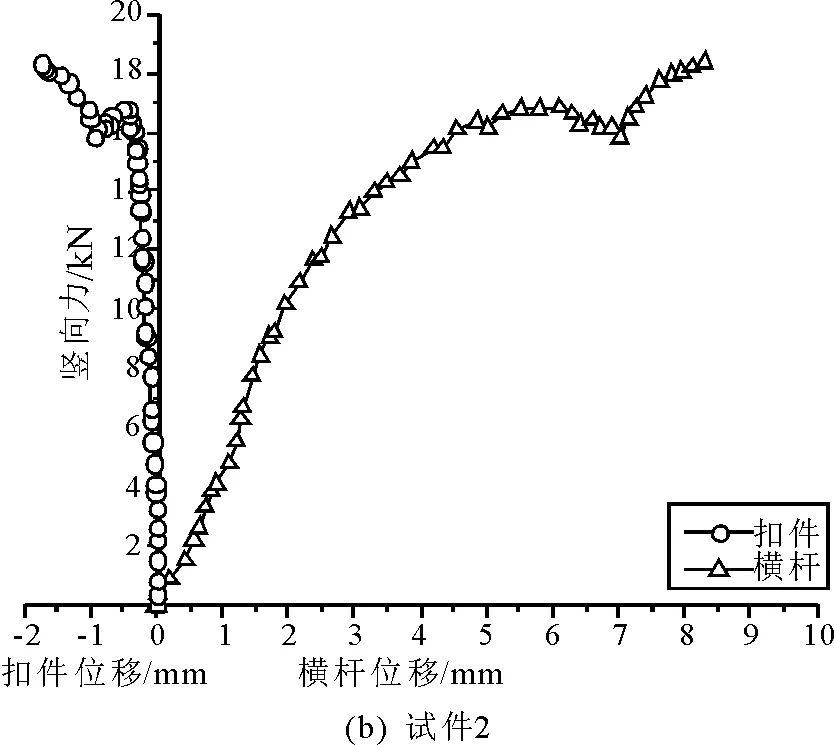
图2 钢管和扣件的荷载-位移关系

从图2看到：加载初期，随着荷载的增加，扣件位移和钢管位移线性增长，扣件位移向上增长较慢，而钢管位移向下增长较快，试验装置呈现典型的偏心加载受力特征；加载至一定值(约15kN)，曲线呈现2种不同的变化规律：一为随着少量的荷载增加，扣件位移向上、钢管位移向下快速增长，直至试件破坏；二为随着竖向加载的不断增大，钢管位移向下快速增长，而扣件位移也转向快速向下增长，直至试件破坏。

3 钢管脚手架直角扣件抗滑本构关系回归分析

在实际工程中，如果满堂支撑体系受到极大的突变荷载，造成某个关键部位钢管-扣件节点的滑动破坏，极有可能造成整个支撑架体系受力特征改变，继而引起其它钢管-扣件节点的快速失效，导致满堂支撑体系的倒塌事故[2]。因此，本文建立钢管-扣件间的荷载-滑移规律时，不考虑荷载增长极小而滑移快速增长的阶段。建立荷载P-滑移Δ曲线时，荷载取竖向荷载试验值，滑移取钢管位移⊿1和扣件位移⊿2的绝对值之和。

目前，对于钢管-扣件间的荷载-滑移关系曲线，国内外的拟合公式较少。本文分别采用二次关系式、对数关系式拟合本次试验结果。

P=AΔ2+BΔ+C

(1)

P=Dln(1+Δ)+E

(2)

式中：P为竖向力(kN)；Δ为滑移值(mm)；A、B、C、D、E均为待定参数。

本文分别采用这2种形式对实验结果进行拟合分析，相关参数的拟合结果见表1。

表1 P-Δ关系式拟合结果

将上述2种模型的P-Δ拟合曲线和试验结果进行对比，见图3所示。

图3 钢管-扣件P-Δ拟合曲线

由表1的相关系数和图3的对比结果可以看出：对数模型能更好地模拟试验结果，其对应的关系式为：P=6.553ln(1+Δ)-0.191

(3)

4 结语

加载初期，随着荷载的增加，扣件位移和钢管位移线性增长，扣件位移向上增长较慢，而钢管位移向下增长较快；加载至一定值(约15kN)，曲线呈现2种不同的变化规律：一为随着少量的荷载增加，扣件位移向上、钢管位移向下快速增长，直至试件破坏；二为随着竖向加载的不断增大，钢管位移向下快速增长，而扣件位移也转向快速向下增长，直至试件破坏。因此，水平横杆竖向承载力不应超过15kN。

在试验基础上，进行试验结果的回归分析，拟合出了竖向力-滑移值的公式，为使用有限元软件分析满堂支撑体系承载力和稳定性提供依据。

工地使用钢管和直角扣件前，应做竖向力-滑移试验，掌握材料的性能，对安全施工有较好的指导作用，建议在施工现场推广使用这种试验方法。