基于Panel Data的山地城市立交基本段通行能力影响因素研究

周约珥，龚华凤*，赵聪霄，徐小童，黄博亚

(1.林同棪国际工程咨询(中国)有限公司，重庆401121；2.重庆市山地城市可持续交通工程技术研究中心，重庆401121)

0 引 言

通行能力作为衡量道路最大承载力参数，是道路交通规划、设计与运营的重要指标.目前，国内对通行能力的研究不足，现行城市道路工程设计标准无法实现影响因素对通行能力的细化评估，必须参考美国Highway Capacity Manual(HCM)标准[1]，并考虑本地化的技术指标.此外，山地城市地形特殊，道路纵坡普遍大于3%，部分特大山地城市(如重庆)通常在主干道上修建互通立交，地方特征明显，难以通过现有影响因素量化指标，对通行能力进行科学准确评价.因此，研究山地城市立交基本段通行能力与影响因素间的量化关系，具有一定的现实意义.

通行能力可以通过交通流三参数模型计算，但无法反映道路几何线型、交通流组成等其他因素对通行能力的影响.因此，部分学者采用数值模拟等方法，对道路平纵几何线型、车辆类型，以及路侧条件等通行能力影响因素进行研究.针对平纵几何线型，刘江等[2]基于有效曲度和有效梯度的概念，分析公路的曲线半径和纵坡对通行能力的影响，发现当半径大于400 m 或道路纵坡小于3%时，道路平纵对通行能力几乎没影响.Hashim 等[3]通过对公路交通流数据的研究，建立通行能力与圆曲线半径等量化关系模型，当半径大于600 m时，通行能力不受影响.针对车道宽度因素，Khanorkar等[4]通过分析不同车型条件下车道宽度对通行能力的影响，认为车辆类型决定车道宽度对通行能力影响的强弱.对于路侧停车、公交站点等路侧因素，Munawar[5]提出路侧阻力的概念，建立通行能力分析模型，认为路侧停车是影响交通流运行速度、通行能力的主要因素.

综上所述，针对不同通行能力影响因素，既有研究考虑因素单一，忽视各因素间的相互关系，缺少对山地城市道路的考虑.因此，本文以山地城市立交基本段为对象，基于实测重庆市互通立交基本段交通流和道路线型等数据，研究山地条件下互通立交基本段通行能力的影响因素.

1 数据采集与预处理

1.1 数据采集

通过固定检测器与视频录像方式，采集重庆市7个主城区内14座互通立交基本段的交通流数据，约99.5×104条，覆盖重庆市各等级城市道路；通过车辆行驶过程中产生的GPS 数据与Civil 3D平台，获取道路平面与纵断面的几何线型数据.

1.2 数据预处理

固定检测器与视频录像获得的交通流数据，受调查环境影响，存在局部数据缺失或数据采集异常的情况，导致有效样本量降低等问题，故需要对采集的交通流数据进行数据挖掘与清洗等预处理.

(1)数据挖掘.

数据挖掘解决检测器漏检所导致的有效样本数减少等问题.交通流是典型的多元数据，故采用基于马氏距离的K 最邻近(K-Nearest Neighbor,KNN)算法[6]，对缺失数据进行挖掘补全.其中，马氏距离作为样本数据之间相似程度的定量描述参数，充分考虑了样本数据不同特性之间的联系，弥补了传统欧氏距离的不足.数据挖掘步骤如下.

Step 1马氏距离D为

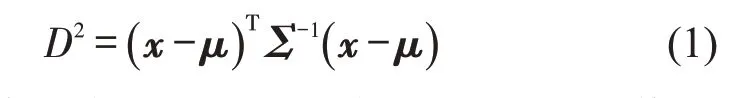
式中：x为单一路段的样本矩阵；μ为样本均值矩阵；Σ为协方差矩阵.

Step 2将(k+1) 条邻近数据的马氏距离进行归一化，得到pi为

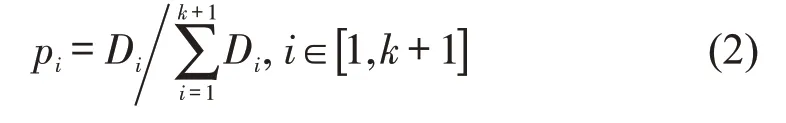
式中：k意指特征空间中第i条数据周边最邻近的k条样本数据，与第i条数据共同组成数据挖掘的数据基础.

Step 3第i个邻近数据的熵hi为

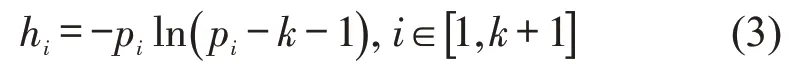
Step 4第i个邻近数据的变异系数vi为

Step 5第i个邻近数据的加权值wi为

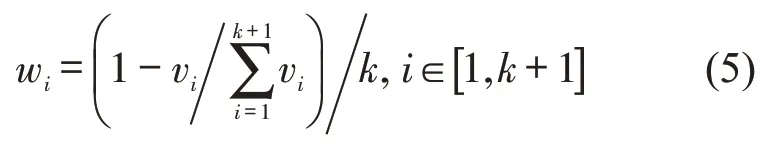
Step 6利用加权值对缺失数据进行挖掘修复，得到挖掘修复后的数据为

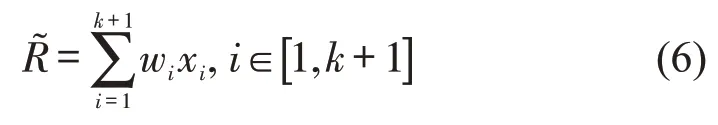
(2)数据清洗.

数据清洗解决检测器误检导致数据异常(离群值)等问题.基于数据挖掘结果，根据《数据的统计处理和解释正态样本离群值的判断和处理GB/T4883-2008》，运用马氏距离分别对1%和5%置信度下的离群值进行清洗.其中，小于1%置信度筛选得到的离群值为统计离群值，予以删除；1%～5%置信度筛选得到的离群值为歧离值，采用时间序列方法进行清洗.

预处理共删除总样本3.35%的错误数据，预处理效果良好.部分路段数据预处理效果如图1所示.

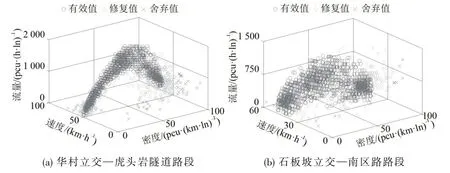
图1 数据预处理效果示意Fig.1 Example of data preprocessing

2 模型建立

2.1 Panel Data模型

Panel Data具有兼顾横截面数据和时间序列数据的特性，可有效分析不同时间、地点重复采集获得的多源数据，相比单一横截面数据或时间序列数据具有更高的应用价值.因此，基于Panel Data 对通行能力与各因素之间的量化关系建模，即

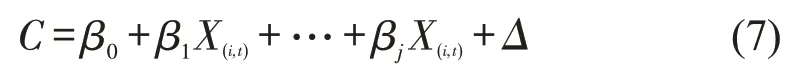
式中：C为基本段通行能力；i为互通立交基本段编号；j为模型中的自变量总数；t为时间序列；β0为个体效应，是一般常数项；β1～βj为模型截距，是建模中需进行标定的各因素系数；Δ为剩余变量，是一般常数项；X(i,t)为通行能力影响因素.

2.2 影响因素筛选

针对道路平面线型，基于刘江[2]、Hassan[3]等研究，考虑圆曲线半径与长度，平曲线转角与长度等通行能力影响因素.

目前，针对道路纵向线型研究尚未形成统一认识.Schwender[7]认为纵坡对通行能力的影响取决于交通流中大车比例，Zegeer[8]通过敏感度分析认为纵坡是通行能力的中低影响因素，刘江[2]认为只有当纵坡大于一定值时才会对道路通行能力产生影响.考虑到山地城市地形的特殊性，道路纵坡普遍较大，竖曲线前后坡差明显，受场地限制半径及长度普遍较小，故将竖曲线的半径与长度，竖曲线前坡，以及前后坡差等因素进行模型测试.

针对道路的横向线型，Hassan[3]和Zegeer[8]证明车道宽度和路肩宽度等对通行能力的影响较弱，为非主要影响因素，本文不予考虑.

除道路几何线型外，还考虑运行速度、设计速度、大车比例(城市中的大车以公交为主)、是否为匝道等因素.

综上，山地城市立交基本段通行能力影响因素如表1所示.

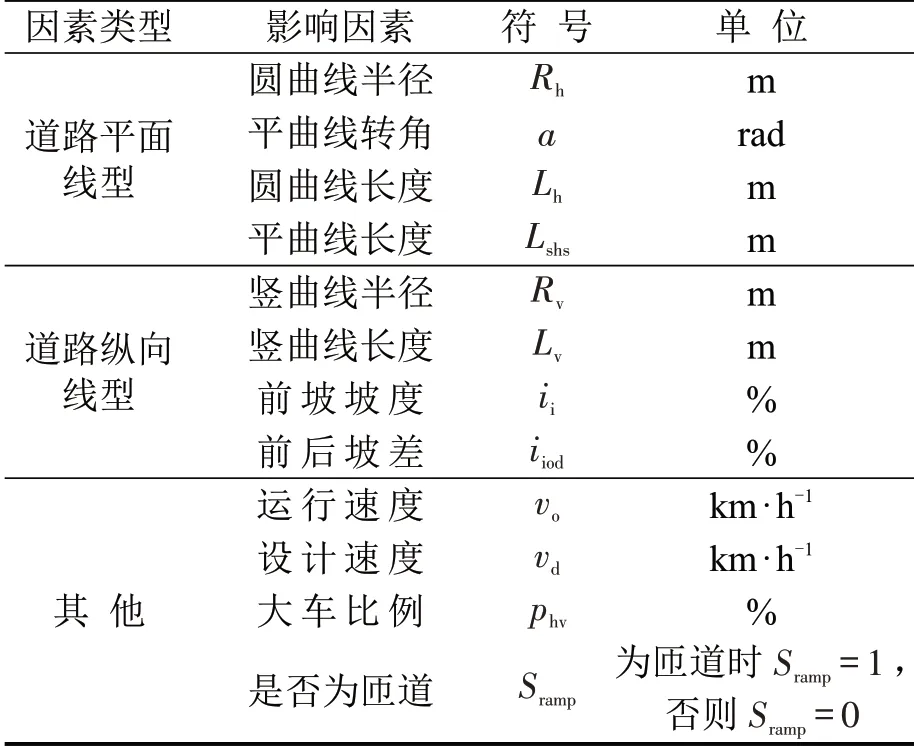
表1 Panel Data 输入因素Table 1 Input of Panel Data

基于表1与各参数特性，构建模型为

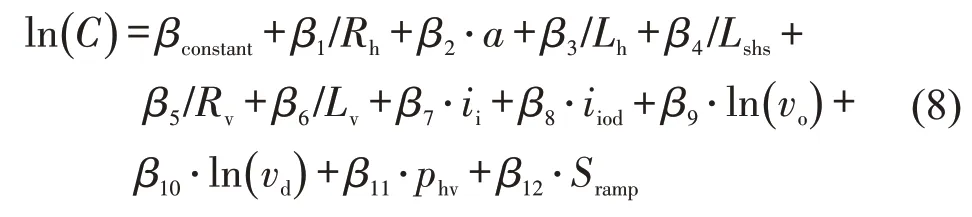
式中：β1～β12为各影响因素对应的待标定系数，即Panel Data模型中的模型截距；βconstant为常数项，是个体效应与剩余变量之和.

2.3 因素相关性分析

为筛除弱相关因素与干扰因素，采用Pearson检验对通行能力与各影响因素之间的相关性进行分析，结果如表2所示.

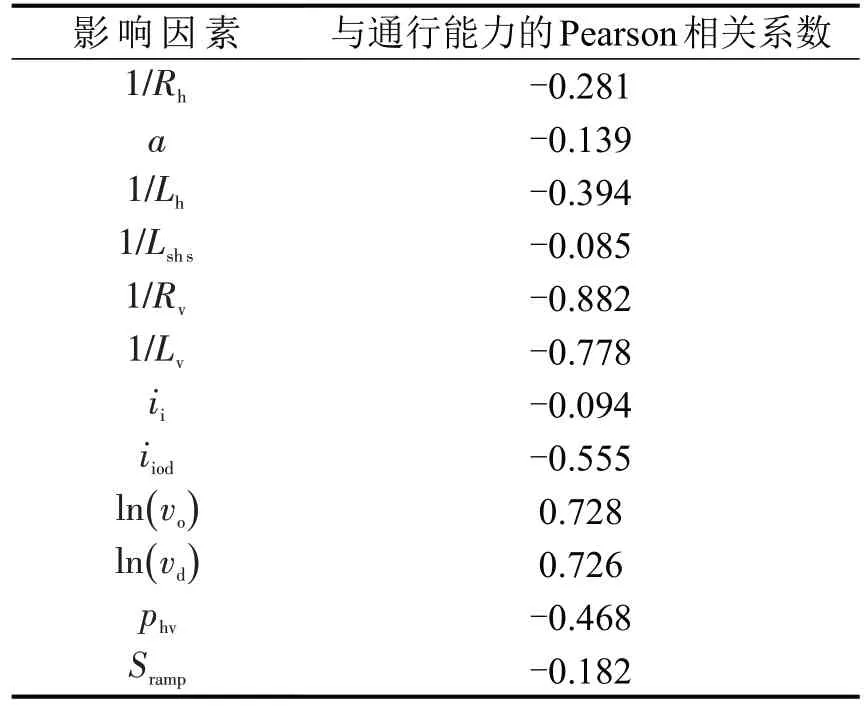
表2 Pearson 检验结果Table 2 Results of Pearson test

基于不同影响因素的Pearson检验结果可知：

(1)平面线型因素中，圆曲线的长度和半径是通行能力的主要相关因素.

(2)纵向线型因素中，竖曲线半径、竖曲线长度，以及前后坡差是通行能力的主要相关因素.竖曲线半径与竖曲线长度高度相关，相关性系数为0.878，故两者不能同时放入模型中分析.

(3)非道路几何线型因素中，运行速度、设计速度与大车比例是影响通行能力的主要因素.其他未提及的因素由于相关性较低，在建模中不再考虑.

表2 中12 个影响因素，与通行能力相关度高的是圆曲线半径与长度，竖曲线半径与长度，前后坡差，运行速度，设计速度，以及大车比例.

2.4 通行能力模型的建立与验证

为确保模型合理、可靠，针对不同时间、地点获得的路段数据集，按1∶1随机分为建模组和验证组，前者用于Panel Data 模型建立，以确定模型的合理性与各参数的显著性；后者作为Panel Data建模组的外部数据，用于模型的误差验证，以确定其可靠性与泛化性.

(1)模型建立.

在数据预处理结果与因素相关性分析基础上，基于Stata 软件平台与建模组数据建模.在5%置信度下，通过对上述主要因素进行排列组合，建立通行能力与影响因素关系模型，并根据模型的显著性检验P值，拟合优度R2等指标对模型进行筛选，得到相应的Panel Data模型为

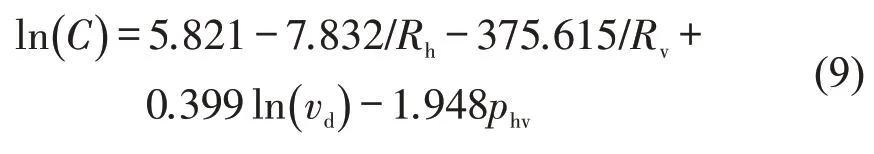
通行能力主要受圆曲线半径、竖曲线半径、设计速度与大车比例影响.模型的整体显著性与各参数显著性均表现良好，P值小于0.050，整体拟合优度为0.958，个体效应与平均干扰项误差之和为0.089，处于较低水平.模型检验结果如表3所示.

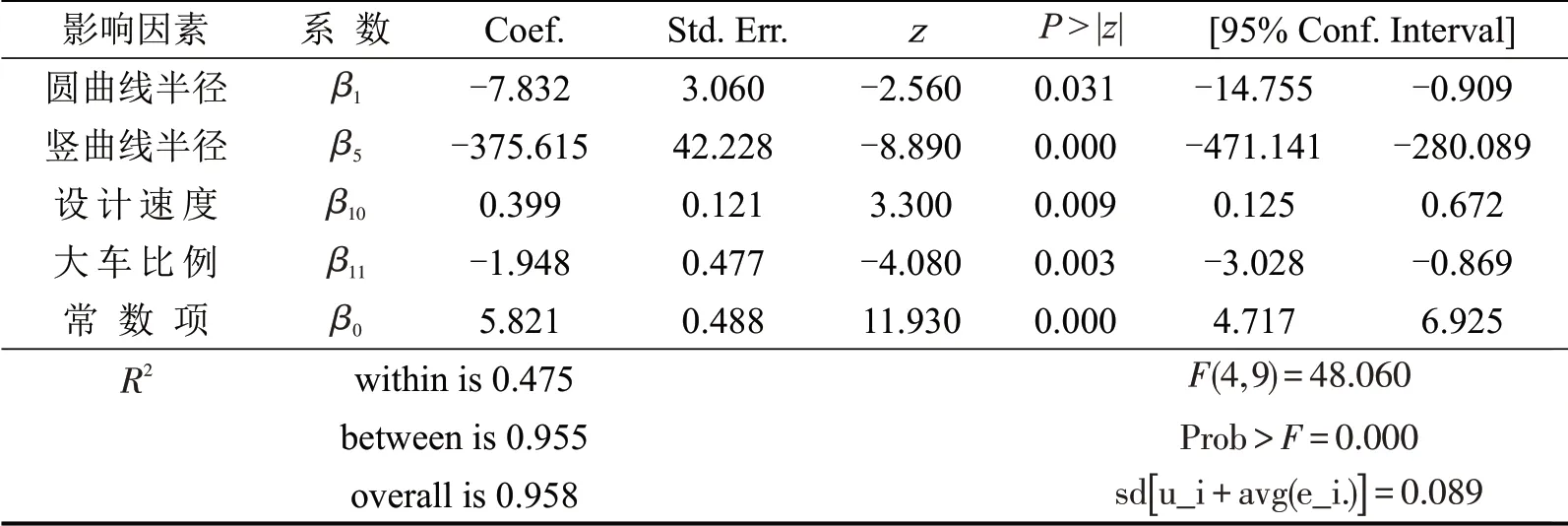
表3 Panel Data 建模检验Table 3 Panel Data modeling results

(2)模型验证.

基于验证组数据，计算模型与实测数据间的相对误差.例如，各路段通行能力与实测值误差的升序排列，如图2所示.

通行能力计算结果与实测值的误差均相对较小，平均相对误差为-2.998%，预测误差的标准差为7.961%，处于较低水平，故模型可以较好地反映主要影响因素与通行能力间关系.

图2 通行能力预测误差Fig.2 Prediction error of capacity

3 敏感度分析

为差异化区分不同因素对通行能力的影响，Zegeer 等[8]定义通行能力随单位影响因素变化的浮动百分比为敏感度，进而量化分析HCM中各通行能力影响因素.影响因素的敏感度小于10%时，为低敏感因素；敏感度介于[10%,20%]时，为中敏感因素；敏感度大于20%时，为高敏感因素.对Panel Data 模型中的通行能力影响因素进行敏感度降序排序，如表4所示.

基于敏感度，表4中各因素对通行能力的影响由大到小排列，依次为：竖曲线半径、设计速度、圆曲线半径、大车比例.

竖曲线半径决定行驶车辆的停车视距.山地城市道路普遍坡多、坡陡，前后坡差较大，竖曲线设置频繁.在竖曲线半径偏小的路段，停车视距较短，影响驾驶员对前方路况的判断，从而主动减速，影响路段通行能力.因此，通行能力随竖曲线半径的增大而增大，如图3所示.

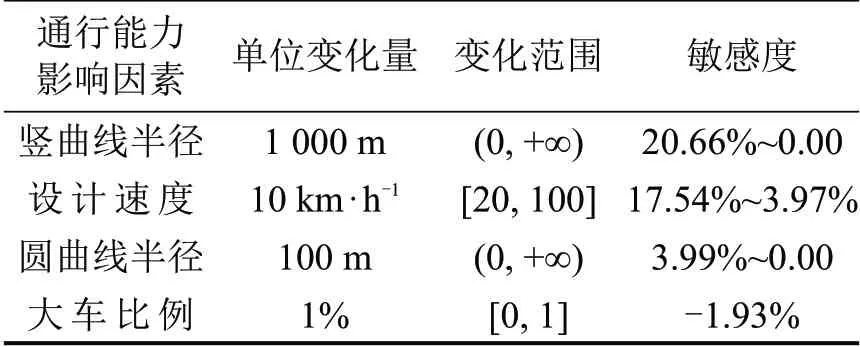
表4 主要影响因素敏感度降序排列Table 4 Descending table of main impact factor sensitivity

设计速度是与道路基本通行能力密切相关的基础参数，决定道路几何线型.设计速度越大，道路几何线型条件越好，运行速度越快，交通流的整体运行效率越高，通行能力越大.

圆曲线半径会影响驾驶员的驾驶心理与驾驶行为.在相同行驶条件下，圆曲线半径越小，离心力越大，行车视距越小，驾驶负荷增加，影响行驶车速，导致通行能力降低.因此，圆曲线半径越小，通行能力越小.如图4所示，当圆曲线半径为600 m时，通行能力下降1.30%.

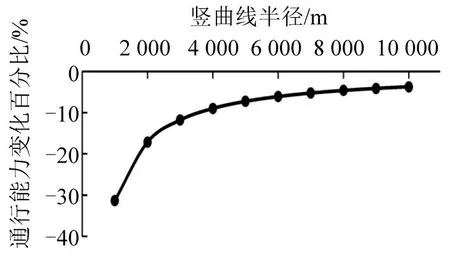
图3 通行能力与竖曲线半径量化关系Fig.3 Relationship between capacity and radius of vertical curve

图4 通行能力与圆曲线半径量化关系Fig.4 Relationship between capacity and radius of horizontal curve

大车比例是影响道路通行能力的重要因素.山地城市道路中的大车，主要为公共交通车辆，受自身车型条件、转弯半径、车辆性能等影响，行驶速度低且容易影响后方车辆视距，降低交通流的整体运行效率.因此，大车比例越大，通行能力越低，如图5所示.

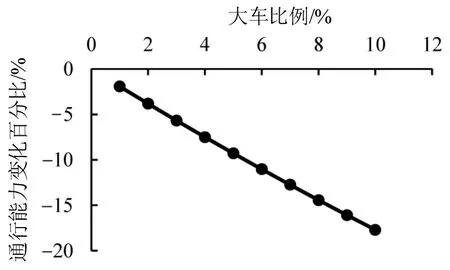
图5 通行能力与大车比例量化关系Fig.5 Relationship between capacity and percentage of heavy vehicle

大车比例每增加1%，道路通行能力降低1.93%.按HCM 2010标准[1]，在设计时速为100 km·h-1的道路上，1个车道的通行能力将降低41 pcu·h-1，影响显著.此外，道路纵向坡度作为山地城市的重要特征，被广泛认为是通行能力的独立影响因素.但在HCM[1]的最新通行能力计算方法中，坡度、坡长与大车比例被认为是共同作用的通行能力影响因素，不能独立考虑，仅当坡度小于2%时，道路通行能力不会随坡长与大车比例的变化而发生变化.山地城市(如重庆市)地形高低起伏，道路坡长普遍小于500 m，几乎不影响道路通行能力，可以忽略不计.针对坡度与大车比例，通过分析通行能力与坡度、大车比例的关系发现，大车比例对通行能力影响权重远大于坡度.若将大车比例替换为坡度，坡度的显著性检验P 值为0.210，影响不显著.因此，Panel Data模型将大车比例作为重要影响因素纳入模型，而不包含坡度因素.

4 结 论

经过统计学分析与检验，以12 种通行能力影响因素与实测通行能力数据为基础建立基于Panel Data的通行能力与影响因素关系模型，确定山地城市立交基本段通行能力的主要影响因素.通过敏感度排序，确定各主要因素的影响程度，由大到小依次为：竖曲线半径、设计速度、圆曲线半径、大车比例.与以往类似研究的结论不同，本文认为竖曲线半径和圆曲线半径是影响山地城市道路通行能力的主要因素，而非过去普遍认为的道路坡度.大车比例与道路纵坡作为共同作用的通行能力影响因素，在地形复杂的山地城市中，前者对通行能力的影响远大于后者，是研究山地城市互通立交基本段通行能力不可忽略的因素.