考虑区间重叠的多运营商公交调度优化

宋现敏，张明业，姜景玲

(1.吉林大学交通学院，长春130022；2.中国交通运输科学研究院，北京100029)

0 引 言

城市化建设速度不断加快，城市道路资源日益紧张，公共交通具有缓解交通拥堵、提高居民出行效率的作用，故大力发展公共交通成为各国的共识.关于公交线路调度的研究主要集中在公交发车频率和时刻表优化两方面.

公交发车频率优化方面：Ceder[1]基于乘客调查数据给出4种确定公交车发车频率的方法，两种基于站点数据，两种基于区间出行数据；Ferguson等[2]考虑低收入人群、弱势群体的出行特征，将公平性纳入公交频率设置问题；姚宝珍[3]将综合集成赋权法引入公交发车频率优化中，构建以企业费用和乘客费用最小为目标的发车频率优化模型；曹莲英[4]采用多目标演化算法求解公交发车频率模型，最终求得发车间隔的全局最优解.

公交时刻表优化方面：Palma 等[5]基于公交车数量，乘客时间延误费用和不同期望出行次数，构建公交发车时刻优化模型；窦雪萍[6]以公交网络内总换乘负效用最小为目标，构建公交时刻表鲁棒优化模型.近年有学者对重叠区间进行研究：洪豆[7]引出公交线路重复路段的概念，建立以乘客出行成本和企业运营成本最小的双层规划模型；汤茹茹[8]考虑多车型的影响，分别建立考虑区间重叠影响的大型车、小型车、多车型公交调度模型.

综上，现有公交调度研究并没有考虑公交线路由不同运营商运营的情况，同时这些线路有一定的区间重叠.因此，本文构建一个双层规划模型解决多运营商重叠区间的公交线路调度问题，由上层模型确定线路分配方案，下层模型确定各公交线路的发车频率和发车时间，应用NSGA-П(Nondominated Sorting Genetic Algorithm P)算法求解模型，并以长春市南关区北侧区域的公交线网为案例进行分析，实验结果验证了模型的有效性.

1 问题描述与建模

1.1 问题描述

本文建立一个双层规划模型对问题进行描述，上层模型指政府机构负责对公交线路进行分配，目标函数使公交乘客的总出行时间(包括行程时间和等车时间)最小；下层模型为各运营商各自利润最大，是一个多目标优化问题，变量是各运营商运营公交线路的配车数和发车间隔，多运营商公交调度优化过程如图1所示.

为简化问题，做出以下假设：

(1)每条线路由一个运营商运营，每个运营商运营不止一条线路；

(2)每条线路行驶路线不改变，仍然经过相同的站点；

(3)站点间客流量保持稳定；

(4)乘客均匀到达公交站点.

1.2 参数定义

设公交网络中有l个公交线路，g个公交运营商，参数定义如表1所示.

1.3 上层模型

政府机构通过优化线路分配方案，使乘客出行时间达到最小，运营商在政府机构确定的线路分配方案下，确定运营线路的发车间隔，追求自身的最大利润，线路分配方案为

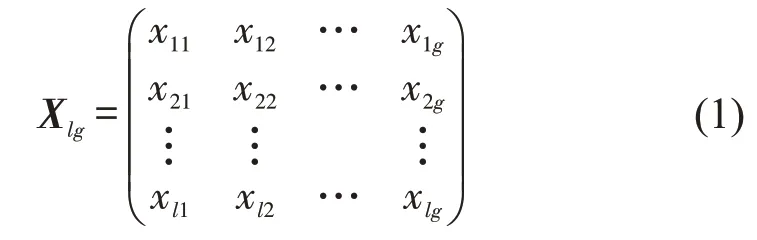
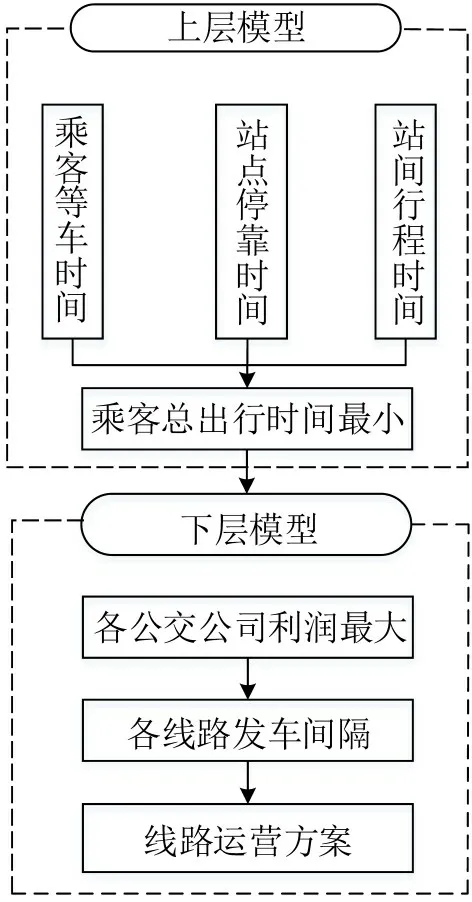
图1 多运营商公交调度优化过程Fig.1 Optimization process of multi operator bus dispatching

乘客总出行时间包括乘客在站点的候车时间和站点间的行程时间，通往(i,j)站点的乘客在站点i的平均等车时间为

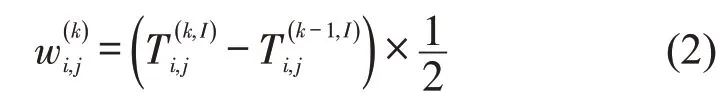
式中：由3部分组成，分别是车辆k驶离站点1的时间，OD站点(1,i)的路段行程时间和公交车在站点i之前(包括站点i)的公交站点停靠时间，即

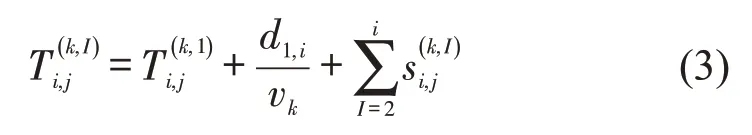
线路l内第n辆车的发车间隔为

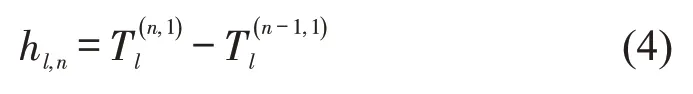
公交车在站点的停靠时间由乘客的上车时间和下车时间决定，取两者中最大值，即

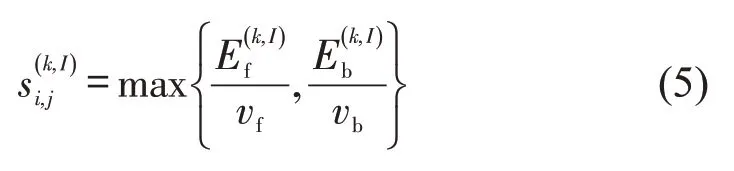
第k辆车在站点i下车的乘客数等于所有乘坐k车的终点站为i的乘客数，站点i的上车乘客数等于乘坐k车，且终点站为i+1 到m的所有乘客数，计算公式分别为

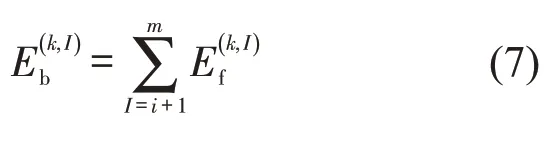
表1 参数定义表Table 1 Parameter definition table

乘客在(i,j)站点间的行程时间由(i,j)的路段行程时间和所有经过站点的停靠时间组成，即

公交系统内，乘客总出行时间由乘客在站点间的行程时间和等车时间构成，故本文构建模型为

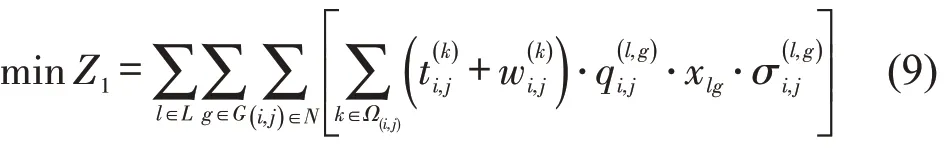
站点(i,j)内，选择由运营商g运营线路l的乘客数为

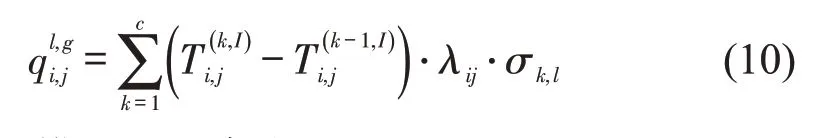
上层模型的约束为

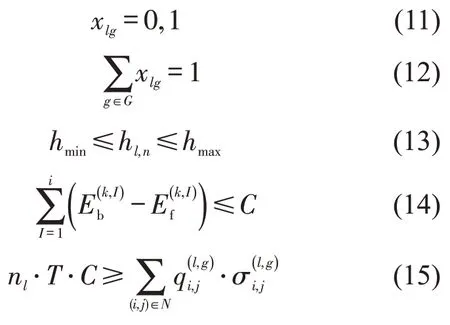
式(11)和式(12)表示每条线路只能由一个运营商运营，式(13)表示发车间隔约束，式(14)表示站点上车乘客数需要满足车辆容量，式(15)表示线路配车数满足线路整体客流量需求.

1.4 下层模型

下层模型为

式(16)表示各运营商追求自身利润最大化，运营商g在应用线路方案pg时的利润，为该运营商运营所有公交线路的利润之和，即

运营商g运营线路l的利润等于收益减去成本，即

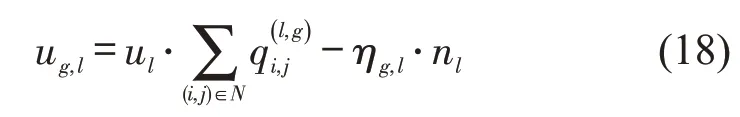
2 模型求解

上层模型中，将问题描述为一个0-1整数线性规划问题，隐式枚举法是求解这一类问题较好的算法，利用变量只能取0或l值的特性，进行分支定界，达到最优解.

下层模型中，由于各运营商都在追求自身利润最大，一个目标性能的改善往往是以损失其他目标性能为代价，故其解通常是一个非劣解的集合，即Pareto 解集.帕累托最优解指的是从一种分配状态到另一种分配状态时，在没有使任何人情况变坏的前提下，至少有一个人变得更好.换言之，下层模型中，各个目标之间会一直竞争直至达到一种均衡状态为止，而在其他运营商方案不变的情况下，帕累托解即是运营商能达到的最优解.

NSGA-II 算法(Elitist Non-Dominated Sorting Genetic Algorithm)是一种面对多目标优化问题的算法，具有运行速度快、解集收敛性好等优点，通常用于求解帕累托前沿解，本文求解步骤如下.

Step 1初始化，设定一个初始的线路分配方案.

Step 2在Step 1 确定的线路分配方案下，通过下层模型求解出相应的帕累托解集.

Step 3将Step 2得到的帕累托解集中的解分别输入到上层模型中，选择使上层模型的乘客总出行时间最小的线路方案，该方案即为对应线路分配方案的最优线路方案.

Step 4更新线路方案，重复Step 2和Step 3.

Step 5选择使乘客总出行时间最小的线路分配方案和线路方案，并输出实验结果.

3 案例分析

3.1 实验背景

选取长春市南关区北部区域公交网络内4 条公交线路进行分析，这些线路彼此有部分区间重叠，分别由两家公交公司运营，即南通公司和巴士公司，各公交线路信息如表2所示.

表2 公交线路信息表Table 2 Bus line information

客流数据采用人工调查方法，调查时间为晚高峰(16:30-17:30)，调查数据为各站点上、下车的乘客数.根据各公交线路在各站点的上车客流量及乘客站点下车概率表，推算各条线路的OD客流数据.参数设置如下：最小发车间隔2 min，最大发车间隔10 min，乘客上车平均速度2.5 s/人，乘客下车平均速度2 s/人，票价1 元，公交车运营成本2.07元/km，公交车平均运行速度15 km/h.

3.2 实验结果分析

对比分析优化前、后方案，优化前方案指现状调度方案，优化后为采用本文模型优化后的方案，结果如表3所示.

由表3 可知，优化后的乘客总出行时间为98 997 min，降低了5.93%.乘客的OD站点固定，同时假设公交车辆平均行驶速度固定，故乘客在站点之间的行驶时间固定，路段行程时间发生变化的主要原因是公交车辆在公交站点的停靠时间，共减少1 274 min；由于优化了线路分配方案及线路内各车辆的发车时间，乘客总等车时间下降27.56%，证明了模型的有效性.各公交公司在优化后的线路分配方案及相应利润如表4所示.

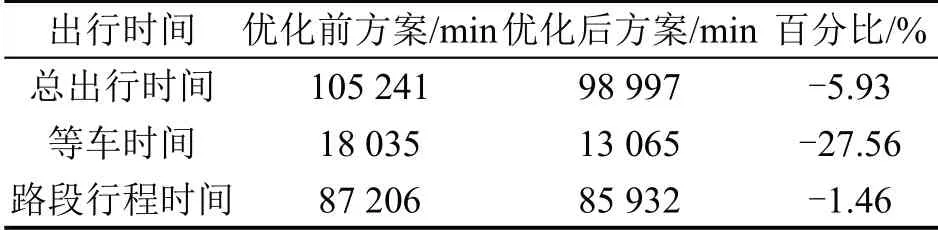
表3 两种调度方案对比Table 3 Comparison of two scheduling schemes

表4 运营商优化前后利润变化Table 4 Profit of operator before and after optimization

表4中，优化前后的利润是通过下层模型计算得到的，即线路的总收益减去线路总成本，收益为各条线路的票价收入，成本为公交车辆的运营成本.在优化后的调度方案中，南通公司分配到6 路和363 路的车辆数分别为18 veh 和6 veh，巴士公司分配到160 路和312 路的车辆数分别为21 veh和6 veh，优化后的公交发车时刻表如表5所示.

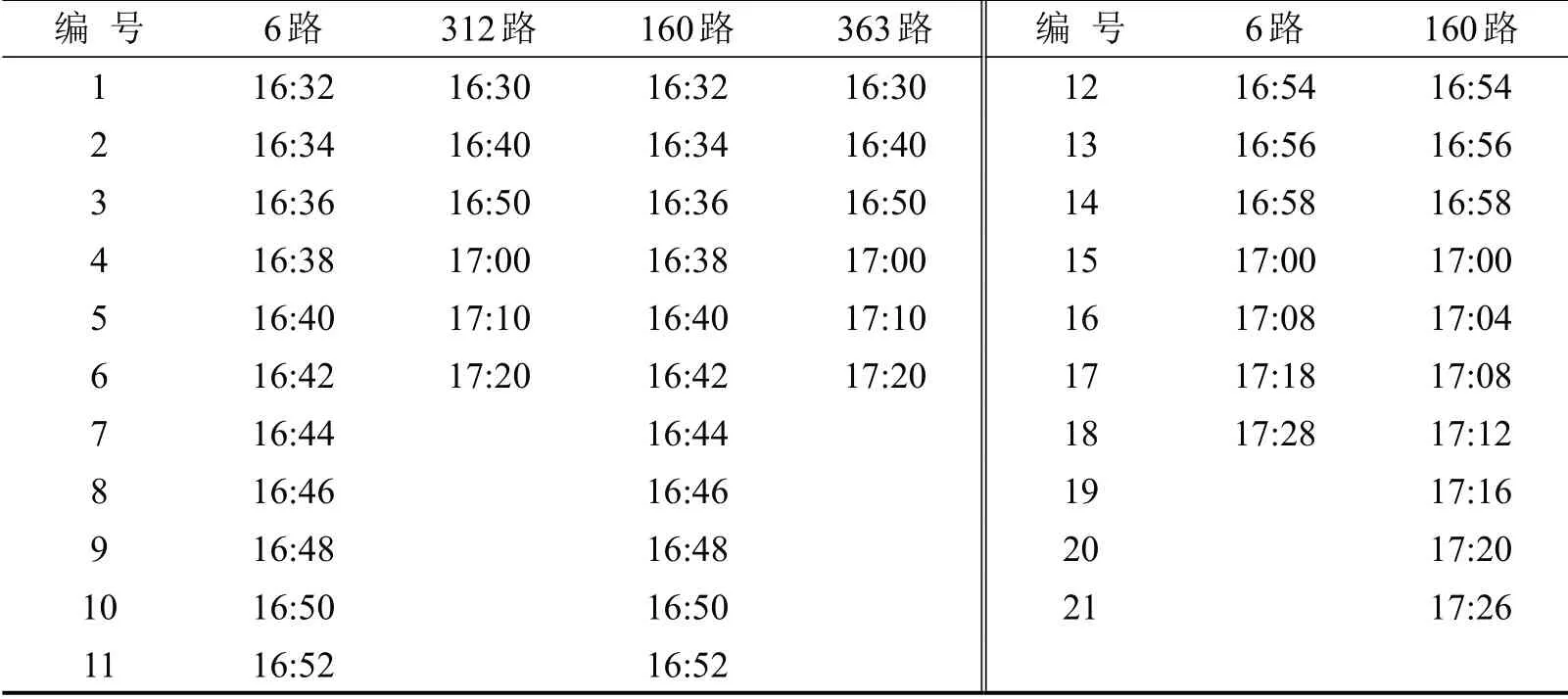
表5 优化后公交发车时刻表Table 5 Bus dispatching timetable after optimization

对于有重叠区间的多运营商公交线路调度问题，客流量的竞争主要体现在重叠区间，因此，对优化前后各条线路在重叠区间的客流量进行细致分析.

图2 横坐标为各线路重叠区间编号，共有46个重叠区间，纵坐标为各条线路的累积客流量.重叠区间的前部分，只有6 路和312 路竞争，两者车辆数在优化后都略有下降，故6路和312路在重叠区间23 之前变化幅度不大；在这之后，160 路参与竞争，同时160 路的车辆数增加较为明显，故160路在重叠区间的竞争力加大，优化后的累积客流量加大，而6 路的累积客流量有所降低，体现出调度方案变化对各条线路在重叠区间的影响.

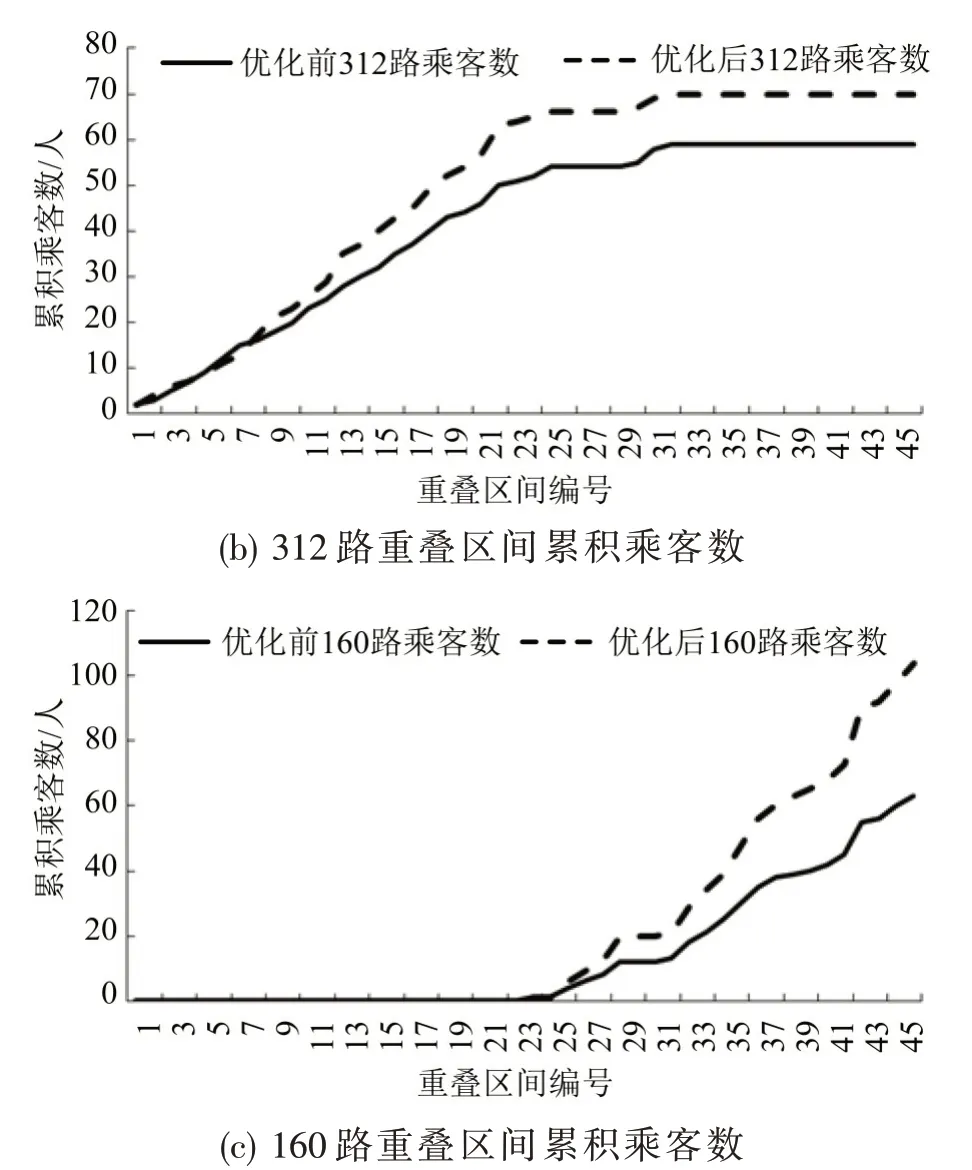
图2 各条线路重叠区间累积乘客数Fig.2 Accumulated number of passengers of each line in overlapping section

乘客对公交服务质量的最直观体验是等车时间，因此，本文对优化前后乘客在重叠区间的等车时间进行对比分析，如图3所示.

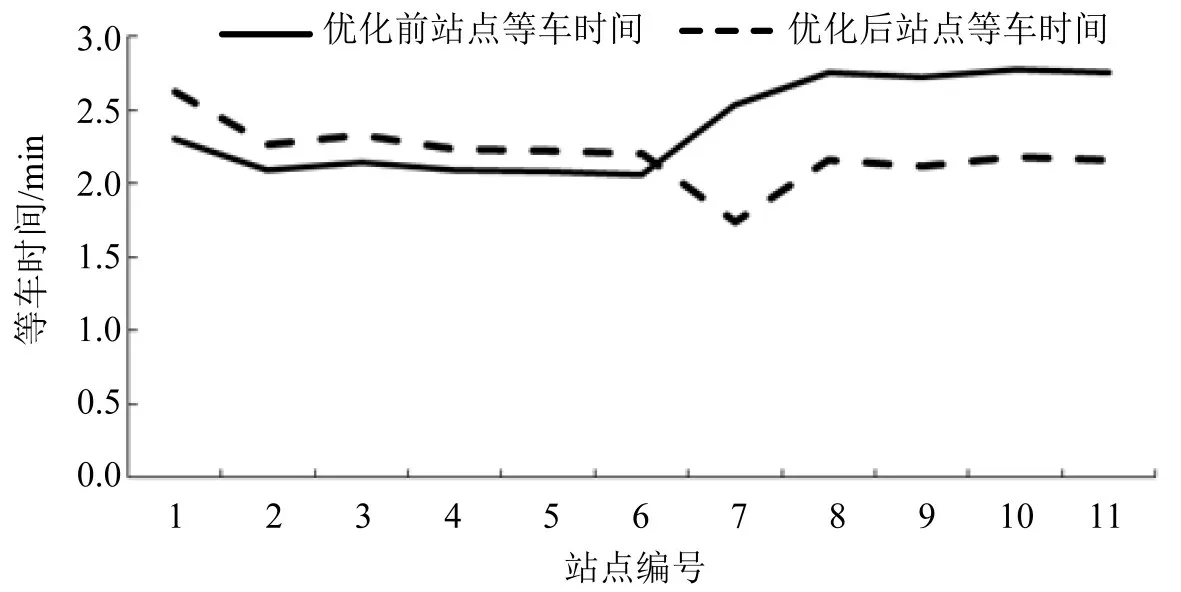
图3 优化前后重叠区间站点等车时间对比Fig.3 Comparison of waiting time at overlapping stations before and after optimization

由图3可得，站点1～6这6个站点，乘客可选择的线路为6路和312路，这两条线路在优化后配车数减少，故乘客等车时间略有增加；站点7～11 这5个站点，乘客可供选择线路为6 路，312 路和160路，因160 路的配车数有较大增长，乘客的等车时间大幅降低.

4 结 论

本文考虑各公交运营商在重叠区间的竞争因素，构建多运营商公交调度的双层规划模型，并选取长春市南关区北部区域的公交网络进行案例分析.研究结论如下：重叠区间内各条线路的乘客数和乘客等车时间与线路配车数和发车间隔有关，运营商可通过优化发车间隔以提高在重叠区间的竞争力.此外，应用本文模型对公交线网进行优化，公交乘客总出行时间降低5.93%，公交线网性能得到较大改善，验证了模型有效性.