基桩反射波理论和测试方法的发展与其核心思路

荣垂强

（广东开放大学工程技术学院，广东 广州 510091）

0 引言

近年来，基桩，特别是大直径基桩在建筑、码头和桥梁工程中被广泛使用，其施工质量直接决定了整体结构安全与否，对基桩进行无损的施工质量检测与评定，意义重大。

基桩反射波法（工程中常称为低应变法）检测用于评判桩身完整性，其最重要的目的是识别和定位桩身缺陷，该方法测试便捷、费用低，对结构无损伤，从而在工程中得到广泛应用，每年有百万计的基桩通过这一方法评判其施工质量，检测费用以亿元为单位。

目前，国内外关于基桩低应变法检测的研究主要有两种方法。一种是一维弹性杆的纵波理论，它是现有基桩低应变测试的理论基础；一种是三维理论，它因一维理论无法解释的三维问题与现象而发展起来。

1 一维理论

一维理论具有两个重要特征：①信号只包含纵波成分；②需要满足平截面假定，即满足任意深度横截面上的测点，其纵向运动的速度相同。

在国外，Smith［1］给出了应力波理论的差分方程，并成功实现了计算机程序求解，从而将应力波应用于工程桩的检测。Militano［2］通过积分变换研究了基桩在瞬态荷载作用下的动力响应。Rausch F［3］等用行波法计算并拟合实测桩顶速度时域曲线，获得了桩身波阻抗分布对信号的影响及其它成果。在国内，湖南大学的周光龙研究了基桩参数动测法［4］。陈凡采用特征线桩基波动分析程序分析桩基波动情况［5］。王奎华等［6］研究了变截面阻抗桩受迫振动问题，或得了其解析解，并对计算结果的应用进行了分析。刘东甲利用 Laplace 变换和矩阵理论，得到了纵向振动桩侧壁切应力的表达式，提出了桩周土的等效参数［7］，为通过低应变测试信号反演桩周土参数提供了较好的方法。此外，其它学者也开展了大量的研究工作。

上述低应变一维理论的研究为工程测试奠定了理论基础，而且，由于一维理论简单易懂，信号也相对简单明了。当桩径 ＜1.8 m 时，实测信号与一维理论的信号特征符合较好，故而该理论已被广泛接纳和应用。但是，随着桩径的增大，实测信号特征和一维理论出现了越来越明显的差异，这种差异称为三维效应，它主要体现为两个方面。

1）桩顶面不同测点存在高频振荡信号，由于一维理论只包含纵波，它无法解释这一高频振荡信号而将它误判为缺陷信号。

2）桩顶面不同位置的测点，三维干扰信号的强度存在显著差异，相位也可能相反，这与一维理论平截面假定中，任意深度横截面上各点的速度相同不符。

上述问题必须从三维角度开展研究。

2 三维理论

现阶段，基桩三维理论研究的重点是三维干扰信号的成因和相应的减小三维干扰信号强度的采样方法，如单点采样法和双速度采样法。研究的根本目在于通过采样方法消除非纵波成分，达到实现主要保留纵波信号而继续使用简单易懂的一维理论的目的。

2.1 三维干扰信号的成因分析

现阶段，常说的三维干扰信号专指信号中的高频震荡“面波”信号，针对这一干扰信号的成因，目前有三种解释。首先，一种解释是从波场分析的角度，陈凡根据数值模型的波场变化和实测信号的频域分析结果，提出三维干扰信号是表面波与剪切波在桩顶面的来回反射的耦合在一起的综合结果［8］；刘东甲计算模型计算得到的时域和频域信号则显示三维干扰信号主要来源于表面波在桩顶面的来回反射［9］；其次，另一种解释是从振动的角度，认为三维干扰信号起源于某一系列的振动模态［10-11］，其中，郑长杰等［10］采用的是简化的桩土半解析解模型，荣垂强等［11］采用的是纯桩模型的模态叠加分析。中国的基桩检测规范［12］也认为三维干扰信号可能来自于某一横向振动模态。再次，还有一种解释则是上述两种解释的综合体，柴华友［13］认为三维干扰信号来源于表面波在顶面的来回反射和轴对称轴向振动模态产生的合速度贡献。

2.2 采样方法

采样方法是在上述理论分析的基础上发展而来，其出发点为利用三维干扰信号沿径向的强度和相位分布特征，避免或消除三维干扰信号，具体可分为单点采样法（见图 1）和双点采样的双速度平均法（见图 2）。

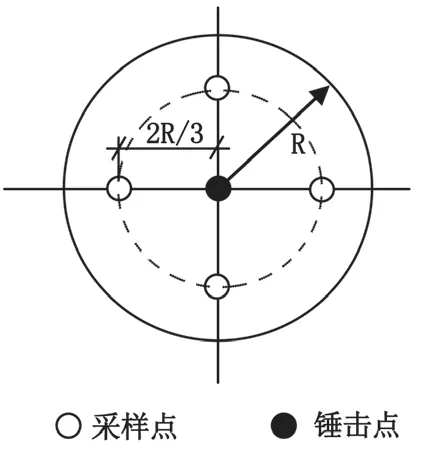
图1 单点采样法

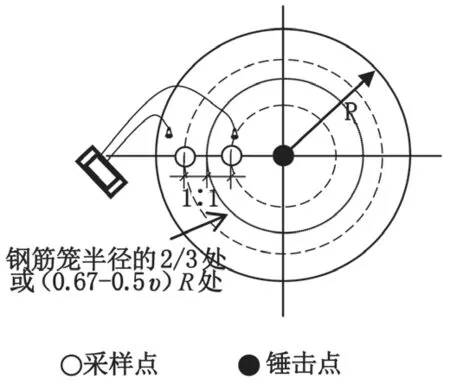
图2 双速度平均法

2.2.1 单点采样法

单点采样法利用单个探头在基桩半径上某一测点位置采样，实际上就是寻找基桩半径上的三维干扰信号最弱的点，不考虑不同测点三维干扰信号相位的差异。现阶段的相关研究中，关于三维干扰最小点位置的描述主要有三种形式。

1）最优测点位置单一且固定。根据参数分析，陈凡基于桩径 0.8 m 有限元模型，对比不同测点信号，提出三维干扰最小点位于 0.67 R（半径）处，刘东甲课题组有限差分法模型，提出三维干扰最小点位于 0.55 R 处，而 Chow Y.K 等［13］通过对比入射脉冲后部的负向信号的幅值大小，提出三维干扰最小点位于 0.5 R 处，这与业内将连续的高频震荡信定为三维干扰信号完全不同。上述研究给出的三维干扰最小点位置是一个具体的固定点位，且不同研究给出的具体点位也不同。

2）最优测点位于某一区段范围。Zheng C J等［10］基 于其提出的简化的半解析模型开展参数分析并提取相应数据进行对比，提出三维干扰最小点介于 0.5 R～0.7 R。柴华友等［14］基于其模型参数分析的计算结果，提出三维干扰最小点介于桩顶面半径的 0.5～0.75 R；他同时指出当特征波长大于 4 倍桩径，在泊松比等于 0.2 的条件下，在桩顶面 0.6 R 处的测试信号可以较好地符合一维条件下的测试信号特征。上述研究都未建立相关参数与三维干扰最小点位置之间的表达式，也未给出三维干扰最小点的几何意义。

3）最优测点位置为单一测点且位置随参数变化。荣垂强等采用有限元方法，通过参数分析研究了三维干扰最小点位置的影响因素［11，15］，提出了混凝土泊松比修正下的三维干扰最小点位置的函数表达式为 r/R=0.67-0.5 v，其中，v 为泊松比。对于混凝土泊松比未知的基桩，建议将钢筋笼半径的 2/3 处作为采样点位，这不仅修正了现有规范的采样点位置 0.67 R，同时后者还便于工人更直观地定位测点和打磨。当混凝土泊松比取值与前述不同学者相同时，这一函数表达式所得到的点位与他们提出的一致。主要参考陈凡的研究成果，并考虑到现场施工的便利，JGJ 106－2014《建筑基桩检测技术规范》规定检测点宜在0.67 R 处（见图 1），其它规范借鉴并采取了同样的规定。利用轴对称性，三维干扰最小点实际上为图 1 所示的虚线圆形上的任一测点。

2.2.2 双速度平均法

单点采样法只关注于定位三维干扰信号强度最小的点，并未利用同一半径上不同测点其干扰信号相位可能不同这一特征，利用这一反向位特征，得到两点采样的双速度平均法。

荣垂强等从模态叠加法出发，提出三维干扰主要来源于轴对称径向振动模态，并且发现该模态在桩顶表面的模态位移零点即为三维干扰最小点，从而解释了中心敲击下三维干扰最小点的几何意义。并且通过提取轴对称径向振动模态在桩顶半径上不同测点的模态位移，发现该模态在桩顶面位移零点两侧位移反向，且距离相同幅值相近。在速度上表现为，三维干扰最小点两侧近似等距离的两个测点，同一时刻，三维干扰信号的速度反向位且幅值相近。利用这一特征，可以通过两点采样并进行速度平均（见图 2）消除三维干扰信号，这便是双速度平均法。为了便于操作，这两个测点一般位于同一半径上，并需满足位于作为基准的分段线圆形（见图 2 箭头处）的两侧，且与分段线圆形近似等距离（见图 2）。当进一步考虑轴对称性，这两个测点的位置可以无需在同一半径上，即仅需分别位于图 2 探头所在的两个分段线圆形之上即可，测点的选择范围相对于单点采样法显著扩大。理论与实测信号均显示，该采样方法的平均信号稍优于单点采样法信号。

上述单点采样法和两点采样的双速度平均法，较好地避免或消除了基桩的高频三维干扰信号（面波信号），从而使得测试信号中主要保留了纵波信号，故而可以继续使用一维理论对测试信号进行评判。

3 结论

一维纵波理论简单易懂，更因其在桩径较小时与实测信号符合较好而被检测人员广泛接受。但当测试信号中出现强烈的非缺陷导致的三维干扰信号，该理论只能将它们误判为缺陷，理论失效。故而，现阶段三维研究的根本目的在于通过采样方法来消除三维干扰信号，实现主要保留纵波信号而继续使用一维理论的目的。基于理论研究提出的单点采样法和双速度平均法均很好地实现了这一目的，但它们的出发点完全不同。前者关注的是三维干扰信号幅值的强弱，通过在幅值最小的测点的采样来避免三维干扰信号，后者则是利用径向不同测点的三维干扰信号的相位可能相反这一特征并结合考虑幅值大小相近，将两个测点的信号进行平均，从而达到消除三维干扰信号的目的。