非连通通信网络中的分布式优化算法

王靖瑶 郭景华

0 引言

随着手机、电脑等电子产品的不断普及,IP视频流在现代网络中占据了越来越重的份额．思科公司年度视觉网络指数预测报告[1]指出,到2021年,IP视频流量在整个网络流量中的比重将会增长到82%,这远高于2016年的73%．此外,该报告还调研了用户对于视频发送服务的喜好,发现用户对服务的体验满意程度决定着用户对于服务商的选择倾向．因此,整个视频服务系统的成功运营不仅由它能否满足用户对视频服务不断增长的需求决定,还由它能否为用户提供满意的服务体验决定．然而,现存的网络资源分配协议却不能为视频服务系统的发展提供有力的支撑．这主要是因为:一方面,由于“大象流”的存在,现存的网络中网络资源分配不均现象频发;另一方面,用户对服务的满意程度函数作为数据率的函数,是非凹的.

自Kelly等[2]引入网络效用函数最大化问题以来,该问题框架已经被多次应用于网络资源分配协议及网络堵塞控制协议的研究．基于此问题框架的研究成果中,例如文献[3-5],大部分考虑的是由FTP和HTTP等应用产生的网络流,而这些网络流被认为是弹性流,其对应的网络效用函数是严格的凹函数．考虑弹性流的好处在于,所得到的最大化网络效用函数是容易求解的．但是,仅考虑弹性流却影响了上述研究成果在实际中的应用．这是因为,视频流和音频流被认为是非弹性的,并且被建模为非凹函数．例如,手机用户对视频服务的满意程度是一个关于数据率非减的并且阶梯状的函数[6].

视频和音频的这种非弹性特性逐渐被重视起来,文献[7]提出了一种中心式算法来逼近最优解,然而这种方法仅适用于优化可以转化成多项式形式的效用函数．文献[8-14]则提出了分布式算法．文献[8]针对效用函数为反曲函数的优化问题提出了求解次优解的启发式算法；文献[9]给出了在分布式梯度算法下收敛到全局最优解的条件；文献[10-11]针对连通通信模式下的互联网网络设计了分布式的流量分配方法,并通过仿真验证了算法对于链路断开的鲁棒性；文献[12-14]针对非连通通信模式下的互联网网络提出了分布式优化算法,该算法通过以流量目的地分类流量的方法更新数据率来减少计算量,但是由于算法运行需要传递较多信息,执行该算法仍需要较大的通信代价和计算代价.

本文针对非连通通信模式下的互联网网络,考虑了最大化效用函数的问题,将用户对服务的满意程度建模为非凹的函数．因而,本文要解决的是非凸的优化问题．本文的主要贡献有两方面:一方面,本文设计了一种分布式的流量分配算法来最大化网络资源利用率,并且避免了链路堵塞事件的发生;另一方面,本文设计的协议使得每个节点根据局部信息来决定自身发送数据率,需要的非局部信息仅仅是路径有没有堵塞的信息,而这个信息仅占一个字节(1 B).

1 预备知识

2 分布式流量分配算法

2.1 问题描述

本文将效用函数最大化问题建模为

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

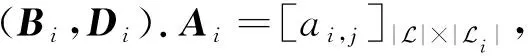
(10)

(11)

(12)

(13)

(14)

上述优化问题的限制条件是超空间和超平面的交集,该问题很显然是非凹的最大化问题．非凹的最大化问题是很难求解和分析的.

2.2 主要结果

注意到优化问题(10)是非凸的,这意味着该问题很难分析和求解．为了解决该问题,本文将用一类如下式的类多项式函数逼近效用函数:

(15)

基于上述逼近结果,有

(16)

(17)

(18)

(19)

(20)

类似于文献[10],将上述问题转化为下述等价问题:

(21)

(22)

(23)

(24)

(25)

(26)

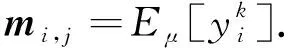
(27)

(28)

(29)

yi,maxM(1,l-1,mi)-M(2,l,mi)0,

(30)

(31)

(32)

(33)

(34)

(35)

对于类型为i的流量,pi=[pi,α]α∈{1,…,n}和mi=[mi,α]α∈{1,…,n}是矩构成的向量．yi,max是第i个数据率的已知上界．矩阵M(k,k+2h,mi)是如下式的汉克儿矩阵:

(36)

为了保持优化问题(27)的紧性,本文引入下述记号.

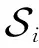
yi,maxM(1,l-1,mi)-M(2,l,mi)0,

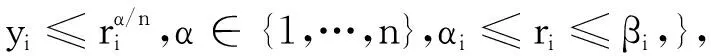
(37)

(38)

优化问题(27)可以写为

(39)

(40)

(41)

(42)

定理1优化问题(39)的解可以逼近问题(16)的解.

证明该定理的证明可由文献[10]中定理的证明得到.

接下来将求解凸优化问题(39).

(43)

(44)

这里,fi(mi,ri)是矩限制和上下限限制的指示函数,即:

(45)

g(x)同样是指示函数,即:

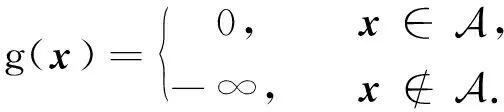
(46)

带有二次约束的拉格朗日函数为

(47)

基于ADMM的算法如下:

算法1 ADMM算法1)更新m和r:对于类型为i的流量,(mi,ri)更新:(mi,ri)k+1=argmax(mi,ri)∈ ipTimi-vi(ri-Tixki)-ρ2(ri-Tixki+uki)2 ,i∈ .(48)2)更新x:Txk+1=Π (rk+1+uk),(49)其中Π (·)代表了向集合 的欧几里得投影算子.3)更新u:对每个i∈ ,更新ui:uk+1i=uki+rk+1i-Tixki.(50)

注意到算法1中,x的更新步骤中需要全局信息,这就阻碍了将此算法应用于分布式场景．为解决上述问题,注意到投影意味着解决下述二次规划问题:

(51)

(52)

(53)

(54)

上述二次规划问题的等价问题为

(55)

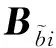
算法2 迭代算法 更新xi,1:对每个i∈ ,x(kg+1)i,1=x(kg)i,1-α(kg)(2(x(kg)i,1-(rk+1i+uki))+λ1βli+λ2γbi).(56)

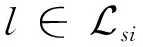
(57)

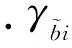
(58)

(59)

令数据率xi,j是由节点b经边l发出．βli代表了链路l的拥堵信息,即:

(60)

(61)

分布式算法如下:

算法3 分布式算法 1)给定初始值x0,u0,k=0,1,…,N.2)每个发送流量的节点通过求解一个凸的半正定规划问题更新它的数据率:(mi,ri)k+1=arg max(mi,ri)∈ ipTimi-vi(ri-Tixki)-ρ2(ri-Tixki+uki)2 ,i∈ .(62)3)给定初始值xkg,0←xk.4)kg=0,1,…,Ng,i=1,…,| |.5)每个节点b∈ i 查看它自身的流量守恒信息并且将γbi 发送它的最近的邻居.6)每条链路l∈ b 将它的拥堵信息βli 发给它相连的边节点, x(kg+1)i,1=x(kg)i,1-α(kg)(2(x(kg)i,1-(rk+1i+uki))+λ1βli+λ2γbi),(63) x(kg+1)i,j=x(kg)i,j-α(kg)(λ1βli+λ2γbi),j∈{2,…,| i|,(64) xk+1←xk,kg.(65)7)每个发送流量的节点更新它的对偶变量 uk+1i=uki+rk+1i-zki,i∈ .(66)

定理2算法3生成的序列{(mi,xi,ri,zi,ρui)}收敛到优化问题的一个KKT点.

证明该定理的结果可通过文献[15]中的结果得到.

3 仿真结果

考虑通信网络图2．网络中流量类型集合为S={1,…,8},并且多项式目标函数的阶数为n=6．算法参数为ρ=0.7,α(kg)=1/kg和λ1=λ2=8．图3比较了Ng=103时算法3和基因算法求解结果．从图3可以发现:虽然算法3是分布式的求解方法,但是该方法得到的目标函数值会收敛到基因算法这种中心式算法得到的全局最优解．这充分说明了算法3的有效性.

4 结束语

本文针对非连通通信模式下的互联网网络提出了一种分布式的流量分配方法．该方法可以有效地最大化网络效用函数,提高用户对服务的体验满意程度,并且避免网络中链路堵塞和流量丢失等现象的发生．仿真结果表明,虽然本文提出的方法是分布式的,但是该方法得到的结果可以收敛到原问题的最优解.