北京MST雷达功率谱密度处理算法改进

陈 泽 田玉芳* 吕达仁

1)(中国科学院大气物理研究所中层大气和全球环境探测重点实验室，北京 100029) 2)(中国科学院大气物理研究所香河大气综合观测试验站，香河 065400) 3)(中国科学院大学，北京 100049)

引 言

MST(mesosphere-stratosphere-troposphere，中间层-平流层-对流层)雷达根据大气折射指数不规则体对雷达发射电磁波产生的后向散射，获取对流层、下平流层以及中间层的大气三维风场及大气折射率结构常数等信息。可对3～25 km，60～90 km高度及以上大气层进行高时空分辨率探测，是研究大气多层区动力学特征与过程的独特手段。MST雷达的回波机制主要有3种：湍流散射、镜面反射以及热散射。大气湍流活动会造成大气折射率分布随机起伏，从而对电磁波产生散射，称为湍流散射，主要发生在对流层及以下大气层。大气中折射率水平分布较均匀，但在垂直方向上存在很大梯度，使用米波段或分米波段雷达探测该结构时，存在镜面反射机制，如对流层顶区。高层大气中离子、电子热运动形成的自由电子密度随机起伏，造成大气折射率不均匀分布，雷达电磁波产生的散射称为热散射，在中间层-低热层起作用。大气湍流散射是MST雷达回波的主要成因，有效散射体的空间尺度与入射电磁波半波长相当。MST雷达回波非常微弱，同时MST雷达目标信号也会受到本机噪声、地杂波以及间歇性杂波等影响。因此，从有干扰的弱信号中提取大气信号，需经过信号处理与数据处理。

国内外有关提高获取目标信号能力和处理信号的谱分析方法已取得一些进展[1-16]。目前北京MST雷达存储的原始数据是经信号处理后的雷达功率谱密度，在此基础上改进数据处理算法既可提高实时观测数据质量，也可提高历史数据质量。

功率谱密度中存在的噪声与其他杂波，对目标信号(晴空大气湍流信号)提取有很大影响。数据处理算法的理论基础可概括为大气风场在空间与时间上具有一定连续性和不同类型的信号在功率谱密度图上性质不同，如最大链检测法[17]、高斯拟合判断[14]、NIMA方法[18]与综合识别法等[19-26]。此外，还有研究通过抑制降水[27-28]、地杂波[29]等干扰信号以提高水平风场数据质量[30]。由于技术限制和算法本身的复杂性，有关数据处理的研究有限。值得注意的是，数据处理结果对噪声电平估算[31-34]准确性十分敏感，噪声电平估算是雷达数据处理过程中的一个非常关键步骤。

当前北京MST雷达数据除了风场数据，其他数据产品未得到充分应用，主要因为雷达数据处理系统所使用的算法仍需要改进。如噪声电平估算明显偏小，未能对目标回波进行精确识别，杂波干扰未被有效抑制，虽然对一阶矩(多普勒速度)影响较小，但会导致零阶矩(回波功率)与二阶中心矩(谱宽)的值偏大。因此，本文将从噪声电平估算与目标回波准确识别与提取两个方面改进，在噪声电平估算过程采用对数-线性拟合方案实现客观分析法，以提高实时观测与历史观测数据的质量。

1 数据及北京MST雷达简介

1.1 数 据

本文使用北京MST雷达数据、北京探空数据和ERA5再分析数据。

北京MST雷达数据：选用2012年1月1日00:00—12月31日23:59(世界时，下同)的中模式数据，每30 min探测1次，垂直分辨率为600 m。

北京探空数据：选用2012年1月1日—12月31日北京市观象台探空的水平风场数据，每日两次探测，探空球施放时间为11:15与23:15，每1～2 s记录1次，垂直分辨率约为10 m。为方便计算，将探空数据插值成垂直分辨率为50 m的数据集。

ERA5再分析数据：选用2012年1月1日00：00—12月31日23：00单点(39.75°N，117°E)模式高度层的垂直速度数据，时间分辨率为1 h。将垂直速度线性插值为垂直分辨率为600 m的数据集，与北京MST雷达数据高度相同。

1.2 北京MST雷达

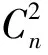
2 MST雷达功率谱密度处理算法改进

MST雷达信号并非只有目标信号，还存在非目标信号，因此对功率谱密度进行处理，精确提取目标信号是一项必需的工作。MST雷达信号可分为两大类[37]，即大气要素与非大气要素信号。大气要素信号包括晴空大气湍流、降水等，非大气要素则包括地杂波(如地面的建筑、山、树等造成的信号)、间歇性杂波(如飞机、鸟类的飞行等所造成的信号)和系统噪声等。当以大气湍流为探测目标，则噪声、间歇性杂波等非目标信号常对基础数据估算有很强干扰。

2.1 噪声电平估算

在功率谱密度图中，一般认为高于噪声电平的每个包络均对应着信号。因此噪声电平估算的准确性不仅对SNR估算有重大影响，同时在信号提取中也有重要作用。

为抑制直流与窄而强的回波信号的影响，在处理功率谱密度前需进行预处理，包括零频去直流以及三点平滑处理(如图1所示)。

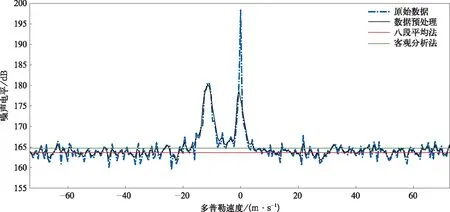
图1 2012年1月4日00:10北京MST雷达原始功率谱密度及数据预处理叠加经客观分析法和八段平均法处理的噪声电平(15 km高度东波束)

估算噪声电平时，最常用的方法是Hildebrand等[31]提出的客观分析法。客观分析法的基本原理是假定雷达测量的噪声信号属于高斯白噪声，将功率谱密度在某个待定噪声阈值以下的点组成该距离库的噪声功率谱密度序列记为{Sm}，频率范围为F，第m点对应的频率为fm(m=1,2,…,M)，通过调整预置的噪声阈值，当噪声功率谱密度序列计算出的方差与高斯白噪声理论给出的方差相等时，该预设噪声阈值即为所求噪声阈值，该序列{Sm}的平均值即为噪声电平。Hildebrand等[31]根据高斯白噪声的均匀分布与高斯分布两个特征，给出如下两个方程组:

(1)

(2)

其中，fm为第m点对应的频率，共有M个点，{Sm}为噪声功率谱密度序列，F为频率范围，p是数据预处理时滑动平均的点数，如果不进行滑动平均处理，则p=1。

通过调整预设噪声阈值，当R1=R2≈1时，即得到所需噪声阈值。实际应用中，常规方案的噪声阈值预设从该距离库中功率谱密度最大值Smax开始向下搜索，将Smax与预设噪声阈值之差(dP)作为自变量计算R1和R2。R1从大于1的值开始以不规则方式逐渐接近1，而R2从小于1的值开始逐渐增大到1以上(详见文献[31]中图2b)，可见R2=1可作为确定噪声阈值的循环终止条件。以上客观分析法的基本原理与实现方法可参考Hildebrand等[31]和胡明宝[20]的相关工作。

由于客观分析法的实现存在一定难度，实际应用时多采用分段平均法。该方法是基于噪声服从自由度为2N/k的χ2分布的假设，将FFT(fast Fourier transform)点数为N的频谱均分为k段，每一段数据计算其均值，将最小的平均值视为整个频谱的噪声电平值。根据Petitdidier等[32]的研究，当k=8或k=16时效果最佳，实际使用一般取k=8，称为八段平均法。该方法算法复杂度低，易实现，且较以低于峰值10 dB或15 dB 作为噪声阈值估算噪声电平值的方法更客观[33]。

经过比对客观分析法与八段平均法的估算结果，发现八段平均法计算的噪声电平较低(图1)。对八段平均法，在功率谱密度图上，高于噪声电平的某些包络会出现多个极大值，其中部分代表噪声信号的包络谱宽值异常偏大，不利于后续处理，而客观分析法在此方面明显优于八段平均法。

客观分析法通过从功率谱密度最大值不断向下调整噪声阈值估算噪声电平，算法实现耗时长，选取合适的调整步长比较困难。为了快速实现客观分析法，本文使用两种方案，即对数-线性拟合方案与二分法方案。

二分法方案基本思路：对于某距离库的功率谱密度，当预设的噪声阈值取功率谱密度最大值Smax时计算的R2<1，即目标信号未淹没于噪声；接下来若预设的噪声阈值取八段平均法计算出的噪声电平Nk=8，通常计算出的R2>1，即实际噪声阈值在Smax与Nk=8之间。因此可将Nk=8和Smax作为预设噪声阈值的初始上下边界值，通过二分法(也称折半法)缩小噪声阈值的搜索区域，达到快速实现客观分析法的目的，该方案与客观分析法常规方案的原理完全一致，是一种常规方案。

在实际计算过程中，对大量距离库功率谱密度处理时发现，R2随dP增长呈类似指数变化趋势，若将lgR2与dP做线性拟合，则当lgR2=0时，对应(Smax-dPlgR2=0)为所求噪声阈值(图2)。由于图2b中lgR2=0时对应的dP与图2a中R2=1所对应的dP值相同，因此可以考虑应用先取对数再进行线性拟合的方案实现客观分析法，确定噪声阈值并估算噪声电平，具体步骤：①dP选取计算序列，计算对应的R2值；②对lgR2与dP进行线性拟合，当lgR2=0时所对应的dP为目标值，(Smax-dPlgR2=0)为噪声阈值；③根据所得噪声阈值，选取噪声序列，计算此序列的平均值即为噪声电平。

图2 2012年3月16日15:10北京MST雷达观测数据的R2及lgR2随dP变化

为进一步检验对数-线性拟合方案的有效性和可靠性，利用北京MST雷达2012年5月7.8～12 km 高度共1715个距离库的功率谱密度，分别采用对数-线性拟合方案及二分法方案估算噪声电平值并进行比较(如图3所示)。结果表明：对数-线性拟合方案估算的噪声电平与二分法方案估算值有很好一致性，二者差值的标准差、平均绝对差值与相关系数分别是0.43 dB，0.21 dB与0.998，前者的平均值为168.6 dB，后者的平均值为168.5 dB，表明对数-线性拟合方案可行有效。

图3 2012年5月北京MST雷达7.8～12 km高度内(1715个距离库)功率谱数据应用对数-线性拟合方案与二分法方案估算噪声电平对比

相比二分法方案，对数-线性拟合方案具有明显优势：①能够快速且准确估算噪声电平值。对数-线性拟合方案不需要预设参数，而二分法方案或Hildebrand等[31]方案，需要提前设定参数，且计算结果与计算速度对参数设定十分敏感；②对数-线性拟合方案可判断各距离库能否提取出噪声以外的目标回波信号，即当拟合直线的斜截距，即预设噪声阈值选取功率谱密度最大值时对应的lgR2>0时，目标信号淹没于噪声中，该距离库将不进行下一步的目标识别处理。而分段平均法则无法进行该判断。因此本文提出的对数-线性拟合方案快速实现客观分析法估算噪声电平是雷达功率谱数据处理过程中的重要改进，具有实际应用价值。

2.2 目标回波识别与提取

功率谱密度进行预处理后，需要进一步识别并提取目标回波信号。根据目标信号在功率谱密度图中的特点，将峰值最大、谱宽最大与功率最大的峰区称为三峰[22-23]，目标信号通常存在于三峰，视此三峰为对应距离库上的准目标信号。本文实现目标信号的识别与提取的步骤：①提取所有回波；②在所有信号中确定三峰为准目标信号；③以三峰为主链进行链式检验，对整个距离库进行目标信号的识别；④对称性检验，进一步抑制干扰信号；⑤根据地杂波对应的峰区特点对其进行抑制，最终准确识别和提取出目标回波。

2.2.1 信号提取

为提取目标信号，应当识别功率谱中所有信号。以噪声电平为阈值，将功率谱中大于阈值的每个峰区视为有效信号(Si)。首先识别每个峰区的极大值(Ci),再识别每个极大值左右两侧的极小值或噪声电平作为峰区的左右边界(li,ri)，则Si=Si(li,Ci,ri)。

2.2.2 链式检验

Clothiaux等[17]以链最长以及功率谱值之和最大为原则，提出最大链检测法进行目标回波信号的识别与提取。基于大气水平风场具有时空连续性，且雷达以大气折射指数不规则体，即大气湍涡为探测目标，作为大气风场探测的示踪物，使雷达能够探测到这种时空连续性的特点，结合最大链检测法以及三峰的概念，本文应用链式检验的方法进行目标回波识别。

某距离库中干扰信号比目标信号更强的情况在实际观测中较为常见，为了尽可能识别弱的目标信号需进行链式检验增点处理。经此处理后仍可能存在具有一定连续性的干扰信号，为抑制此类干扰信号需进行链式检验减点，步骤如下：

第1步，以判断径向速度梯度以及信号谱宽比值大小的方式实现链式检验增点。基于雷达某一波束所有距离库，将所有三峰视作准目标信号。计算某距离库中每个信号与其相邻两个距离库中所有准目标信号的径向速度之差以及谱宽之比，即该距离库中每个信号对应多个径向速度差值以及谱宽比值。将每个信号对应的每个径向速度差值与当地特征值进行比较，当小于当地特征值数量大于1时，继续下一步的处理，否则视为非目标信号。径向速度之差的特征值由北京探空数据确定，且径向速度梯度特征值的精确度对此步骤的影响很小。判断谱宽比值的大小，小于某一阈值时则视此信号为准目标信号。在处理北京MST雷达数据时，谱宽比的阈值取0.5时效果好。进行谱宽大小的判断是因为若仅以径向速度差值为判断标准，噪声信号有很大干扰；由于噪声信号谱宽比其他信号谱宽偏窄，因此可通过增加谱宽大小的判断实现链式增点的同时达到噪声信号抑制的目的。经过链式检验增点处理后，得到的准目标信号则主要包含目标信号以及有一定空间连续性的杂波和降水信号等。

第2步，以判断连续信号链上下两端距离库与各自相邻距离库准目标回波信号的径向速度差值大小的方式实现链式检验减点。经过链式检验增点后，将准目标信号连接成链，在某些高度范围可能存在多条链。对于具有空间连续性的非目标信号所连接成的链，通常仅在链的两端存在极大的多普勒速度变化，即链两端距离库与各自临近距离库的径向速度差值有异常大值，而目标信号链在整个波束探测的距离库范围内连续，不存在这样的特点，据此可以将非目标信号的链剔除。实际应用时，计算某一距离库中某一准目标回波信号的径向速度与上下各3层(共6层)距离库中所有准目标回波信号的径向速度差值，并记录径向速度差值绝对值的最小值，共有6个正值的序列。当此序列的方差过大或值异常偏大的点数大于2，则认为此信号为非目标信号。径向速度差值异常偏大的判断标准是与当地特征值进行比较，又因异常偏大值远大于当地特征值，因此径向速度梯度特征值精度对此步骤影响很小。本文算法以大气晴空湍流为目标信号，在后续研究中，也可以对其他信号链进行提取，如降水造成的信号[38-39]。

2.2.3 对称性检验

对于具有五波束的MST雷达，其中东西波束和南北波束的方位角夹角均为180°，假设大气水平风场均匀，则认为对称波束在同高度距离库上测得的径向速度具有对称性。探测数据也证明各对称波束的目标信号几乎均关于原点对称。

经过链式检验后，仍可能有噪声与地杂波等非目标信号残留,可利用对称波束回波信号具有对称性的特点，通过对称性检验继续抑制剩余干扰信号。

同链式检验相比，虽然对称性检验也能抑制间歇性杂波以及降水信号等不具有对称性的回波信号，但实际情况中对称性检验有一定局限性，如链式检验能很好抑制噪声信号，而直接进行对称性检验则无法抑制噪声信号;当对称波束中一个方向缺测时，无法进行对称检验;垂直波束无法使用对称性检验。因而链式检验是必不可少的前提工作。

2.2.4 地杂波抑制

对称性检验对地杂波具有一定抑制作用，但仍可能有地杂波残留，如对称波束均有地杂波干扰时，无法通过对称性检验抑制地杂波干扰。基于高斯拟合判断的思路，根据地杂波在零频附近以及谱宽较窄的特点，可对残余的地杂波再做抑制处理。

经数据处理后的东西波束5个距离库的功率谱密度如图4所示，改进算法能够很好地抑制干扰信号，无需进行时间连续性检验。

图4 2012年1月4日00:10北京MST雷达东波束与西波束经改进算法处理后5个距离库高度功率谱密度(加粗曲线表示识别出的目标回波信号)

3 基础数据估算及算法有效性与可靠性检验

各阶矩参数计算方法主要有两种：一种是高斯拟合法(Gaussian fitting method)[41]，另一种为加权矩法(the weighted moment method)。根据Yamamoto等[42]与Wilson等[43]的研究，高SNR时加权矩法估算结果更好，低SNR时则相反。经改进算法处理后，目标信号具有高SNR，因此本文使用加权矩法。Woodman[44]给出了加权矩法的各阶矩计算公式。

根据MST雷达五波束探测方式，若假设观测区域内的水平风场均匀，则可以用多波束估算法进行三维风场计算。多波束估算法是将三波束估算法与五波束估算法进行联合使用的方法，何平[45]详细介绍了对相关计算方法。

应用改进算法处理得到的估算结果、雷达产品数据以及探空数据廓线如图5所示，改进算法估算的水平风速与风向与探空数据有很好的一致性，改进后算法估算的基础数据，连续性明显增强，异常值出现概率减小。由2012年1月1日—12月31日改进算法与雷达原算法得到的SNR、谱宽(各11593组对比廓线)对比(图6)可以看到，对于SNR，改进算法得到的结果更符合实际，即随高度增加SNR减小，直至为负数，而雷达原算法得到的结果全部为正值(图6a)。雷达原算法由于未精确识别目标回波，得到的谱宽明显偏大，改进算法得到的谱宽平均值为2.5 m·s-1，标准差也小于雷达原算法，所得谱宽更可信(图6b)。

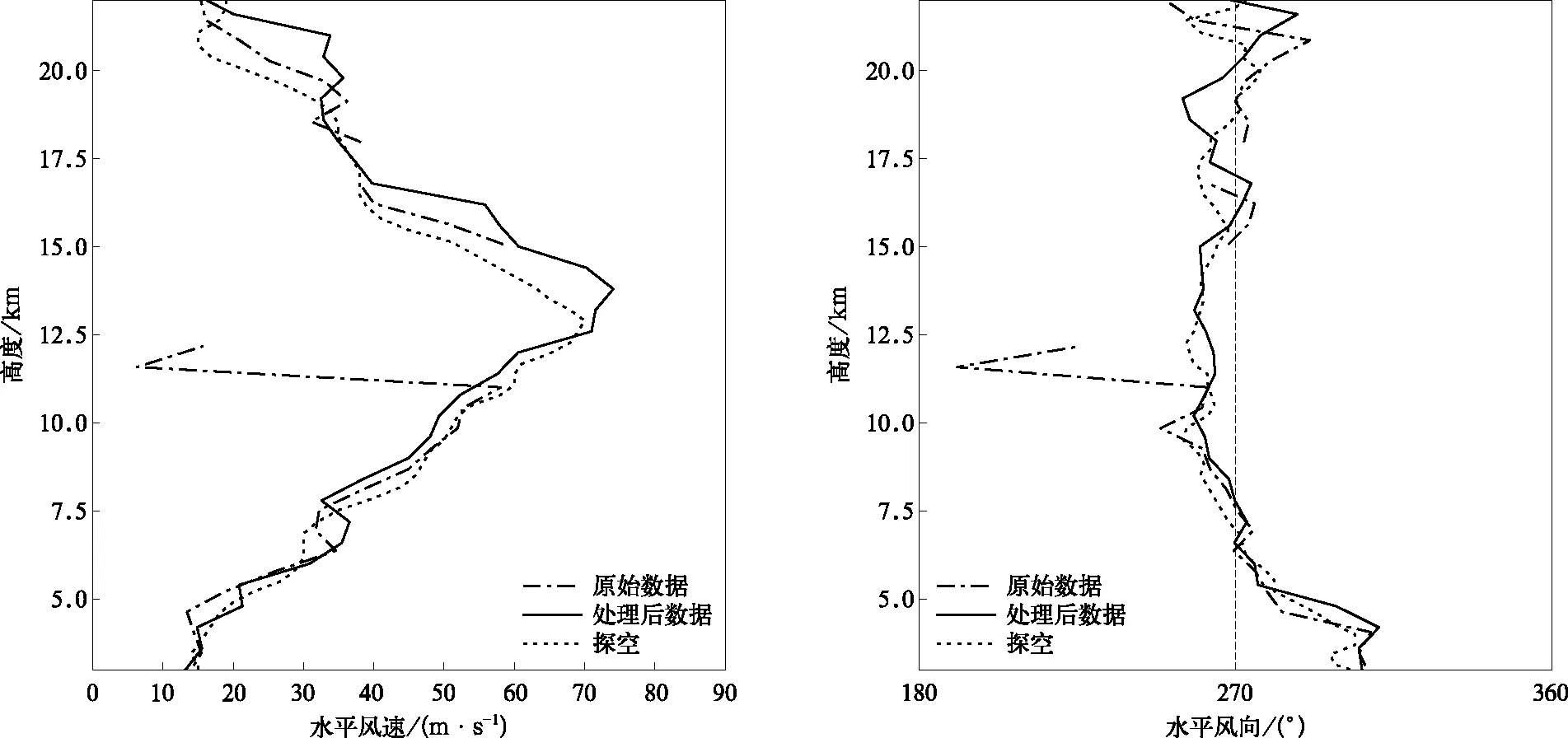
图5 2012年3月16日11：40北京MST雷达原算法与改进算法得到的水平风速、水平风向与探空(11:15)对比

图6 2012年1月1日—12月31日信噪比(a)和谱宽(b)的年平均值(曲线)和标准差(阴影)廓线

为进一步检验改进算法的有效性和可靠性，分别应用改进算法和雷达原算法得到2012年1月1日—12月31日的纬向风、经向风与垂直速度。纬向风和经向风同北京探空测值进行对比(共504组比对廓线，见图7)，垂直速度与ERA5再分析数据进行比对(共5312组对比廓线，见图8)。由图7可知，在3～22 km高度范围内，改进算法得到的纬向风与探空测值的平均差值在-1～0 m·s-1范围内，与雷达原算法相比更接近探空测值。由图8可知，在3～22 km高度范围内，改进算法得到的垂直速度与ERA5再分析数据的平均差值和差值的标准差分别在-0.05～0.05 m·s-1和0.25～0.3 m·s-1范围内，明显小于雷达原算法与ERA5数据的差异(平均差值和差值的标准差分别在-0.35～-0.25 m·s-1和0.4～0.5 m·s-1范围内)。改进算法得到的垂直速度与ERA5数据的差异明显小于雷达产品与ERA5数据的差异。

图7 2012年1月1日—12月31日北京MST雷达原算法与改进算法得到的经向风、纬向风与探空对比

图8 2012年1月1日—12月31日北京MST雷达原算法与改进算法得到的垂直速度与ERA5再分析数据对比

改进算法可更准确地识别大气湍流信号，有效抑制杂波及降水信号的干扰。为检验改进算法在降水天气条件下的有效性，将2012年共16组降水天气条件下(根据雷达站所在地历史天气记录全天有降水时段，7月25，26，28，31日，8月3日及12月13日，20日)的探空与北京MST雷达原算法及改进算法得到的经向风和纬向风廓线进行统计，结果如图9所示。由图9可知，降水条件下改进算法得到的经向风和纬向风与探空测值的平均偏差及均方根误差均小于雷达原算法与探空测值比对结果，验证了改进算法在降水天气条件下的有效性和可靠性。

图9 2012年16组降水天气条件下北京MST雷达原算法与改进算法得到的经向风、纬向风与探空测值平均差值和均方根误差廓线

综上所述，基于2012年多种数据对比分析，使用改进算法得到的经向风、纬向风与探空测值更接近，垂直速度、SNR及谱宽数据可靠性更高，同时改进算法在降水条件下依然有效。

4 结论与讨论

本文从噪声电平估算和目标回波准确识别与提取两方面对北京MST雷达功率谱处理算法进行改进，并验证算法的有效性与可靠性。改进算法可用于北京MST雷达历史观测数据，结果表明：

1)对数-线性拟合方案估算得到的噪声电平与二分法方案估算值一致，二者差值的标准差、平均绝对差值与相关系数分别是0.43 dB，0.21 dB和0.998，前者的平均值为168.6 dB，后者的平均值为168.5 dB。对数-线性拟合方案可快速、准确估算高斯白噪声的噪声电平值，利于后续目标回波信号的准确识别且业务实用性强。

2)对数-线性拟合方案具有两个明显优势：对数-线性拟合方案不需要预设参数，使算法更加简便；对数-线性拟合方案能够判断功率谱密度中能否提取出目标回波信号，是否需要进行后续数据处理步骤，提高计算速度与效率。

3)北京MST雷达使用改进算法后，非目标回波被有效抑制，目标回波可被准确识别与提取，可在功率谱密度图中更精确地显示大气湍流信号。

4)在3～22 km高度范围内，改进算法处理结果与探空纬向风均方根误差为2～3 m·s-1，而雷达产品与探空纬向风均方根误差为3～4 m·s-1。此外，改进算法得出的谱宽平均值为2.5 m·s-1，小于雷达产品平均值，改进算法得到的垂直速度与ERA5数据差异明显小于雷达产品与ERA5数据的差异。

5)在降水天气条件下，改进算法处理结果和探空测值在不同高度的水平风速平均偏差和均方根误差均小于雷达产品和探空差值。

从本文分析可知，改进算法有效可靠，明显改善雷达数据质量且易于实现。该算法的原理与实现方法具有普适性，可用于有相同探测机制的各类MST雷达、ST雷达和风廓线雷达的数据处理，但算法的有效性与可靠性需进一步检验。本文是基于信号处理方式固定条件下改进了数据处理算法，若将信号处理与数据处理的改进相结合，则可更有效地提高雷达数据质量。

致 谢:本文使用了国家重大科技基础设施“子午工程”科学数据。感谢中国科学院大气物理研究所香河大气综合观测试验站工作人员对MST雷达运维所做的工作。