几个特殊广义积分的计算
2020-10-28 02:00丛爱玲韩朝阳
牡丹江教育学院学报 2020年9期
丛爱玲 韩朝阳
(1牡丹江市教育教学研究院, 黑龙江 牡丹江 157000;2哈尔滨理工大学理学院, 哈尔滨 150080)
对于一些积分计算题我们很难采用常规方法得出原函数,甚至根本不能用初等函数来进行表示,利用几个特殊广义积分的计算结果作为结论处理这些计算题,很容易处理复杂的积分计算。
1 Euler积分
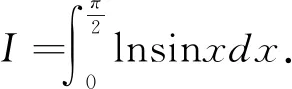
解:这是一个无界的瑕积分,瑕点为x=0.利用柯西判别法,容易验证该积分的收敛性。
先做代换x=2t,得到
所以答案为
2 Froullani积分
设函数f(x)在[0,+)上连续,极限f(+)存在且有限,实数a,b>0,计算积分
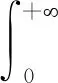
解 本题广义积分的收敛性将在下面的计算过程中建立。对0 对上式右边的两个定积分分别应用积分第一中值定理,得到 在上式中分别令r→0+,R→+,注意到这时ξ→0+,η→+,由于f(0+)=f(0),f(+)存在有限,而且在此时的极限为Froullani积分,得到 除此之外,从上面的证明过程中可以得到Froullani积分的两种变型: 若x→+时f(x)没有有限极限,但是对某个A>0,积分收敛,则有 因此Dn(x)在[0,π]上可积。直接对Dn(x)积分比较困难,为此我们利用三角恒等式作如下变换 将Dn(x)分解为 逐项积分得到 现在再来证明Dirichlet积分,先观察将其分母换为x所产生的影响。因为 可见有 因此f(x)在[0,π]上常义可积。应用Riemann引理就有 得到 即证得 4Euler-Possion积分 证明:由于积分值只与被积函数和积分区域有关,与积分变量无关,从而我们有 用极坐标变换x=rcosθ,y=rsinθ转化为二重积分进行计算,则有 因为e-r2≥0,则I≥0,即 得证。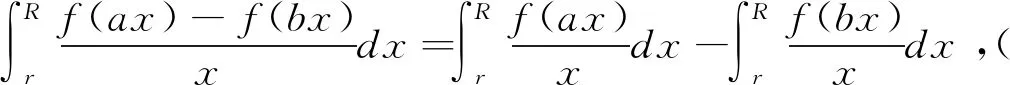
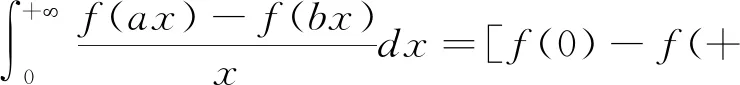
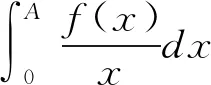
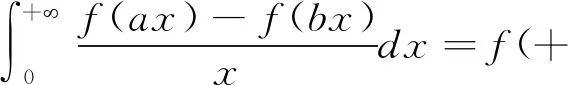
3 Dirichlet积分
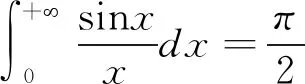
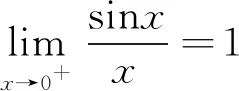
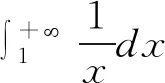
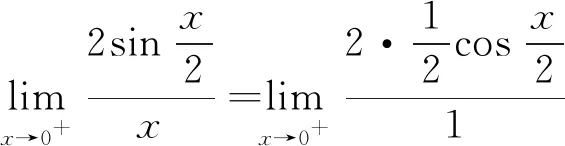
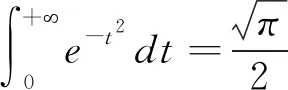


猜你喜欢
车主之友(2022年6期)2023-01-30
数学年刊A辑(中文版)(2021年3期)2021-11-05
上海建材(2020年5期)2020-12-15
小学生学习指导(低年级)(2020年11期)2020-12-14
数学物理学报(2020年3期)2020-07-27
中学生数理化(高中版.高考数学)(2020年2期)2020-04-21
数学物理学报(2019年5期)2019-11-29
中学生数理化(高中版.高考理化)(2019年3期)2019-04-25
大学生(2017年7期)2017-07-17

