长河坝特高土石坝爆炸动力响应分析

胡良明，杨 涛，张志飞，欧阳儒贤

(1.郑州大学 水利科学与工程学院，河南 郑州 450000； 2.中国能源建设 浙江省电力设计有限公司，浙江 杭州 310000)

近年来，由于水资源的分配需求，我国西部建设了一批特高土石坝，如两江口土石坝、古水土石坝等。由于特高土石坝属于高坝大库，一旦溃坝，可能导致梯级水库的接连溃坝[1-3]，造成难以想象的后果。

对于爆炸荷载作用下大坝的动力响应分析，国内外学者做了一定的研究。刘晓蓬等[4]采用LS-DYNA软件，研究了RHT本构模型在爆炸荷载反应中应用的可行性，得出泡沫混凝土能有效降低大坝的爆炸损伤。薛新华等[5]分析了爆炸荷载作用下拱坝的破坏与损伤情况，得出爆炸时的拱坝的应力集中部位和爆炸冲击荷载主要作用方向。李鸿波等[6]采用三维动力模型，模拟分析混凝土重力坝及岩石基础在爆炸冲击荷载作用下的应力场、位移场、应变、损伤场、破坏失效分布场和能量释放率等动力响应。张社荣等[7]构建爆炸全耦合模型，研究了重力坝破坏模式与水下炸弹起爆时的水下深度、炸药量等的关系。Afriyie等[8]在考虑不同水库水位和不同土壤密度的情况下，研究了爆炸对大坝产生的爆坑尺寸大小。

到目前为止，对特高土石坝在爆炸荷载作用下的破坏研究较少。本文针对长河坝特高土石坝在爆炸荷载作用下的应力及位移等因素进行研究，对同类工程设计及安全运行具有参考价值。

1 模型建立与参数选取

1.1 模型建立

长河坝水电站位于四川省甘孜藏族自治州康定县内[9]，大坝为砾石土心墙堆石坝。坝高最高为240 m，坝顶长为497.94 m，坝顶宽为16.00 m，上游和下游的坝坡均为1∶2.0。心墙底高程为1 457.00 m，最大底宽为125.75 m。坝体计算模型采用整体直角坐标系，X轴以顺水流方向为正，Y轴以左岸指向右岸为正，Z轴以竖直向下为正。共剖分的单元数为821 195个，节点为1 630 908个。模型网格如图1所示，为节省篇幅，模型验证见文献[10]。

图1 模型网格Fig.1 Model mesh

1.2 参数选取

弹塑性材料模型采用DL/T 5395-2007《碾压式土石坝设计规范》[11]中的模型，屈服条件采用Krieg提出的偏量塑性屈服函数，具体见式(1)～(2)[12]。

h=J2-(a0p2+a1p+a2)

(1)

J2=SijSij/2

(2)

式中：p为压力；J2为应力偏张量的第二不变量；Sij为应力偏量张量；a0，a1，a2为屈服函数参数，a0，a1参照文献[13]取值为0；其他参数坝体密度ρ、泊松比υ、a2、弹性模量E和剪切模量G的取值如表1所列，具体参数选取见文献[14-16]。

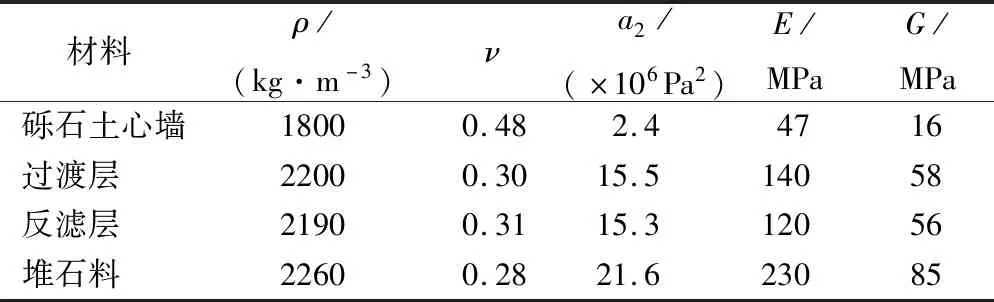
表1 砾石土心墙、堆石料、反滤层、过渡层参数Tab.1 Parameters of gravelly soil corewall, rockfill material, inverted filter, transition layer

2 状态函数与爆炸荷载

2.1 炸药状态函数

针对炸药爆炸后的爆炸产物，本文采用JWL状态方程用以描述爆炸产物的膨胀做功过程，JWL状态方程形式见式(3)。

p=A1(1-ω/R1V)eR1V+A2(1-ω/R2V)eR2V+ωE/V

(3)

式中：p为爆炸时内部的压力；V为爆炸后产物的体积；E为单位体积爆炸产物的内能；A1、A2、R1、R2和ω为常数。TNT炸药关于JWL的相关参数如表2所列。

表2 TNT炸药关于JWL方程参数Tab.2 JWL equation of state parameters of TNT explosives

2.2 空气状态函数

空气方程采用Linear-Polynomial理想气体状态方程,见式(4)。

P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E

(4)

(5)

式中：C0～C6为气体状态方程系数，常数；E为初始能量系数；μ为比例体积，空气的状态方程参数如表3所列。

表3 空气状态方程参数Tab.3 Equation of state parameters of air

2.3 爆炸荷载

本次模拟炸弹从坝前射入大坝，采用200 t TNT炸药[17]作为荷载源。为了便于观察，将坝体从中轴线切开，在中轴线处施加对称约束，即实际荷载为100 t TNT炸药。爆炸时间参考常规武器地面爆炸动荷载的爆炸特性及美军TM5-585-1手册[18]，设置为0.05 s。起爆点参考文献[19]选取，坐标为(-188,0,105)(单位：m)。起爆点细部网格图和切线位置俯视图如图2和图3所示。

图2 起爆点细部网格Fig.2 Detonation point detail mesh

图3 切线位置俯视图Fig.3 Tangential position top view

3 计算结果分析

3.1 应力分析

重点分析爆炸后特高土石坝应力变化情况。因篇幅限制，仅给出爆炸荷载结束时刻，即t=100 ms时，沿坝体X方向应力云图如图4所示。爆炸区域附近以压应力为主，主要出现在炸点周围偏向坝体一侧，最大压应力为43.3 MPa。炸点外部区域出现拉应力，最大值为49.5 MPa，远超过岩土散粒体的强度。

图4 坝体在100 ms时的X方向应力(单位：kPa)Fig.4 X direction stress of dam at 100ms

3.2 破坏区长度与深度分析

重点分析爆炸后坝体内部的破坏区大小，因篇幅限制，仅给出爆炸荷载结束时刻，即t=100 ms时，水平方向和垂直方向的坝体破坏区长度如图5所示。此时，水平方向坝体被压实，爆炸面达到最大值，水平方向最大破坏区长度为14.22 m。由于垂直方向坝体较薄，爆炸在垂直方向较水平方向冲击大，垂直方向破坏区深度最大为29.96 m，破坏区域在平面上呈近椭圆形。

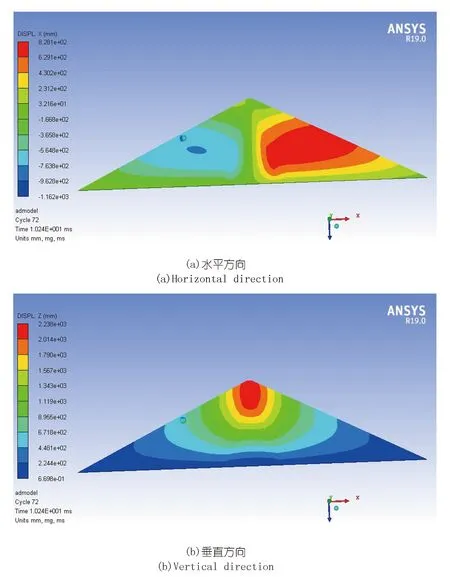
图5 坝体在100 ms时水平和垂直方向位移及爆坑尺寸(单位：mm)Fig.5 Damage zone length of the dam at 100ms in horizontal and vertical direction

3.3 对坝体内部应力的影响

为了进一步分析坝体内部在爆炸荷载作用下的应力分布特征，选取10个观测点进行应力分析：监测点1～7布置于心墙中心处，间距为40 m；监测点8～10布置在爆炸中心的水平方向，每隔10 m沿X方向往坝体内布置。监测点布置如图6所示。

图6 监测点布置Fig.6 Layout of monitoring points

如图7所示：靠近爆炸附近的应力衰减较快，观测点8的X方向压应力最大值为60.0 MPa；测点10的X方向压应力最大值为22.0 MPa。表明仅相距20 m，X方向最大正应力下降幅度为63.33%。可以预见离炸药更远处的坝体受到的影响会更小。由图7还可看出：心墙处会由于爆炸产生的冲击而产生压应力和拉应力，最大压应力发生在心墙底部的观测点7，为3.1 MPa；坝体内部观测点5的拉应力最大，为5.2 MPa。

图7 监测点的X方向应力Fig.7 X direction stress of monitoring points

4 结 论

(1) 爆炸发生后，坝体主要以压应力为主，炸点附近局部会出现应力集中现象，往外的区域变为拉应力，拉应力最大值可达49.5 MPa，发生在坝体表面。

(2) 爆炸荷载冲击下，破坏区域大小随时间呈正相关，水平方向破坏区长度最大为14.22 m，垂直方向破坏区深度最大为29.96 m，破坏区域平面上呈近椭圆形。

(3) 土石坝发生爆炸后，由于内部坝体被压实，对炸点附近区域影响较大，对远处坝体影响较小。当冲击波传递到心墙处时，心墙中下部拉应力增大，最大可达5.2 MPa，心墙底部压应力增大，最大可达3.1 MPa，由于心墙是土石坝最重要的防渗部位，在设计时应引起足够的重视。