泄流雨雾条件下岩质边坡稳定性的耦合分析

程光威,路 颜,张 媛,周 奎

(1.陕西铁路工程职业技术学院轨道工程系,陕西 渭南 714000; 2.机械工业勘察设计研究院有限公司,陕西 西安 710000)

通过查阅大量工程研究资料可知,对于水电站泄水边坡,当泄流雨雾慢慢渗入到岩体中,就会使边坡处于非饱和区的水头压力在短时间内迅速升高,从而产生暂态饱和区[1],该区域的水压力会在短时间内保持稳定,边坡的稳定性明显降低[2]。具体原因在于,雨雾渗入到岩体中,就会形成一部分附加的水荷载[3],在比较短的时间内,岩体自身的质量增加,下滑力得到了很大的提升,同时由于渗流场的变化[4],岩体的摩阻系数降低,故而增大了滑动风险。对于岩质边坡裂隙发育的区域,泄流雨雾一旦渗入,就会产生更加严重的影响。

近年来,对于暂态水压力的增加均处于定性研究阶段,截至目前,定量研究的成果少之又少,很多工程设计都是假定参数来进行计算。比如,在漫湾水电站工程中,采用静水压力乘以0.4的方法进行计算;在三峡工程中,采用静水压力乘以0.4的方法进行计算,也就是折减系数假设为0.3。从以上数据可以看出,采用不同的方式进行边坡暂态水压力计算时,所产生的结果差异很大,而且,这些方法都是专家学者依据经验假设的数据。

为了更好地对岩质边坡饱和-非饱和渗流现象进行深入研究[5],此处以达西定律为基础[6],推导出饱和-非饱和状态的渗流方程,并建立Hoek-Brown准则[7]下的边坡岩体安全系数公式。同时,选择某水电站具有代表性的剖面作为研究对象,完成数值模拟,分析泄流雨雾会对施工工程中的边坡渗流场和稳定系数产生哪些影响,以期对施工工程中边坡安全性的评估、控制以及采用何种防治策略提供可靠的依据。

1 计算理论推导

1.1 基本方程

将质量守恒定律与渗流的微积分方程进行结合[8],进而推导出边坡处于饱和-非饱和状态时的边界渗流方程。当边坡处于非饱和的状态时,边坡岩体的渗流满足达西定律。此方程中,将压力水头作为1个未知量,在二维状态下,饱和-非饱和状态下的渗流基本方程可以表示为

(1)

其中:kr表示相对渗透率;kij表示饱和渗透张量;h表示压力水头;x2表示正向向上的垂直坐标;C表示比容水度;β表示系数,当系统处于非饱和区时,β=0,当系统处于饱和区时,β=1;Ss表示单位贮存量;t表示时间;S表示源汇项。

在式(1)中所指的定解条件主要是初始条件以及边界条件。

初始条件主要由压力水头决定:

h(xi,0)=h0(xi),i=1,2

(2)

其中:h0的值是由xi的值所决定的。

压力水头的边界条件可以表示为

h(xi,t)=hc(xi,t),i=1,2

(3)

其中:hc的值是由xi以及时间t2个参数共同决定的。

已知渗流流量边界可以表示为

(4)

其中:ni表示边界垂直方向矢量中的第i个分量;v的值是由xi以及时间t2个参数共同决定的。

1.2 Hoek-Brown准则下的安全系数方程

在Hoek-Brown准则下,岩质边坡的粘聚力和内摩擦角分别为

(5)

(6)

考虑饱和-非饱和效应时,抗剪强度为

τf=c+(σ-μa)tanφ+(μa-μw)tanφb,

(7)

其中:σ表示应力插值;μa表示空隙气压力;μw表示空隙水压力;φb表示提高的粘聚力值。

由公式(5)～(7)可得

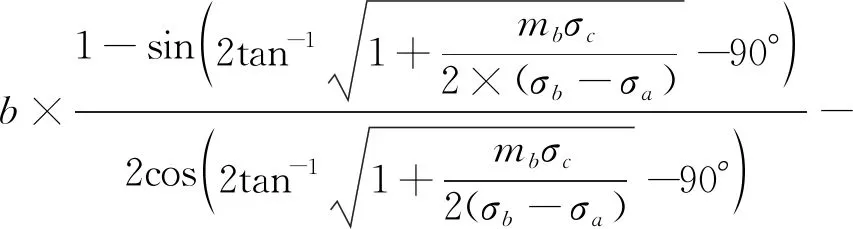
μatanφb+σtanφ=c′+σtanφ。

(8)

此时粘聚力为

μatanφb。

(9)

结合Bishop理论[9],考虑饱和-非饱和效应下Hoek-Brown准则,代入强度参数可得边坡安全系数Fs:

(10)

2 计算模型及参数

2.1 计算模型

该边坡地层按岩性划分,主要包括三叠系中统板岩、板岩夹砂岩和局部花岗岩,边坡表面主要被第四系薄层坡积块碎石土所覆盖。有限元模型可简化为4种材料,分别是第四系覆盖层、松动变形体、弱风化岩体、 微风化岩体,故建立有限元计算模型如图1(a)所示,加载地下水边界条件的渗流模型如图1(b)所示。

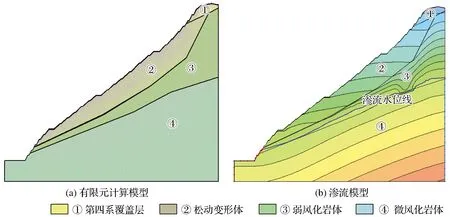
图1 有限元计算模型及渗流模型Fig.1 Finite element calculation network model and seepage model

边坡的初始条件为:当黄河水位到达2 755 m时边坡剖面的地下水位值。边界条件:后缘部分山体的截面水位达到2 975 m时的边界值;泄水区域边坡的坡面超过2 755 m时,上面的区域被认为是雨雾入渗;坡面高度低于2 755 m时下面的区域是出逸边界。

由于不同高程泄流雨雾强度不同,随着高程增加雨雾强度减弱,按照高程可分为4个不同的雨雾区域(见表1)。

表1 雨雾强度区域划分

2.2 计算参数

由室内试验结合经验取值,各种材料的基本参数如表2所列。

表2 各类介质物理力学参数Table 2 Physical and mechanical parameters of various medias

边坡岩体各类介质的渗透系数如表3所列。

表3 各类介质渗透系数

3 计算结果

3.1 渗流规律

泄流雨雾保持1 d、10 d、15 d、30 d 4种不同的情况下出现的压力水头等值线数值如图2所示。分析图2可知当泄流雨雾的保持时间慢慢增加时,第四系覆盖层和松动变形体内部区域的压力水头值也在逐渐增加,而且在某些特定区域产生了暂态饱和区域;边坡内部区域的地下水位线也在慢慢升高。

图2 4种工况下的水头等值线Fig.2 Head contour maps under four working conditions

从图2中还能够看出,坡体表面覆盖层渗透系数值比较大,泄流雨雾持续的时间会对压力水头的分布产生很大的影响。对于松动变形体而言,其边坡岩石风化的现象比较明显,而且产生了比较多的节理裂缝,这种情况下泄流雨雾更容易入渗。随着渗流时间的不断延长,该区域的压力水头参数值变化较大,在坡体比较浅的区域经常会产生暂态饱和区,并且暂态饱和区面积也会慢慢增加,达到一定数量后趋于稳定。当泄流雨雾逐渐停止之后,这些饱和区会慢慢向下移动,最终全部消失。

3.2 不同工况下的位移

泄流雨雾保持1 d、10 d、15 d、30 d 4种不同的情况下出现的压力水头等值线参数值如图3所示。分析图3可知当泄流雨雾渗流持续1 d之后,边坡内部的区域就会产生缓慢的变形,其变形的范围为0.02～0.3 mm;当泄流雨雾渗流持续10 d之后,边坡内部变形的区域逐渐增大,其变形的范围为0.08～0.9 mm;当泄流雨雾渗流持续15 d之后,边坡内部的区域变形的范围增大至0.2～1.3 mm;当泄流雨雾渗流持续30 d之后,边坡内部的区域变形的范围将会达到0.8～1.7 mm。

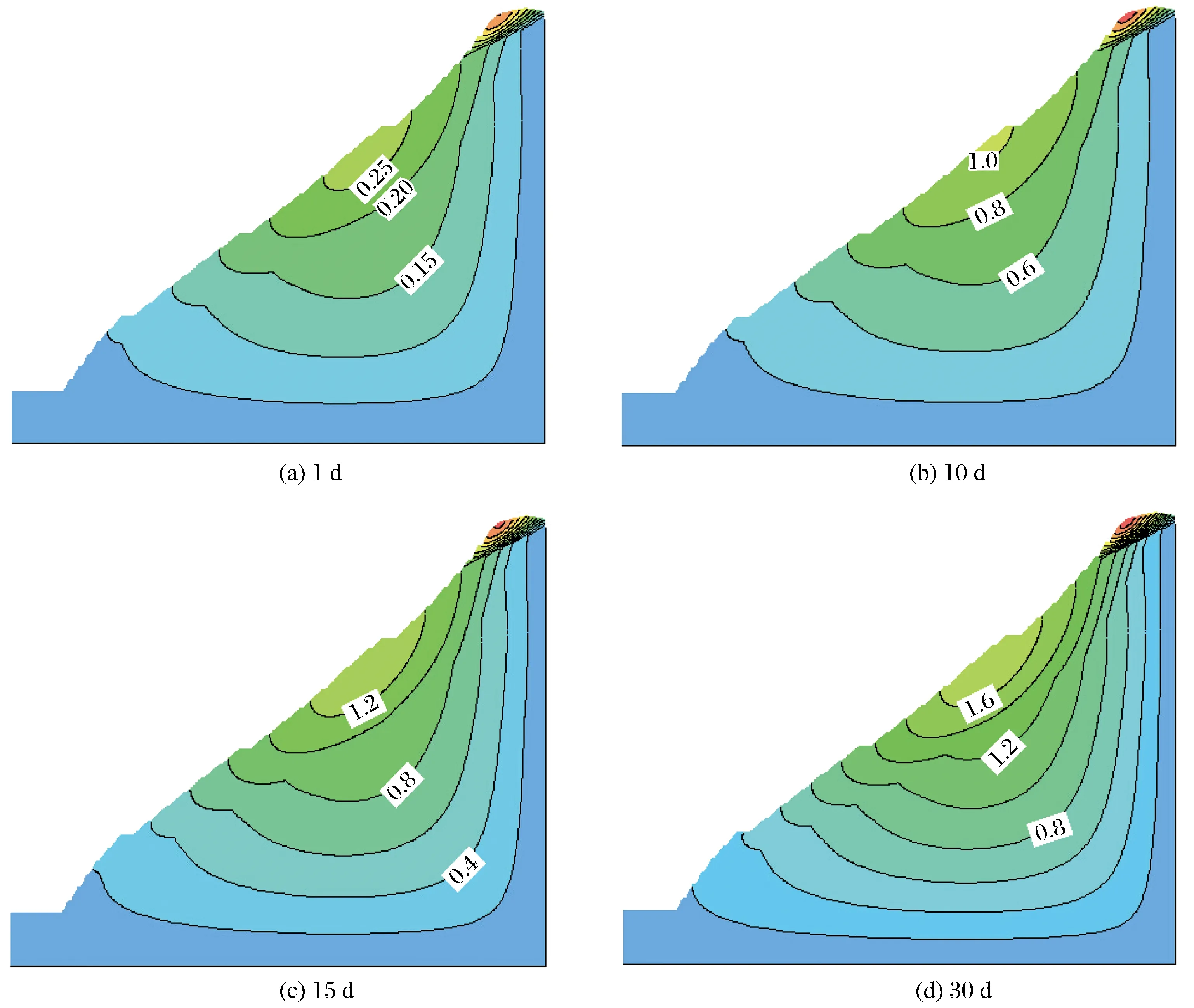
图3 4种工况下的位移等值线Fig.3 Displacement contour cloud map under four working conditions

由此可知,当雨雾渗流持续的时间逐渐增加时,水就会顺着某些比较软弱的结构区域,例如节理裂隙,慢慢渗入到边坡岩体内部的区域,使边坡内部区域的位移场发生改变,坡体部分区域的位移值逐渐增大,其中增大值比较明显的区域是坡体上部的第四系覆盖层和松动变形体。因为这2个区域的岩体发育有较多的节理裂隙,其渗透系数明显高于其他区域,故而更容易入渗,所以当渗流时间逐渐增加时,其位移值也会变化较大,这种情况会对边坡稳定造成很大的影响。

通过有限元计算边坡在不同雨雾工况时的稳定性系数,边坡稳定性系数随雨雾时间的变化如图4所示。由图4可以看出,随着雨雾渗流的时间不断延长,边坡稳定性系数呈现逐渐减小的趋势,并且这种降低幅度在慢慢减小。出现这种现象的原因在于,渗流逐渐增加,坡体部分区域出现暂态饱和,进而产生超静孔隙水压力,降低坡体安全系数;随着渗流时间逐渐增加,坡体产生暂态饱和区的数量就会越来越多,但是当暂态饱和区的数量超过某一特定的数值时,其数量就不会再次增多,此时,坡体安全系数就会逐渐趋于稳定,安全系数曲线逐渐趋于平缓的状态。

图4 边坡稳定性系数随雨雾时间变化情况Fig.4 Variation of slope stability coefficient with flood and fog discharge

4 结论

在达西定律的基础上,将质量守恒定律和渗流偏微分方程相结合,从而推导出了饱和-非饱和状态下的边界渗流方程。基于Hoek-Brown准则,得出饱和-非饱和状态下边坡岩体的安全系数公式,并以某水电站泄水边坡为工程实例建立了渗流场与应力场耦合的等效连续介质模型,进行耦合计算,得出了泄流雨雾持续不同时间下的边坡渗流水头等值线、位移等值线以及安全系数。通过分析计算结果可知,坡体表面及上部存在较多节理裂隙的区域,在雨雾渗流影响下,渗流场和位移场会发生较大变化,同时伴随大量暂态饱和区出现,且随着雨雾时间增加而增加,导致坡体安全系数降低。但是,暂态饱和区的面积达到一

定值时几乎不再变化,此时边坡安全系数逐渐趋于稳定且大于1,可认为该边坡基本稳定。但考虑到此时坡体安全系数为1.5,仍然较小,故需采取相应的稳定边坡措施,建议适当削坡减载。