一种新的二进小波滤波器的构造及应用研究

何 笑,王 刚,卢维娜

(新疆师范大学数学科学学院,新疆 乌鲁木齐 830017)

小波分析[1]具有良好的局部化能力和多分辨率分析能力,它是在Fourier分析的基础上发展而来的一种新的时频分析工具。同时其具有提供时间和频率分析能力,也是信号处理中的有力工具[1-6]。已知利用滤波可以从复杂的信号中提取所需要的信息,而滤波器同样具备一些重要的性质[7-9]。但是同时具有正交性、紧支撑和对称性这些性质的小波只有Haar小波[1-10]。与双正交提升方案相同,二进提升方案[1]使小波分析的应用领域得到了拓展,其可根据实际需求构造不同的二进小波或双正交小波。研究从消失矩的条件出发,根据该方案提出了一种新的提升二进小波滤波器的构造方法,并且将所构造的滤波器应用于图像增强中。实验表明图像的信息熵、清晰度以及峰值信噪比都有了明显提高,对图像质量的改善有了一定的帮助,提高了图像的利用价值。

1 二进提升方案

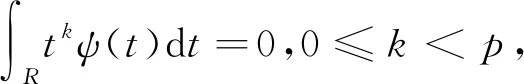
(1)

(2)

2 B-样条二进小波的构造

所提方法是Mallat提出的构造方法[1]的推广,m次B-样条函数φ(t)是特征函数χ[0,1](t)与其自身的m+1次卷积的平移,即

φ(t)=χ*χ*…*χ[0,1](t),

(3)

其傅里叶变换为

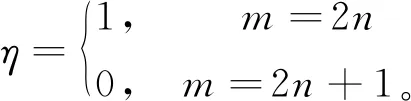
那么,由二尺度关系可得

(4)

(5)

由式(2)可得

(6)

所以由式(1)可得

(7)

尺度函数φ(t)与小波函数ψ(t)在r=2,m=3时的B-样条二进小波滤波器的系数见表1。初始尺度函数φ(t)与小波ψ(t)的图形见图1。

表1 r=2,m=3时的B-样条初始二进小波滤波器的系数

图1 初始尺度函数φ(t)与小波ψ(t)的图形Fig.1 Graph of initial scaling function φ(t) and wavelet ψ(t)

3 二进提升小波的构造

3.1 构造定理

根据文献[1]中提出的二进提升方案,调整方案中自有参数的形式,可以构造满足某种特性的B-样条二进小波滤波器。

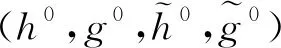
(8)

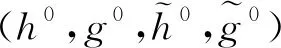
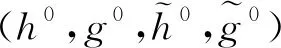
(9)

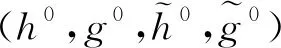
(2) 若二进小波分解高通滤波器g0有p阶消失矩,则提升后的二进小波分解高通滤波器g有至少p+1阶消失矩的充分条件是

反复应用该定理,q(q>p)阶消失矩的二进分解高通滤波器可以被构造出。

3.2 提升二进小波的构造

以r=2,m=3构造的新的B-样条二进小波滤波器作为初始滤波器,利用定理1可得到具有更高阶消失矩的提升二进小波。

表2 一次提升二进小波滤波器的系数

图2 一次提升后的对应的2个尺度函数和小波的图形Fig.2 The corresponding two scale functions and wavelet after improvement once

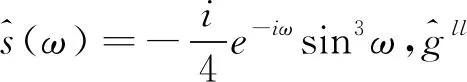
同样,继续应用此定理可得到具有更高阶消失矩的二进小波滤波器。从表1～表3可以得出,所构造的提升二进小波滤波器的消失矩的阶数有了明显的提高。

表3 二次提升二进小波滤波器的系数

图3 二次提升后的对应的2个尺度函数和小波的图形Fig.3 The corresponding two scale functions and wavelet after improvement twice

4 算法实现

4.1 低频系数增强处理

经二进小波变换后产生的低频子带会对原图的对比度造成很大的影响,使用单尺度Retinex算法[11-12]改善图像亮度分布均匀性,提高图像的整体对比度,基本思路是:构造高斯环绕函数,然后利用高斯环绕函数对图像的3个色彩通道分别进行滤波,滤波后的图像就是估计的光照分量,接着在对数域中对原始图像和光照分量进行相减得到反射分量作为输出结果图像,其具体的表达式为

log(fi(x,y))-log(fi(x,y)*G(x,y)),

(10)

其中:f(x,y)为原始图像;R(x,y)为反射分量;L(x,y)为光照分量;ri(x,y)表示第i个色彩通道的反射图像;*代表卷积;G(x,y)为高斯环绕函数,G(x,y)的构造为

(11)

其中:σ为高斯环绕的尺度函数。

4.2 高频系数降噪处理

在二进小波域中,高频部分中的许多重要信息被噪声淹没,需使用能降低高频成分幅度的滤波器减弱噪声的影响,从而获得有用的信息。研究选择中值滤波[12]来处理高频部分的噪声,即在每一幅高频图像中取9个像素点,即3×3的矩阵,将9个像素值进行排序,最后将这个矩阵的中心点赋值为这9个像素的中值,如图4所示。

5 实验过程

为了验证所构造的滤波器在图像增强中的应用效果,选取实验平台为MATLAB R2016a,实验对象是2组大小为256*256,jpg格式的浑浊水域中的彩色水下图片。

5.1 实验步骤

(1) 对彩色图像的3个通道分别进行二进小波变换一层分解,分别选取表1～表3的数据作为分解与重构滤波器;

(2) 利用式(10),对分解后的低频图像进行处理,实验表明σ=80效果好;

(3)对分解后的高频部分分别使用掩模大小为5×5的中值滤波消噪处理;

(4) 再次选取表1～表3的数据作为重构滤波器,对处理后的高频与低频部分进行二进小波逆变换;

(5) 最后对重构的3个通道进行灰度拉伸再融合,得到目标图像。

5.2 实验分析

2组实验的结果分别如图5、图6所示。观察原始图像可以发现,水体很浑浊,噪声很大,图像的细节信息非常模糊,颜色失真情况很严重,存在严重的偏绿、偏蓝色调现象,不利于人眼观测,从而很难获取有用的信息,使得图像的利用价值很低。而使用新构造的滤波器对原始图像进行分解与重构,在第1组实验中,图5(b)中最大的变化就是偏绿色调已经不存在,图像中的水体变得清晰了,鱼群和鱼身上的颜色条纹可以清晰可见;图5(c)中除了偏绿色调消失、鱼和鱼身上的颜色条纹清晰可见外,相比图5(b),鱼群的背景有了一定的提亮;图5(d)包含了图5(b)和5(c)中所有的优点,另外,图5(d)中右上角部分亮度比图5(b)和5(c)中的亮度有所提高。在第2组实验中,如图6(b)所示,图像中的水体变得清晰了,偏蓝色调不存在,鱼的轮廓边缘,尤其是鱼嘴部分,清晰可辨,鱼身上的颜色条纹非常清晰,局部过亮和光晕现象也没有发生;图6(c)中除图6(b)所包含的信息,其右上角部分更加清晰;同样,图6(d)中除图6(b)和图6(c)所包含的信息外,图中的海藻背景更加明亮。从图5、图6可知,所构造的滤波器处理的图像其共同点就是偏蓝、偏绿色调现象不在出现,水体变得清晰,鱼的轮廓与鱼身上的颜色条纹清晰可见,背景里的海藻颜色和背景都有了一定的提亮,可见所构造的滤波器丰富了图像的信息,凸显了图像的细节信息,改善了图像的颜色失真情况,减少了噪声对图像质量的影响,非常利于人眼观测。

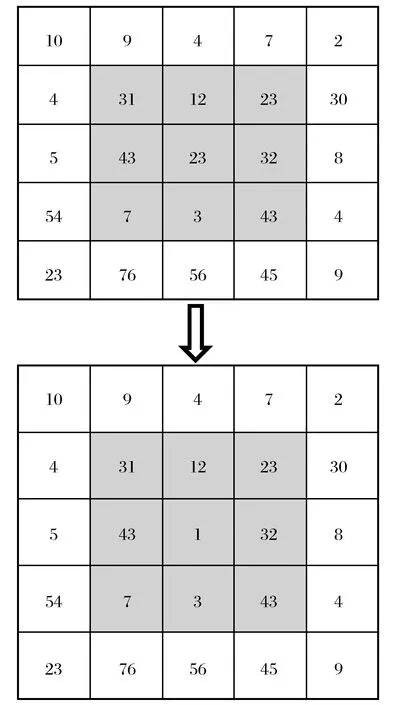
图4 中值滤波原理Fig.4 Schematic diagram of median filtering

图5 第1组实验结果Fig.5 The first set of experimental results

图6 第2组实验结果Fig.6 The second set of experimental results

为进一步说明构造的滤波器的有效性,同时避免主观分析带来的经验主义,选取图像的信息熵、清晰度和峰值信噪比作为客观评价标准(见表4)。

表4 增强方法的客观评价标准

6 结语

研究利用消失矩条件,对构造定理进行应用,构造了提升二进小波滤波器。根据表4中的数据可知,所提升的滤波器处理的图像在信息熵、清晰度以及峰值信噪比方面有了明显的提高,说明图像的质量有了一定的改善,图像的利用价值也有了一定的提高,说明该滤波器可适于图像增强方面,但是观察第1组实验结果可以发现,提升后的滤波器处理的图像,其边缘存在模糊现象,对人的视觉观测有一定的影响,可见所构造的滤波器在图像增强方面还是存在问题,因此在实际应用中还需进一步的研究。