基于 C-SVM 分类器对影响乘客选择出行方式的模型建立与求解
杨佳凝
(江苏大学,江苏 镇江 212013)
1 购票行为分析
本文根据 2019 年某高校本科生寒假回程购票信息调查表所给出的 161 组学生购票情况数据和因素调查、该高校本科生另一组回程信息调查表所给出的 85 组购票因素调查,筛选影响购票结果的主要因素,建立购票结果与影响因素之间的数学模型,对影响因素与影响因素之间的关系进行量化分析,从高到低排序,并预测下一年寒假每个学生的购票行为[1]。模型流程如图1所示。
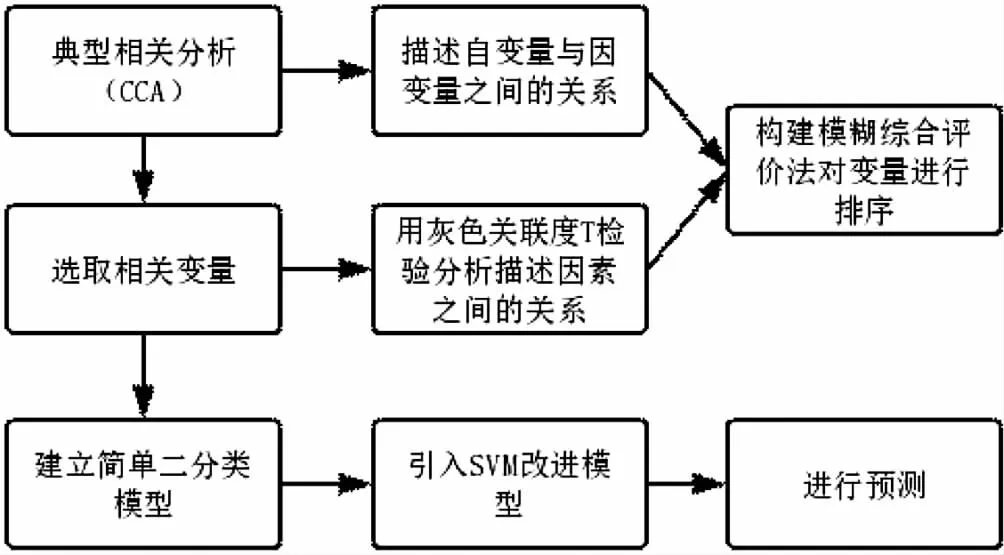
图1 模型流程
其次,考虑逻辑数据的分布情况。由于逻辑数据只有 0 和 1 两种状态,故检验其是否呈伯努利分布。令Fn等于伯努利分布函数,进行Kolmogorov-Smirnovtest,发现所有逻辑数据均不成伯努利分布[2]。
2 购买火车票和高铁票的主要因素
筛选购买火车票和购买高铁票的主要因素,并建立典型相关分析模型,先建立多元线性回归模型:
ym=β0+β1X1+β2X2+β3X3+β4X4β5X5β6X6+β7X7+β8X8
典型相关分析函数的因变量为人们选择购买高铁票还是普通火车票,自变量分别为影响人们出行的各个因素,即里程长度X1、时间X2、被迫选择X3、可支配收入X4、购票方式X5、购票价格X6、舒适程度X7以及时间成本X8。
其中,β0表示多元回归统计常数,β1,……,β8分别代表各个因素的权重。
由表1可知,系数越大,该自变量对因变量的影响程度越大,将这些系数所占的权重从高到低排序可知影响乘客购票行为的主要因素,其中,最主要的因素为两种交通工具的舒适程度,所占权重为0.046 6;次要因素为购票方式(自付或家庭报销),所占权重为0.045 5;排在第3位的因素为行驶时间长度,所占权重为0.036 8。
对于典型相关分析模型(CCA)进行显著性检验,记H(0)=0,表示原假设结果为真。经检验得知,显著性误差检验结果为 46 个,占比为 25%,在误差允许范围之内[3]。

表1 典型相关分析模型系数
将数据经过标准化处理后,运用sgn分类函数,经过 CCA 分析可以得到乘客购票行为(购买火车票还是高铁票)对各个自变量影响程度的大小,筛选出影响乘客购买高铁票还是火车票的主要因素,在对主要因素进行多元线性回归后,利用 sgn 函数进行二分类。为进一步刻画出乘客购买火车票还是购买高铁票的特征,需要对结果进一步分析,建立数学模型,将每位学生的特征标签化,将不同的标签赋予权重后,对学生购买火车票还是高铁票的行为进行分类,建立数学模型函数表达式为:y=sgn(βX)。
通过sgn符号函数分类,可将在[-1,0]上的数全部映射成-1(乘客购买火车票),将[0,1]上的数全部映射成1(乘客购买高铁票)。由此建立出影响乘客购票行为因素的准则并通过回归分析验证该模型的准确性。
3 因素与因素之间的量化行为分析
进一步量化分析因素与因素之间的关系,建立一个简单的二分类模型,用最小二乘法拟合其参数。但是验证后发现,拟合的准确率较低,为 84.47%。故而,需要优化二分类函数的线性部分,提高其准确率。本团队通过时间的角度加以分析。最后,建立模糊综合评价法,对影响乘客购票行为的因素从高到低进行排序。
那么,只需求出min‖Y-Y′‖2,即min‖Aβ-Y‖2。考虑到Aβ-Y是正规方程,用最小二乘法即可得出全局最优解,即β=(ATA)-1ATY,因此,得到简单二分类模型:
将原始数据Y代入,发现其预测错25个,准确率为84.47。
简单二分类的预测结果并不令人满意,故选择更换二分类函数的线性部分。考虑到这部分是一个超平面,且是通过欧式距离计算平面与数据点的距离[4]。
将欧式距离优化为几何距离,引入 SVM 的模型架构,SVM 的超平面如图2所示。选择 C-SVM 分类器,其是二分类支持向量机,通过设训练集、选取合适的核函数K(x,x′)和适当的参数C,构造并求解最优问题,通过设立计算阈值并构造决策函数:
该模型的重点在于调节核函数和参数C。接下来,结合Matlab软件,对模型进行解算。

图2 SVM的超平面
将数据按1∶4划分为训练集和测试集,核函数选取线性核函数K(x,x′)=xTx,参数C定为6。训练完毕后得到准确率为96.610 2%。Box可视化图如图3所示,测试样本准确图如图4所示。
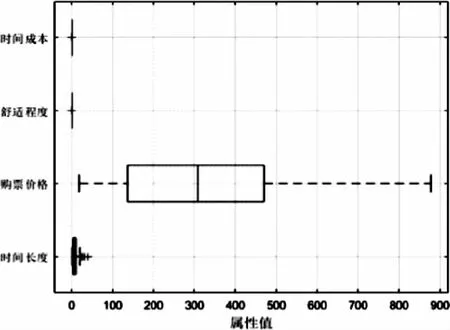
图3 Box可视化图
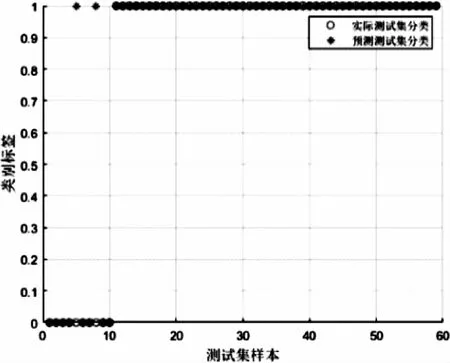
图4 测试样本准确图
本研究希望能通过不同的角度来考察自变量与自变量之间的关系,因此,用灰色关联度 T 检验分析对影响乘客购票行为的自变量关系。考虑到 T 检验是关于时间变化的,所以,将 Excel 表格数据按照乘客购买火车票还是购买高铁票的行为按照时间长度进行分类排序,再根据 CCA 方法,筛选出的4个主要因素时间长度、购票价格、舒适程度和时间成本,并加以分析。其中,时间长度为因变量,其余3个因素为自变量,主要分析自变量与因变量之间的关系。
灰色关联度 T 检验分析的基本思想为按照因素的时间序列曲线和相对变化势态的接近程度来计算关联度,对于离散时间序列,所谓两曲线的相对变化势态的接近程度,是指两时间序列在对应各时段Δtk=tk-tk-1(K=2,3,...,n)间各变量经标准化后的增量大小来判定的。若在时间段Δtk间两增量相等或接近于相等,则这两时间序列在时段Δtk间的关联系数就越大,反之就小。两时间序列的关联度定义为:各时间段Δtk间的关联系数的加权平均数,权数为Δtk。
通过Matlab计算得到,在选择乘坐高铁的乘客中,时间长度对购票价格、舒适程度和时间成本的关联度为-0.035 9,0.011 2和0.007 9。在选择乘坐火车的乘客中,时间长度对购票价格、舒适程度和时间成本的关联度为-0.011 3,-0.009 3 和 0.030 5。很明显,时间长度对于其他3个变量的影响对于乘客购票选择高铁还是火车是不同的。对于选择高铁的乘客来说,时间越长,对舒适程度越为看重;对于选择火车的乘客来说,时间越长,就越不关心舒适程度。对于二者来说,时间越长,乘客会选择较低的票价,并且所有乘客对于出行花费的时间都很重视。
希望能够建立某种准则反映学生购票行为,对于学生购票行为进行综合评价打分,根据CCA分析之后得到的函数表达式的系数,对系数进行AHP层次分析法,得到的系数如表2所示。

表2 AHP权重系数
运用两种方法检验 AHP 层次分析法可行性。
方案1:根据一致性指标公式进行判断。由于共有 8 个自变量,故 n=8。得到 CI=0.130 6,非常接近 0。随机相关一致性 RI=1.41,CR=0.092 6<0.1,AHP 层次分析法结果满足检验。
方案2:用模糊综合评价法进行分析。首先,确定因素集,也就是评价指标,根据CCA分析结果,选出4个主要因素进行模糊综合评价。确定因素集,也就是评价指标U={行驶时间长度,购票价格,舒适程度,时间成本},然后确定评语集V={非常重要,重要,一般,不太重要}。根据AHP层次分析确认各因素权重,确定模糊综合评价矩阵对各因素做出评价,进行矩阵合成运算。最终求得在顾客购票行为因素中,行驶时间长度因素非常重要,购票价格因素重要,时间成本一般,舒适程度因素不太重要。
4 模型的评价
C-SVM 是一种有坚实理论基础的新颖的小样本学习方法。对于本文中的样本较少,逻辑数据和数值数据分布不清的问题,特别适用 SVM 模型进行求解。C-SVM模型的最终决策函数只由少数的支持向量所确定,计算的复杂性取决于支持向量的数目,而不是样本空间的维数,降低了过拟合的风险。但是SVM也有不足之处,SVM 算法对大规模训练样本难以实施。
经典的支持向量机算法只给出了二类分类的算法,而在数据挖掘的实际应用中,一般要解决多类的分类问题。只能通过多个二类支持向量机的组合来解决,势必会增加误差的累计,最终使得预测结果偏差较大。

