综合管廊内燃气管道热平衡及方形补偿器计算

李宏宇， 许淑惠， 马博洋， 李浩天， 徐荣吉， 冯萃敏

(北京建筑大学 北京建筑能源高效综合利用中心，北京100044)

1 概述

燃气管道是压力管道，管道内的燃气与外部环境存在温差，燃气管道会因此受到膨胀力或收缩力，主要采用自然补偿法对管道的应力变化进行补偿。黄鉴等[1]应用有限元分析软件ANSYS对燃气管道钢质弯头在内压作用下的状态进行有限元分析，得到弯头在不同内压下的应力分布。古春雷[2]针对民用建筑燃气管道的应力进行了分析。杨小伟[3]结合工程实例，探讨了埋地燃气管道承受公路荷载的应力计算和校核方法，提出了抗荷载的防护措施。刘艺[4]应用管道应力计算软件计算了随桥敷设的燃气管道的一次、二次应力。陈乐[5]对大直径薄壁燃气管道的应力计算理论、计算方法进行了研究和分析。万文东等[6]采用有限元和数值理论方法，对多因素影响下的燃气管道分支口处弯管应力和变形进行模拟分析。上述文献对燃气管道应力的研究主要是从计算方法、理论方面进行的，对于管道补偿器实际的应力计算分析几乎没有。

综合管廊中的燃气管道采用金属管道，补偿方式一般采用自然补偿，自然补偿的曲率半径直接关系到管廊土建投资及地下空间占有量。由于地下综合管廊地下空间相对狭小，在燃气管道入廊设计中，燃气管道的自然补偿的曲率半径是否满足应力需求，对设计的安全性、管廊的土建成本等影响重大。本文基于某实际综合管廊的燃气管道，此燃气管道靠近门站，燃气温度较低，对表面涂有防腐层的燃气管道建立热平衡方程，获得燃气管道的壁面温度，用弹性中心法对燃气管道补偿器进行应力计算。

2 管廊中燃气管道热平衡计算

2.1 热平衡方程式

以综合管廊中燃气管道为研究对象，建立热平衡方程，求得管道与燃气及管道与空气间的表面传热系数，并考虑管道与管廊的辐射换热和管外的水凝结放热，求得极端环境(此处指极端最高空气温度)下管道温度，为自然补偿应力计算提供计算依据。

由于管廊燃气舱内燃气管道表面与管内燃气温度较低，以燃气管道为研究对象，分析其能量传递情况。管壁为金属，忽略管壁的导热热阻。由于在极端情况下，管廊燃气舱内空气与燃气管道、燃气管道与燃气之间的温差均远大于沿轴向管道自身的温度变化，所以忽略管道的温度变化，忽略防腐层热阻，建立热平衡方程如下：

Φ1+Φ2+Φ3=Φ4

(1)

式中Φ1——管廊壁面对燃气管道外壁的辐射换热量，W

Φ2——管廊内空气与管道外壁间的对流换热量，W

Φ3——管道外壁水凝结过程中换热量，W

Φ4——管道内燃气与管道内壁之间的对流换热量，W

2.2 对流换热计算

① 空气与管道外壁间的对流换热

在管廊燃气舱内，空气温度高于燃气管道外壁温度，由于管廊内采用机械送风，因此空气会以强制对流换热的方式将热量传递给燃气管道。Φ2计算式[7]101为：

Φ2=h1A1(Ta-Tg)

(2)

式中h1——燃气管道与空气的表面传热系数，W/(m2·K)

A1——燃气管道外表面积，m2

Ta——极端环境下的空气温度，K

Tg——燃气管道温度，K

(3)

式中Nu——努塞尔数

λa——空气的热导率，W/(m·K)

L——特征长度，取管道长度，m

燃气管道与空气的对流换热属于外掠圆管对流换热，努塞尔数Nu公式[8]为：

(4)

式中Re——雷诺数

Prf——在空气温度下的空气普朗特数

Prw——在管道外壁温度(即管道温度)下的空气普朗特数

② 管内燃气与管壁间的对流换热

管内燃气与管壁间的对流换热量Φ4计算式[7]153为：

Φ4=h3A2(Tg-Tr)

(5)

式中h3——燃气管道与燃气的表面传热系数，W/(m2·K)

A2——燃气管道内表面积，m2

Tr——燃气温度，K

(6)

式中λg——燃气的热导率，W/(m·K)

管内燃气与管壁间对流换热属于管内受迫对流换热，且属于加热流体的情况，因此Nu用下式进行计算[7]150：

Nu=0.023Re0.8Pr0.4

(7)

式中Pr——燃气的普朗特数

2.3 辐射换热

在燃气管道和管廊壁面进行辐射换热的过程中，燃气管道可视为非凹表面，并且管廊壁面面积远大于燃气管道外径，此时辐射换热模型可视为包容体模型，则Φ1计算式[7]224为：

(8)

式中ε——燃气管道表面发射率

σ——斯忒藩-玻尔兹曼常量，W/(m2·K4)，取5.67×10-8W/(m2·K4)

TL——管廊内壁面温度，K

2.4 燃气管道水凝结放热

由于燃气管道外表面温度低于空气温度，且低于空气露点，所以围绕在管道外围的空气中的水分会释放汽化潜热以凝结水的形式附着在管壁上，且管道外围的空气以及附着在管道外壁的凝结水温度也会逐渐降低。所以此过程管道所吸收的热量为两部分，一部分为潜热换热量，另一部分为显热换热量。水凝结过程潜热换热量Φ3计算式[9]为：

Φ3=(2 500-2.35td)(d2-d3)qm

(9)

式中td——露点，℃

d2——管道外围初始状态下空气的含湿量，g/kg

d3——管道与空气换热结束后外围饱和空气的含湿量，g/kg

qm——管道周围干空气的质量流量，kg/s，取管廊干空气质量流量的10%

d3是根据管壁凝结水的实测温度，查焓湿图得到的，故忽略凝结水显热变化。

(10)

式中qm,q——管廊空气中水蒸气的质量流量，kg/s

qm,g——管廊空气中干空气的质量流量，kg/s

(11)

式中qm,a——管廊中空气的质量流量，kg/s

Vl——管廊的容积，m3

Vg——管廊内燃气管道的体积，m3

ρa——空气的密度，kg/m3

N——换气次数，h-1

qm,a=qm,q+qm,g

(12)

3 管道方形补偿器受力分析及应力计算

方形补偿器的受力计算包括以下内容：选定补偿器形式和尺寸，确定其补偿能力；计算补偿器的弹性力；进行应力计算。

利用弹性中心法计算方形补偿器的应力。对称置于固定支座A、B间有光滑弯弯管方形补偿器的受力计算图见图1，图1中x轴和y轴的坐标原点为O点[10]176。

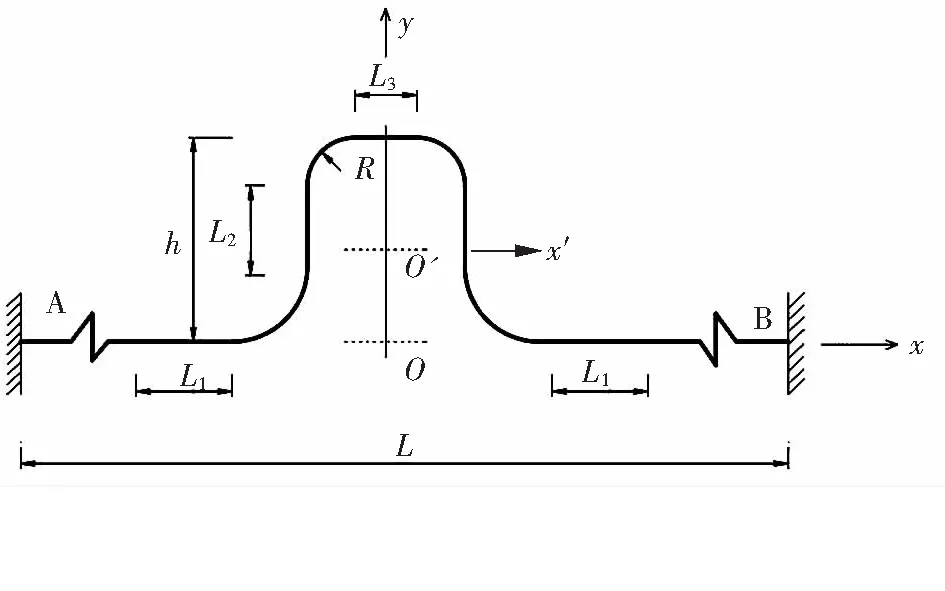
图1 方形补偿器受力计算图

图中h——方形补偿器的外伸臂高，m

L——计算管段的长度，m

L1——方形补偿器两边的自由臂长，m,取值为40倍的管道公称直径

L2——方形补偿器外伸臂直管段长度，m

L3——方形补偿器宽度边的直管段长度，m

R——弯管曲率半径，m

3.1 计算管道热伸长量

固定支架之间管道的热伸长量Δx用下式计算[11]：

Δx=αL(T1-T0)

(13)

式中 Δx——固定支架之间管道的热伸长量，m

α——管道的线膨胀系数，K-1

T1——管内流体最高温度，K

T0——管道安装时的温度，K

3.2 确定弹性中心坐标

弹性中心位于O′点(见图1)。由于方形补偿器外形尺寸对称，弹性中心的横坐标x0′=0，其纵坐标用下式计算[10]177：

(14)

式中y0′——方形补偿器的弹性中心纵坐标，m

K——弯管柔性系数

Lz——方形补偿器的折算长度，m

(15)

式中λ——弯管尺寸系数

(16)

式中δ——管道壁厚，mm

rP——管道平均半径，mm

(17)

式中Dw——管道外直径，mm

(18)

3.3 计算弹性力

燃气管道方形补偿器有x轴和y轴两个方向的弹性力，由于y轴方向的弹性力很小，可以只考虑x轴方向的弹性力，并用其代替x轴和y轴两个方向的合力，即弹性力。弹性力和管段变形之间的关系用下式表达[10]177：

(19)

式中Ft——方形补偿器的弹性力，N

E——钢管的弹性模量，MPa

I——钢管断面惯性矩，cm4

I1——折算管段(即固定支座A、B间的管段)对x′轴(方形补偿器的弹性中心横坐标方向)的线惯性矩[10]34，m3

(20)

(21)

3.4 计算最大弯矩

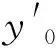
(22)

式中Mmax——弹性力作用下的最大弯矩，N·m

3.5 计算并校核弯曲应力

管道最不利截面处的弯曲应力σw最大，用下式计算[10]176：

(23)

式中σw——管道最大弯曲应力，MPa

n——弯管应力增加系数

W——管道抗弯截面系数，cm3

光滑弯管应力增加系数用下式计算[10]174：

(24)

管道抗弯截面系数W用下式计算[10]170：

(25)

如果计算得到的弯曲应力小于许用外载综合应力[σw]，则安全，因此只要σw≤[σw]则证明安全。[σw]按下式计算[10]166：

[σw]=1.2σ1+0.2σ2

(26)

式中 [σw]——许用外载综合应力，MPa

σ1——环境温度下钢材的许用应力，MPa

σ2——钢材表面温度下钢材的许用应力，MPa

4 实际案例计算

本实际管廊位于北京市，管廊长200 m，宽1.9 m，高2.8 m。廊内空气温度取极端最高空气温度41.9 ℃，相对湿度为76%，露点为34.9 ℃，含湿量为36.48 g/kg。查焓湿图得：当管道外围空气相对湿度为100%，温度为露点34.9 ℃时，含湿量d2=36.48 g/kg；当管道外围空气相对湿度为100%，干球温度(取凝结水的实测温度)为10 ℃时，含湿量d3=7.638 g/kg。空气温度为41.9 ℃时的空气运动黏度为15.6×10-6m2/s，普朗特数为0.703，热导率为0.025 9 W/(m·K)。换气次数为3次/h。气压为标准大气压。管廊内壁面温度为20 ℃，管廊内风速为0.167 m/s。

此管廊靠近门站，燃气舱内布置有一条中压管道和一条次高压管道，表面均涂有防腐层。燃气管道及燃气(天然气)的计算参数见表1。

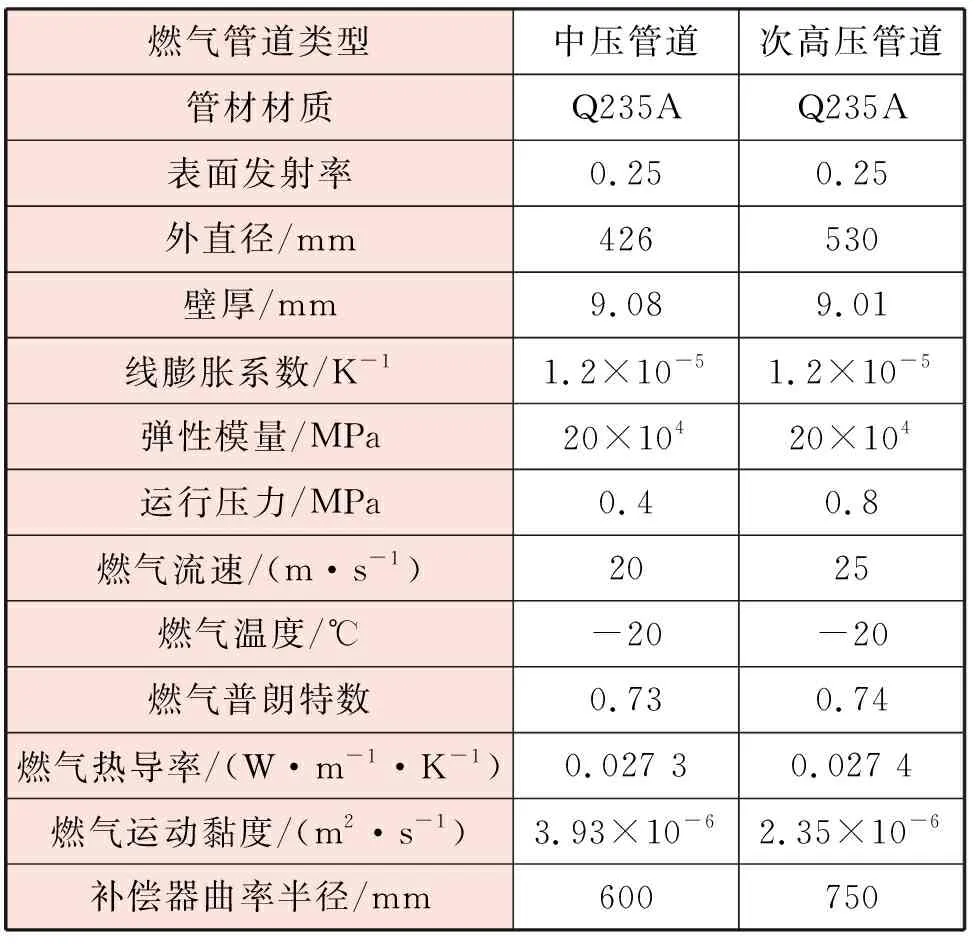
表1 燃气管道及燃气的计算参数

将相关参数代入上述公式中得到计算结果，见表2。

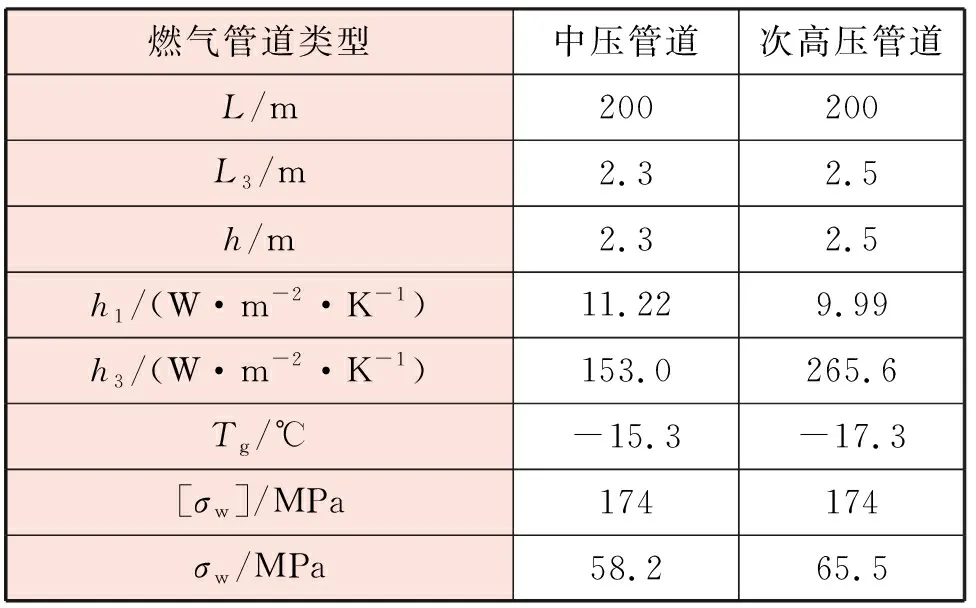
表2 计算结果

该燃气舱内中压管道与次高压管道均满足σw≤[σw]，即当燃气管道方形补偿器曲率半径为1.5倍管道公称直径时，管道的应力满足要求。

5 结论

① 对综合管廊内有防腐层的燃气管道建立热平衡方程，获得燃气管道的壁面温度。

② 用弹性中心法对燃气管道方形补偿器进行应力计算。

③ 结合实际案例计算了某极端环境(极端最高空气温度)下燃气管道的壁面温度，以及方形补偿器曲率半径为1.5倍管道公称直径时的应力。结果表明：管道壁面温度较低，与管内燃气温差较小；在极端环境下选择自然补偿，当方形补偿器曲率半径为1.5倍管道公称直径时，管道的应力满足要求。