一种复合材料桅杆的优化设计

欧阳可汉，易周航，郑 浩

（1.海装沈阳局驻葫芦岛地区军事代表室，辽宁葫芦岛125004；2.华中科技大学 船舶与海洋工程学院，武汉430074）

0 引言

桅杆是船舶结构中的重要组成部分，传统桅杆一般是木质的长圆竿或金属柱，通常从船的龙骨或中板上垂直竖起，用来悬挂船帆和旗帜，或装设天线、雷达和瞭望台等。随着人类对海洋开发的进一步加深，对船舶结构的要求也在逐步提高，但传统的桅杆受制于材料特性，其性能已无法满足船舶技术的发展需要;与传统的船舶制造材料相比，复合材料的优势非常显著。复合材料以其强度高、质量小、耐腐蚀、耐磨损等特点，在制造高质量船体方面远超传统材料，其还具有无磁性干扰、冲击韧性良好、隔热性能好等特点，与现代电子信息技术的发展相辅相成，更契合现代船舶发展的需求。此外，以复合材料造船可以保证船体无缝连接，整体性好。复合材料便于成型加工，在应对复杂结构方面有不小优势。复合材料船舶制造工序更加简便省力，便于批量生产，在资金要求巨大的船舶行业，控制制造成本和时间成本能极大促进行业资金流动、提升行业景气程度。同时，复合材料相对于传统材料而言，船舶结构维修保养会更加简单，随之而来的是船舶使用寿命的延长[1]。因此，本文面向复合材料桅杆展开了设计及优化工作。

就船舶桅杆而言，从风帆时代悬挂船帆的木制桅杆，到近代布满天线雷达的钢铁桅楼，再到如今电子设备高度集成的复合材料桅杆，其功能日趋丰富，而结构却删繁就简，成为如今一柱擎天的模样[2]。作为船舶结构的重要部分，桅杆结构已有不少相关研究。王燥春等[3]讨论了风载荷、惯性载荷、重量载荷和螺旋桨激励等对铝合金桅杆的影响。郎济才等[4]借助ANSYS对筒状桅杆仿真建模并进行模态分析计算，在建模过程中探讨了杆上集中质量和边界条件的影响，并与实际模型试验结果进行对照检验。杨振材等[5]简化了筒状桅杆仿真建模时的边界条件，随后对简化模型因风导致的桅杆振动问题进行了讨论。高靖等[6]借助ANSYS及相关知识对桅杆雷达罩的复合材料夹层板及钢质部分进行了强度和刚度的校核并选取了合适尺寸的复合材料板。杨娜娜等[7]结合理论和数值研究对桅杆结构中的复合材料夹层板进行了稳定性分析并与试验对比，验证了数值方法在该问题上的可行性。徐珊珊[8]从材料及结构上对综合集成桅杆进行抗爆及防护特性研究。吴超等[9]讨论了3种主要载荷影响下的桅杆结构应力分布。沈刚强等[10]测试了原料为乙烯基树脂和高强玻璃纤维布压铸成型试件热老化试验后的力学性能，借助ANSYS估算了复合材料桅杆的耐候性。位莎[11]则通过流固耦合计算，研究了多种桅杆的风载特性；张营川[12]研究了桅杆裹冰状态下涡激振动问题。

1 设计过程

1.1 设计原则

复合材料层合板的铺层设计方案是由纤维和基体所组成的单层材料性能所决定的，层合板中各单层材料的纤维取向、铺层顺序、各铺层角度相对于总层数的比例和总层数均会影响层合板的整体性能。设计原则应该力求以最少的铺层和最小的质量而达到最优的性能[13]。

1）铺层均衡对称，避免层合板固化后翘曲变形。

2）铺层数应尽量少，以减小二次应力。

3）铺层取向应尽量按照承载方向设计。0°铺层承受轴向载荷，45°铺层承受剪切载荷，90°铺层承受横向载荷和控制泊松比。

限制同角度铺层的，最大连续铺层不超过3层，以减少层间开裂和边缘分层，表面铺设±45°铺层以改善层合板的抗压缩和抗冲击性能。

1.2 设计过程

Abaqus是一套功能强大的通用有限元软件。作为通用的模拟工具，Abaqus拥有可模拟任意几何形状的单元库和各种类型的材料模型库，包括复合材料。Abaqus是本文优化工程中使用的主要工具。

1.2.1铺层层数影响

模型高10 000 mm，外径200mm复合材料圆筒，铺层角度以0°（绕轴方向）和90°（沿轴方向）依次交替，铺层厚度为0.2mm。模型底部为全约束，顶部施加水平方向1 000 N 集中力，并在全局施加一个垂直向下的加速度−9 800 mm/s2，如图1所示。

图1 复合材料圆筒约束及载荷

以下是铺层30层增至50层圆杆的响应，如表1、图2和图3所示。

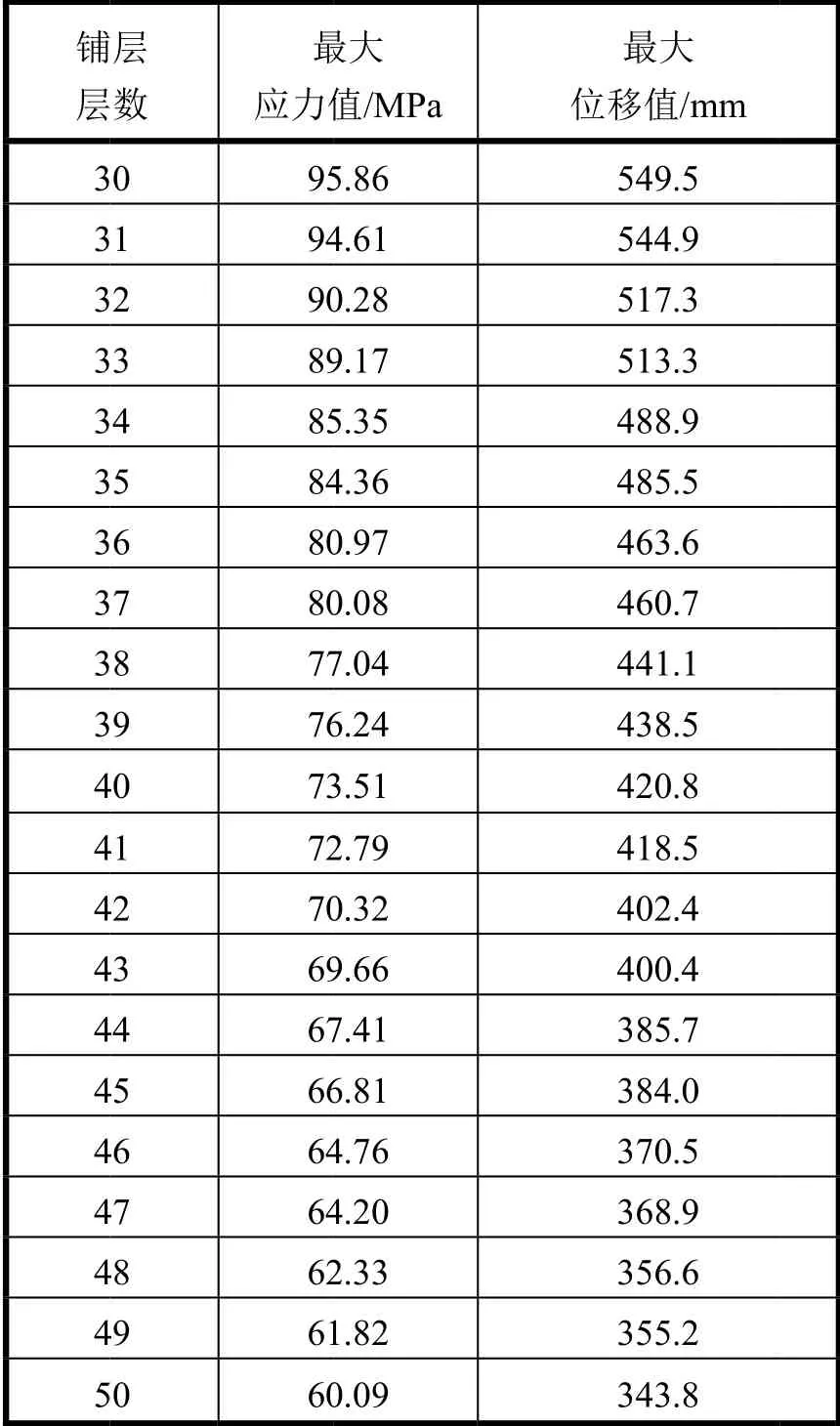
表1 不同铺层层数的圆杆响应

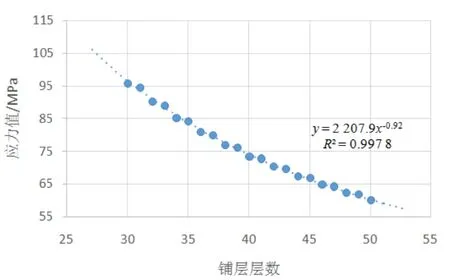
图2 铺层层数与最大应力

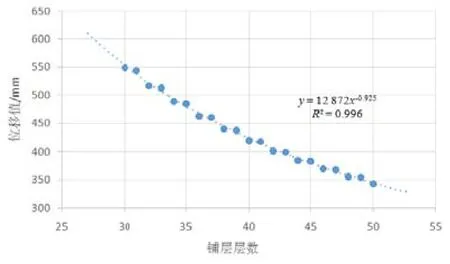
图3 铺层层数与最大位移

从表1、图2和图3可以发现，随着铺层层数的增加，圆杆在受到外载荷时的最大应力和最大位移都在降低，但是趋势减缓；此外，随着铺层层数的增加，仿真结果离趋势线越来越近，这是因为该边界条件下复合材料圆杆的强度主要由沿轴方向的铺层提供，增加绕轴方向的铺层并不能明显提升其强度，但随着铺层层数增多或是减少铺层厚度都可以有效使得仿真结果更逼近趋势线。

1.2.2铺层角度影响

模型高10 000mm，外径200mm复合材料圆筒，铺层角度以0°（绕轴方向）和90°（沿轴方向）依次交替共50层，铺层厚度为0.2mm。模型底部为全约束，在全局施加一个水平方向19 600 mm/s2的加速度和一个垂直向下的加速度−9 800mm/s2，如图4所示。

图4 复合材料圆筒约束及载荷

以最内层铺层为基准，以下是铺层角度由0°偏转至90°圆杆的响应，见表2、表3和图5～图7所示。

表2 不同铺层角度的圆杆响应

图5 铺层角度与最大应力

图6 铺层角度与最大位移

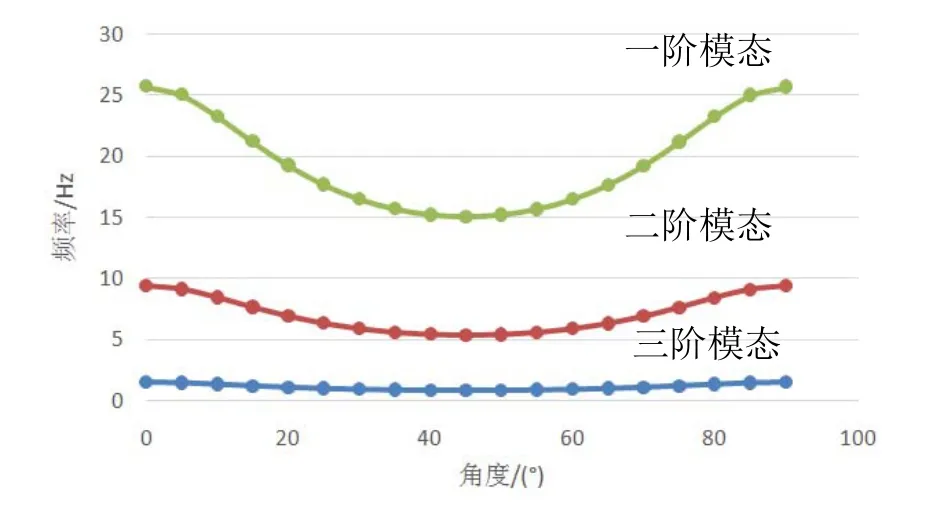
图7 铺层角度与固有频率

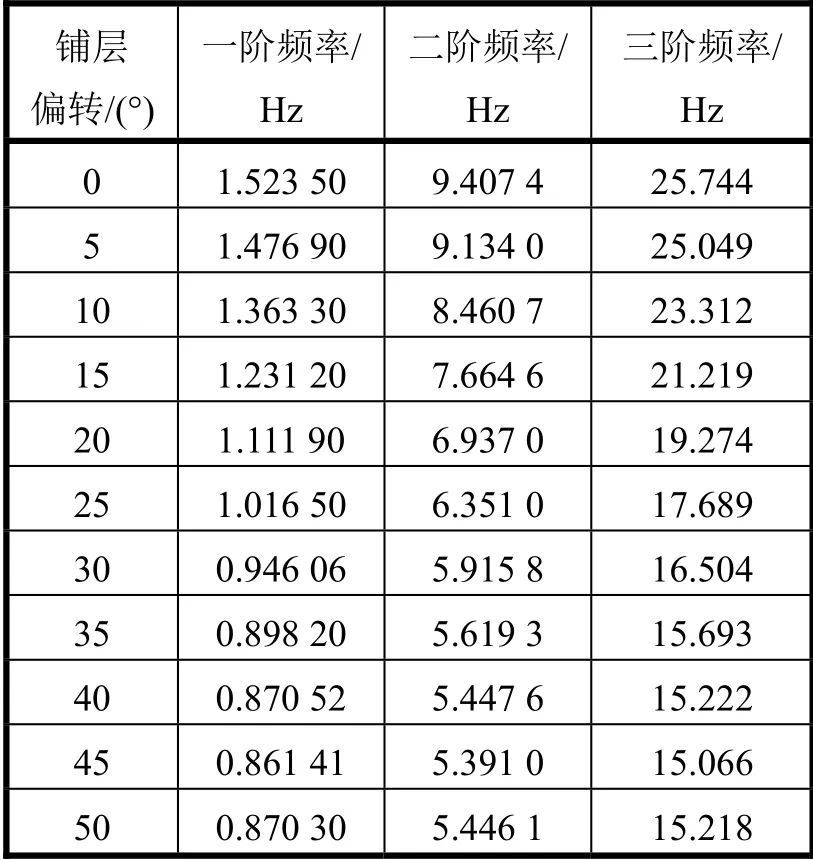
表3 不同铺层层数的圆杆模态

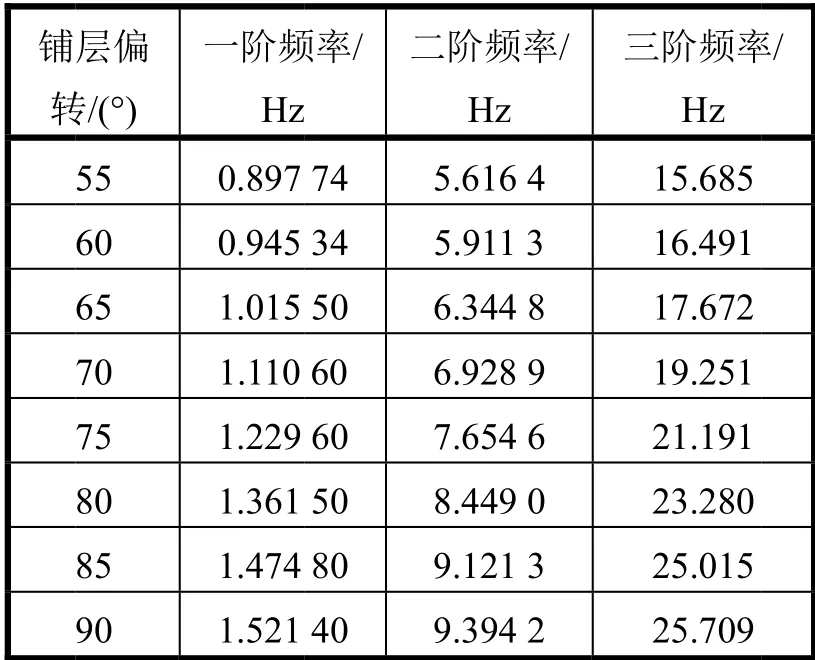
续表3：

由表3可知，铺层角度偏转45°时，最大应力相对于其他角度最小，但是最大位移却最。由此说明，±45°铺层能有效承受水平方向的载荷，但变形会很大。在铺层角度为0°、90°时，最大应力相对于±45°的铺层角度更大，但是变形会更小。这说明±45°的铺层方式强度更高、刚度更差，0°、90°的铺层方式刚好与之相反，这也可以从模态计算的结果进行佐证。此外，从结果而言，要极力避免20°和70°的铺层角度，该角度的铺层不但强度表现极差，而且刚度也较差。

2 优化结果

所用材料均为玻璃钢纤维，材料属性如表4所示。

表4 材料属性

原始杆型模型高15 000 mm，底端内径9 0 m m，首端内径40mm，均匀变化，壁厚10mm，铺层方式为0°、90°交替铺层，如图8所示。

图8 原始型号模型

优化杆型模型高15 000mm，均分为5段，第1段（固定段）内径90mm，厚10mm；第2段内径74 mm，厚8 mm；第3段内径60 mm，厚7mm；第4段内径48 mm，厚6 mm；第5段内径38mm，厚5mm。铺层方式为内侧0°、90°交替铺层，仅最外侧为±45°铺层，如图9所示。

图9 优化型号模型

两模型底部均为全约束，考虑到12级风力对应风压644.25 Pa 到911.71 Pa，因此对受风面加载0.000 9MPa，并在全局施加一个方向垂直向下的加速度−9 800mm/s2，如图10所示。

计算结果如图11和图12所示。

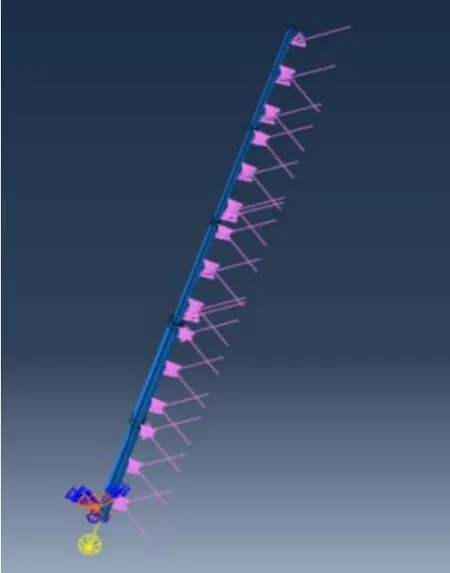
图10 边界条件与外载荷

图11 应力计算结果

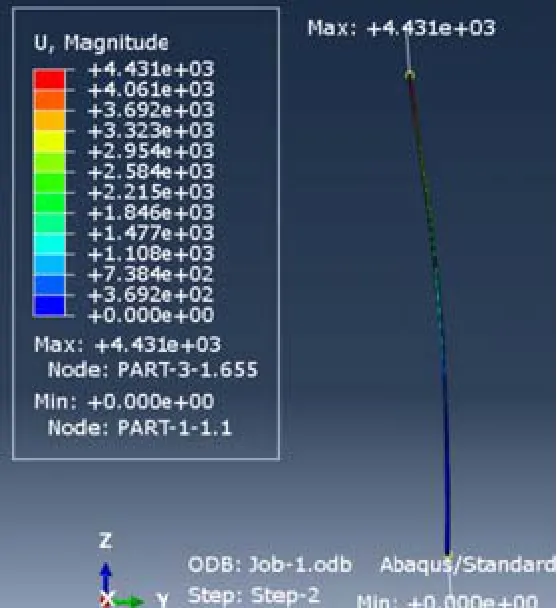
图12 位移计算结果

该工况下，模型的最大应力位于第1段于第2段相交处，为192.8MPa，而根部最大应力为151.4MPa。模型最大变形在顶部，为4 431mm。

模态计算结果如图13～图15所示，分别为优化型前三阶模态。

图13 一阶模态

图14 二阶模态

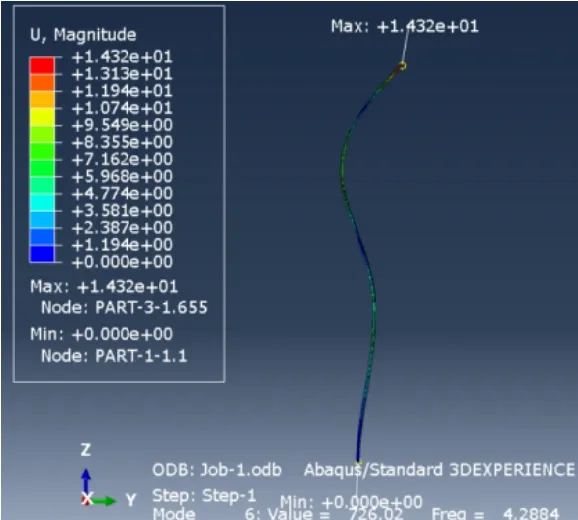
图15 三阶模态

表5为原始型与优化型的计算结果。

表5 结果比较

3 结论

借助Abaqus分析了原始杆型和优化杆型各自的特性：

1）就应力而言，优化型最大应力位置不在桅杆底端，而是处于第1段与第2段相交位置，应力较大，主要因结构突变带来应力集中，应当尽量避免；而优化型底端最大应力为151.4 MPa，相较于原始型号的应力（148 MPa），优化型应力的增大不明显，且也未超过设计应力。

2）就变形而言，优化型不如原始型，但处在合理范围内。主要原因是除第1段以外，其余段的铺层厚度均小于原始型。

3）就固有频率而言，优化型1阶固有频率高于原始型，其余低于原始型。

4）就质量而言，优化型重量远小于原始型，优化效果明显，满足优化初衷。

5）就加工而言，原始型为圆台状杆型，因此在实际加工中，0°、90°铺层很容易发生倾斜，从而使强度和刚度大打折扣。而优化型5段圆柱型结构不仅避免了上述问题，还方便加工运输。