小卫星增阻主动离轨技术的设计与实践

陈险峰， 任维佳， 刘惟芳， 李晓明

(长沙天仪空间科技研究院有限公司， 长沙410205)

1 引言

随着商业航天的蓬勃发展， 近几年进入轨道的卫星， 特别是低轨小卫星， 已呈现爆发式增长的趋势。 低轨卫星发射数量连续几年大幅增长。从已经发布的计划看， OneWeb 计划发射900 颗卫星， 波音公司计划发射2956 颗， 三星公司计划发射4600 颗， SpaceX 公司的StarLink 卫星数量更是达到惊人的11943 颗， 仅此一项计划就超过了目前在轨卫星总数。 我国多家航天单位发布的低轨星座计划， 总数也达到了上千颗。 大量的低轨星座计划， 特别是轨道高度基本集中在500 ～1200km 之间， 一旦逐渐开始部署， 将大大增加彼此碰撞的风险。 2009 年2 月10 日， 美国铱星33号卫星和俄罗斯宇宙2251 卫星在800km 的轨道高度相撞， 产生了大量空间碎片。 而这些碎片将会进一步增加航天器和碎片碰撞的概率， 如不采取任何措施， 在数十年后， 级联碰撞效应(Kessler Syndrome) 的后果将使近地空间完全被碎片充斥而不能再正常使用。 因此， 这类事件无疑为航天器飞行安全敲响了警钟。

正因为预计此类威胁航天器飞行安全的风险的概率越来越大， 国际机构间空间碎片协调委员会(IADC) 在2002 年正式通过了《IADC 空间碎片减缓指南》， 对限制空间碎片产生的方法进行评估， 并推荐行之有效的技术措施， 对GEO 和LEO 轨道的航天器给出了寿命末期的处置原则。2009 年， 我国印发了《空间碎片减缓与防护管理办法》； 2015 年， 印发了修订版《空间碎片减缓与防护管理办法》。 管理办法规范了航天器研制生产、 发射和在轨运行行为中， 空间碎片减缓和防护管理方面的职责、 措施和要求， 保护航天器在轨运行安全和空间环境。 2018 年， 中国主管部门进一步明确了低轨卫星必须具有离轨手段且在轨时间不超过25 年的要求。

国家对空间基础设施进行管理的层面上密集出台相关要求， 也是基于当前天基互联网等大型低轨星座计划蓬勃发展的现实情况， 通过政策引导， 尽快催生、 成熟和推广普及相关技术。 而本文所述的卫星离轨的相关技术， 不但可以用于离轨， 而且作为一种低成本、 应用灵活的控制手段， 也能够用于低轨卫星星座的相位保持和编队飞行， 对当前天基互联网系统的设计和运行有非常好的借鉴应用价值。

2 不同轨道高度卫星的离轨方法

按运行轨道的高度划分， 卫星运行的轨道主要分为LEO (低轨)、 MEO (中轨)、 GEO (同步) 三种， 每种轨道高度的离轨要求和离轨模式也有很大的不同。

LEO 轨道卫星， 是指轨道高度低于2000km的卫星， 实际范围一般在1500km 以下(范艾伦辐射带的下限)。 离轨方法一般是利用卫星推力器动力或气动阻力， 使卫星减速， 最终坠入大气层烧毁。

利用气动阻力减速， 可以是卫星本体的气动阻力， 也可以通过增大卫星沿速度方向的投影面积， 从而增加阻力， 加快陨落。 这种方法简单易行， 但随着轨道高度的增加， 高层大气密度越来越稀薄， 从而轨道衰减效果越来越差。 同样体积和质量的卫星， 如果运行在500km 轨道高度， 其在轨寿命大约为5 ～20 年； 如果运行在1000km高度以上， 其在轨寿命将达到数百年。

MEO 轨道， 一般是指轨道高度在2000 ～36000km 之间的卫星轨道。 典型的如GPS、 北斗、伽利略卫星， 其轨道高度都在20000km 左右； 还有部分MEO 轨道通信卫星部署在8000 ～10000km轨道。 这些卫星为了对地面提供持续服务， 一般会在同一个轨道面有多颗卫星， 相位均匀分布，形成星座。 因此， 这种卫星的离轨需要解决的主要问题是避免失效卫星对同轨道面其他卫星的影响， 需要在卫星寿命末期通过变轨发动机将其推离工作轨道。

GEO 轨道， 是指距离地面约36000km 的轨道， 其特点是轨道周期为24h， 与地球自转周期相同。 如果轨道面与地球赤道面重合， 则为地球静止轨道， 广泛应用于同步通信卫星。 因此， 地球静止轨道的轨位完全可以用“寸土寸金” 来形容， 其对即将失效卫星的离轨要求也是最高和最明确的。 在IADC 减缓指南中已明确相关要求，即卫星需离轨至特定的“弃置轨道”， 约定了卫星在一定引力摄动、 太阳辐射压力下的轨道高度要求。 如下:

ΔH=200 +35 +1000·CrA/m

其中， ΔH 为相对于地球同步轨道的相对高度； Cr为太阳辐射压力系数； A 为面积， 单位是m2； m 为质量， 单位是kg； A/m 为面质比。

按此条件计算， 同步卫星的弃置轨道一般比同步轨道高约235 ～300km， 使得失效卫星数十年至100 年内轨道最低点不会重新回到同步轨道高度。

因此， 针对不同轨道高度， 离轨的目标不同， 方法也不同。 主要有两种方法， 一是利用气动阻力减速降轨陨落(针对LEO)， 二是利用发动机变轨， 比较如下:

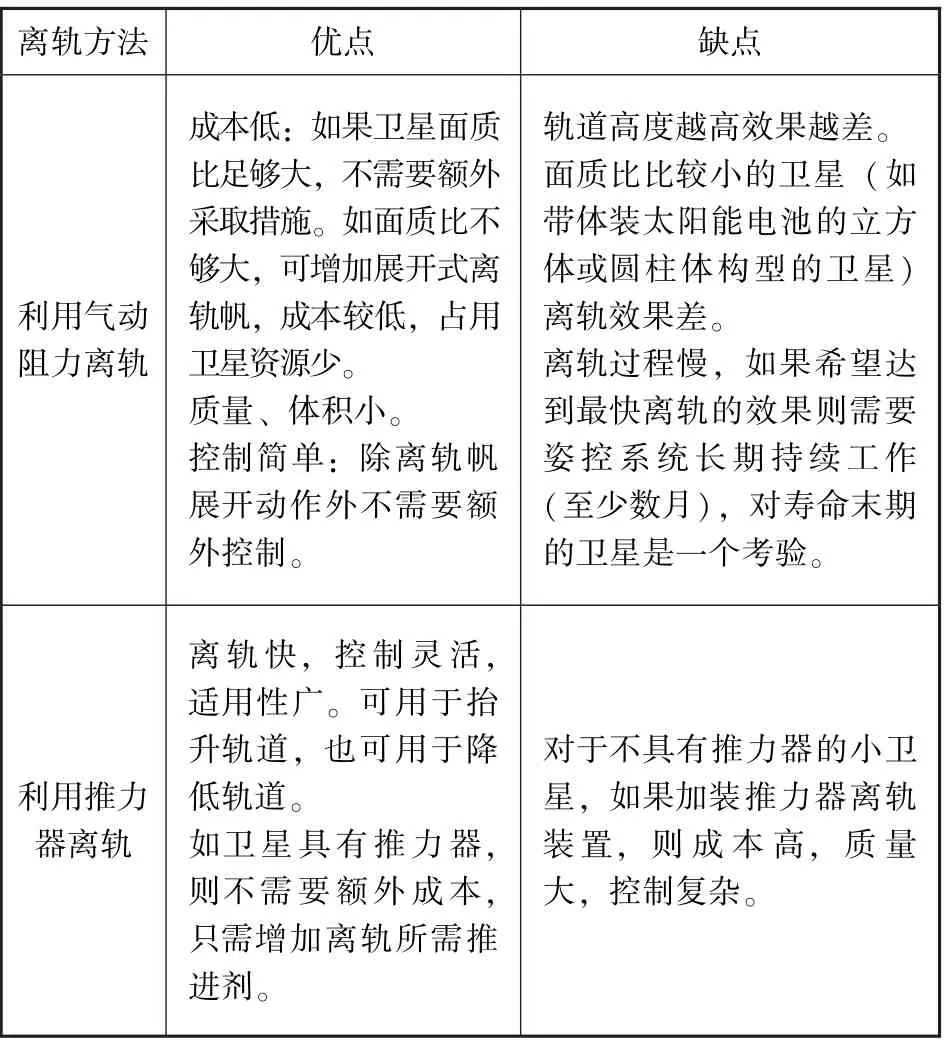
表1 两种离轨方法比较Table 1 Comparison of two deorbit methods

3 利用气动阻力离轨的性能研究

(1) 轨道高度对离轨时间的影响。

假设一颗典型的3U 立方星， 质量是3kg， 平均迎风面积为0.06m2， 面质比为0.02。 使用HPOP 轨道模型计算不同轨道高度时的轨道寿命。

轨道参数:

历元时刻及仿真计算起点为UTC 时2019 年10 月1 日00: 00: 00。 轨道倾角90°。 轨道高度分别为300km、 400km、 500km、 600km、 700km，偏心率为0 的圆轨道。 其他轨道参数均为0。

HPOP 轨道模型参数取值:

太阳辐射指数F10.7 =75

地磁指数Kp=3

太阳辐射压力指数Cr=1.0

大气阻力系数CD=2.2

其他参数及模型均按默认值设置。

经计算， 不同轨道高度的陨落时间如下:

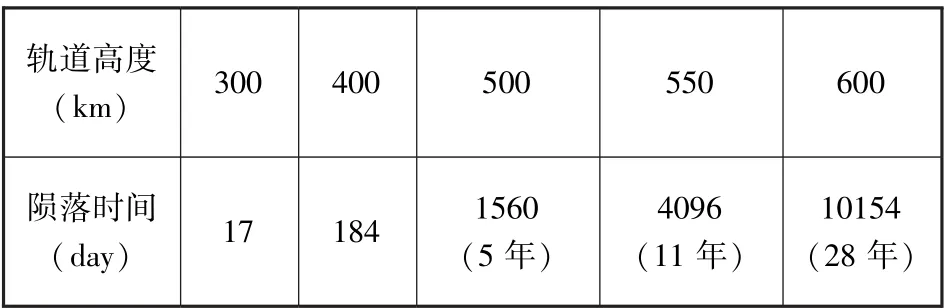
表2 不同轨道高度的卫星陨落时间Table 2 Falling time of satellites at different orbital altitudes

由表中结果可见， 在面质比为0.02 时， 轨道高度超过550km， 陨落时间将会非常长， 已超出低轨卫星任务后在轨时间不应超过25 年的要求。 这是因为轨道高度越高， 大气密度越低，陨落时间也就越长。 大气密度和轨道高度的关系， 有如下曲线:

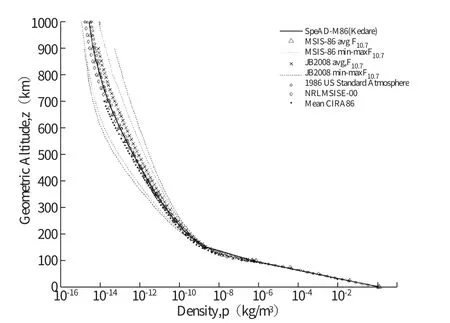
图1 大气密度和轨道高度的关系Fig.1 Relationship between atmospheric density and orbital altitude

由曲线可以看出， 轨道高度从300km 到400km、 从400km 到500km， 大气密度分别降低了大约一个数量级， 而陨落时间也增加了大约一个数量级。 而从500km 到1000km， 大气密度降低了2 个数量级， 1000km 左右轨道陨落时间将达到数百年。

下面计算轨道高度500km 时， 不同面质比时陨落时间。 计算结果如下:

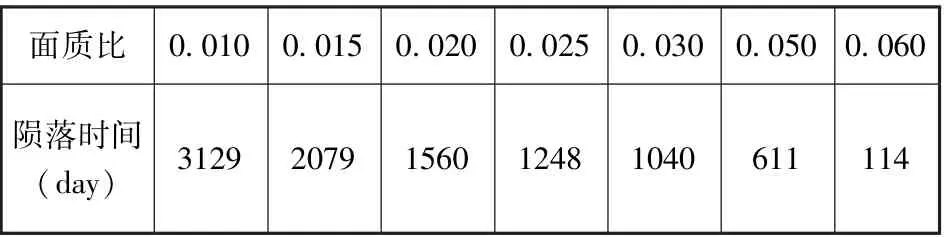
表3 不同面质比卫星的陨落时间Table 3 Falling time of satellites with different area-mass ratio

由上面的算例， 可以得到如下结论:

①利用气动阻力离轨比较适用于550km 高度以下的轨道， 在此轨道高度之上， 因大气更加稀薄， 气动阻力小， 离轨时间将会很长。

②欲使离轨时间在5 年以内， 面质比一般需要达到0.02 以上， 两年以内陨落， 面质比应达到0.05 以上。

4 某立方星离轨帆设计

天仪研究院自研卫星为6U 立方星， 卫星平台为TY 系列通用卫星平台， 根据搭载载荷不同，整星质量在7.7 ～10kg 之间。 使用展开式太阳能帆板， 分离前折叠在星体两侧， 分离后展开。 整体构型如图2 所示:

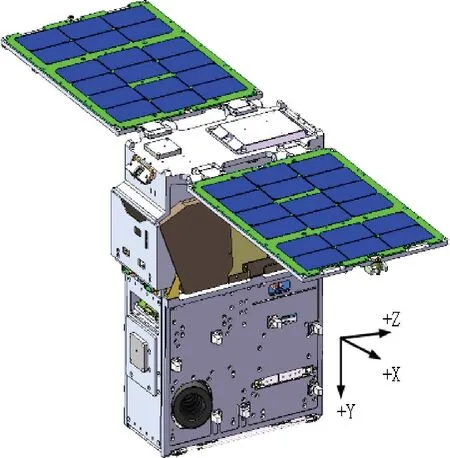
图2 6U 立方星整体构型Fig.2 Overall configuration of 6U cubic satellite

卫星的姿控系统使用星敏感器、 太阳敏感器、 磁强计作为姿态传感器， 使用磁力矩器和动量轮作为姿控执行机构。 在飞行中根据任务模式不同， 有磁控自旋、 惯性指向和对地指向等不同的姿控工作模式。 因此， 在需要离轨时， 可以控制卫星转向， 使最大投影面积指向速度方向， 获取最大减速效果。

在+Y 方向(帆板法向) 指向速度方向时，投影面积最大， 为:

0.59m×0.21m =0.124m2， 卫星质量7.7kg，则面质比为:

0.124/7.7 =0.016 (m2/kg)

按照前面的算例使用的大气参数(F10.7 =75)， 0.016 的面质比陨落时间约为5 年， 仍不足以使卫星在工作结束后实现尽快离轨， 因此， 设计了一块展开式离轨帆。

对离轨帆的要求是:

(1) 在发射前能够折叠， 尽量减小体积， 不改变卫星原有构型；

(2) 卫星任务完成后， 能够顺利展开， 展开后能够保持固定的展开状态；

(3) 展开后的框架应有足够的强度和刚度，在保证支撑能力的同时尽量减小对姿控的影响；

(4) 离轨帆展开状态下有尽量大的面质比。

最终的设计方案是采用两级支撑杆和铝箔帆组成的离轨帆， 折叠在太阳翼底板下部， 释放时熔断拉线， 通过扭簧展开。 离轨帆结构总质量为0.2kg， 展开后总投影面积(含帆板和星体- Y面) 为0.74m2， 展开效果如图3 所示:

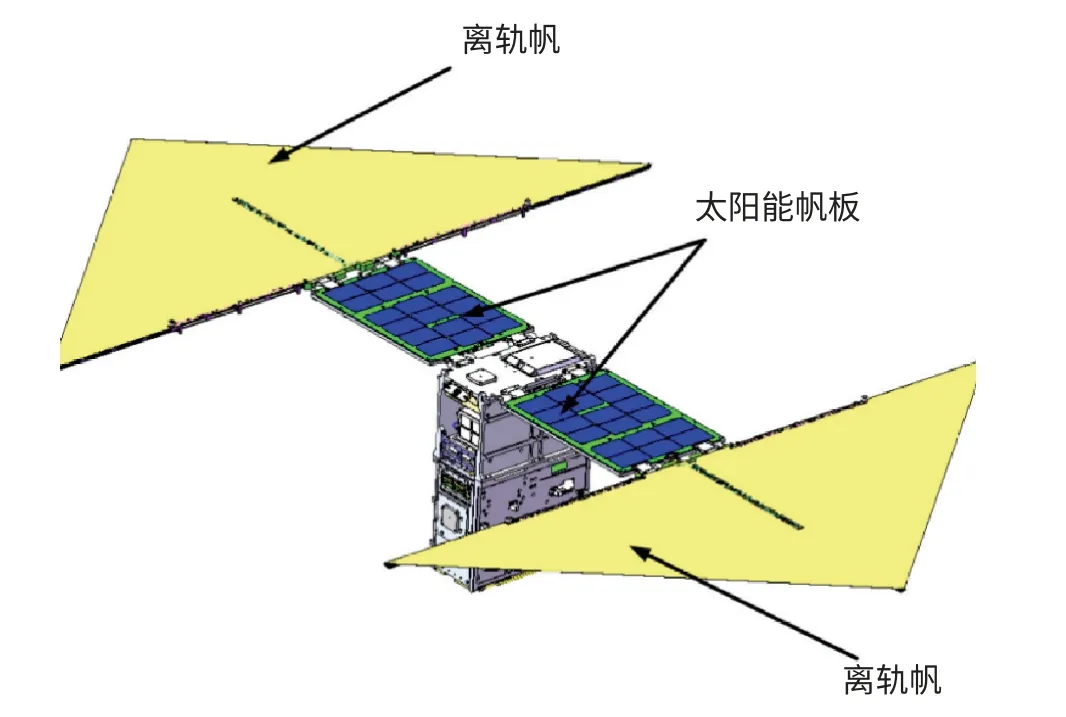
图3 离轨帆展开效果图Fig.3 Effect drawing of the deorbit sail deployment

这种设计， 充分利用了帆板的面积， 在此基础上利用带骨架支撑的铝箔帆， 扩大迎风面积的效率最高， 且结构质量和体积小， 不改变原卫星设计， 对卫星原结构几乎无影响。

离轨帆展开地面试验的情景如图4 所示。

图4 离轨帆展开地面试验Fig.4 Ground test of the deorbit sail deployment

5 离轨帆展开后轨道衰减分析

2019 年1 月21 日， 搭载天仪研究院首个带有离轨帆装置的立方星“潇湘一号03 星” 发射入轨。 2019 年4 月， 卫星完成主要科学试验工作， 展开离轨帆。 从监控相机图像识别， 离轨帆展开正常。 如图5 所示。

图5 离轨帆在轨展开后的监视相机影像Fig.5 Surveillance camera image of the deorbit sail after deployed in orbit

离轨帆展开后， 卫星的工作姿态以卫星绕Z轴自旋、 Z 轴与轨道面垂直的磁控自旋模式为主。因此， 实际等效面质比将比最大投影面积0.74m2要小些。 具体等效面积值， 我们通过实际运行轨道进行推算， 并对陨落趋势进行预测。

首先选取4 月和9 月两个轨道:

4 月30 日两行根数:

表4 4 月30 日轨道两行根数Table 4 Radical of two rows of tracks on April 30

9 月30 日两行根数:

表5 9 月30 日轨道两行根数Table 5 Radical of two rows of tracks on September 30

因为两行根数所用的SGP4 外推模型精度原因， 将SGP4 转换为HPOP 模型进行外推。 两条轨道都外推到UTC 时2019 年10 月1 日00: 00:00， 调整面质比数据， 使这一时刻两个轨道的卫星位置重合， 所使用的面质比数据即为4 月30 日至9 月30 日的平均面质比。

首先对HPOP 的部分大气参数根据实际数据取值， 包括太阳辐射指数F10.7、 地磁指数Kp、太阳辐射压力指数Cr、 大气阻尼系数Cd。

太阳辐射指数F10.7， 按中科院空间环境预报中心的历史数据， 得到4 月30 日至9 月30 日的平均值。 共249 天， F10.7 平均值为68.54。

地磁指数Kp， 是全球范围12 个台站、 每日8个时段测得的地磁扰动强度的标准化指数的平均值， 是用于描述地磁强度总体水平的一个分级值(从0 ～9， 分别表示地磁活动的强度)， 分级值与实际地磁强度呈近似对数关系。 文档[4] 表明Ap(单个地球台站的全日地磁强度指数) 与大气密度在Ap≥50nT 时呈近似线性关系， 而在Ap＜50nT时接近指数关系。 此处参考美国NOAA(国家海洋和大气管理局) 4 月30 日至9 月30 日历史数据， 取Kp=1.5。

太阳辐射压力指数Cr与卫星表面材料相关。在近地轨道上， 因太阳光压在卫星速度方向是正向作用力和反向作用力交替， 因此会使轨道的偏心率增大， 但对卫星整体能量影响不大， 对航天器轨道寿命影响较小， 此处取默认值1.0。

表6 4 月30 日轨道6 根数Table 6 Radical of track 6 on April 30

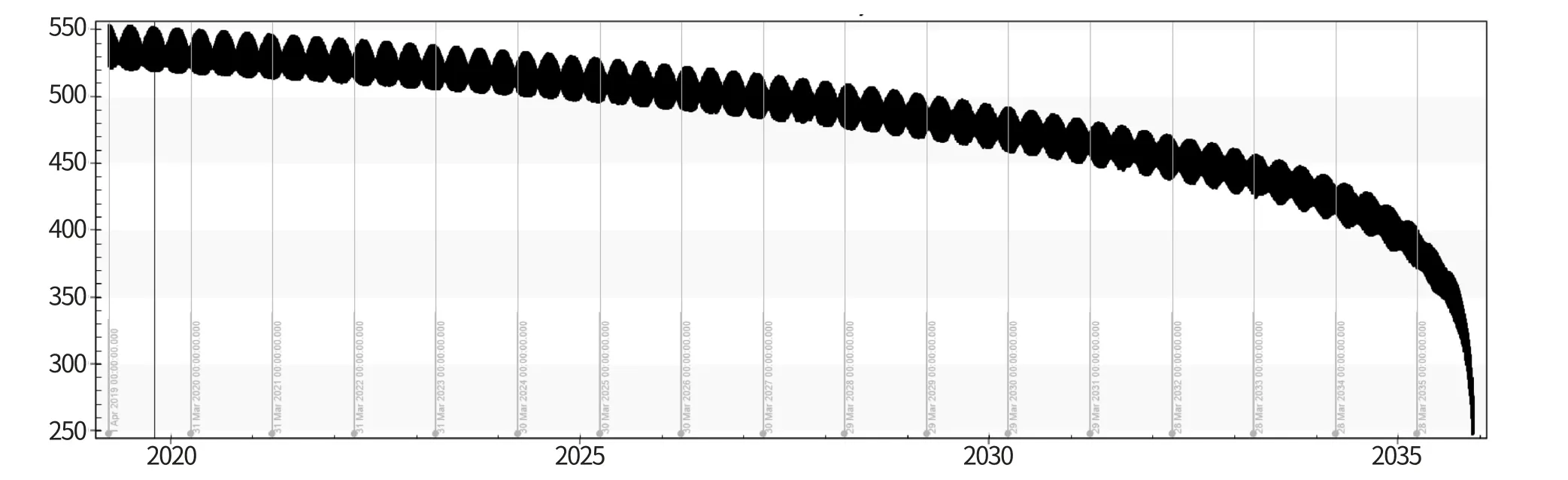
图6 面质比0.016m2/kg 时轨道高度演化Fig.6 Orbital height evolution with area-mass ratio of 0.016m2/kg

大气阻尼系数CD的选取， 一方面是稀薄大气的气面相互作用理论还不完善， 目前大气密度模型误差较大， 另一方面热层大气环境不断变化， 因此很难获得某一时刻较精确的取值。 此处按经验值取低地球轨道的常用取值2. 2。

将4 月30 日两行根数转换成HPOP 轨道6根数:

首先计算如果卫星无离轨帆， 按照0.016m2/kg的面质比， 其他条件不变， 轨道寿命将有多少年。

经计算， 陨落时间为2035 年12 月， 卫星在轨寿命为16 年。

下面对离轨帆展开后的轨道寿命进行估算。

HPOP 外推模型中面质比的推算: 按前述4月30 日和9 月30 日的两行根数， 将4 月30 日的轨道转化为HPOP 轨道， 尽量准确地设置大气参数， 外推到9 月30 日， 考察两条轨道在同一时刻的半长轴， 并通过对4 月30 日轨道设置一定的面质比， 使两条轨道的半长轴一致， 此时的面质比即为4 月30 日到9 月30 日期间的平均面质比。

考虑到卫星在正常工作时， 会在磁控自旋、 对地数传、 对目标指向等多种模式之间进行切换， 每种工作模式的面质比是不同的， 因此得到的面质比应该是最大迎风面时的面质比0.096m2/kg 和最小迎风面时的面质比0.005m2/kg之间。

按上述推算方法， 得到面质比为0.038m2/kg，作为对照， 无离轨帆时的平均面质比0.02m2/kg，有显著增加。

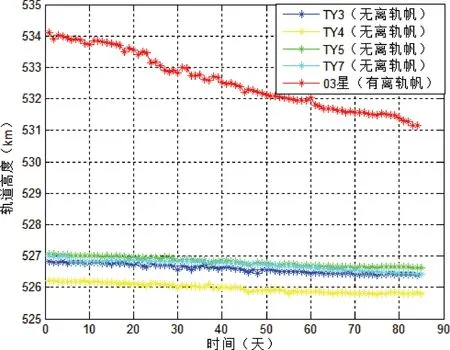
图7 天仪有无离轨道帆6U 标准卫星的轨道高度变化曲线Fig.7 The orbital altitude variation curve of the 6U satellite with or without a deorbit sail

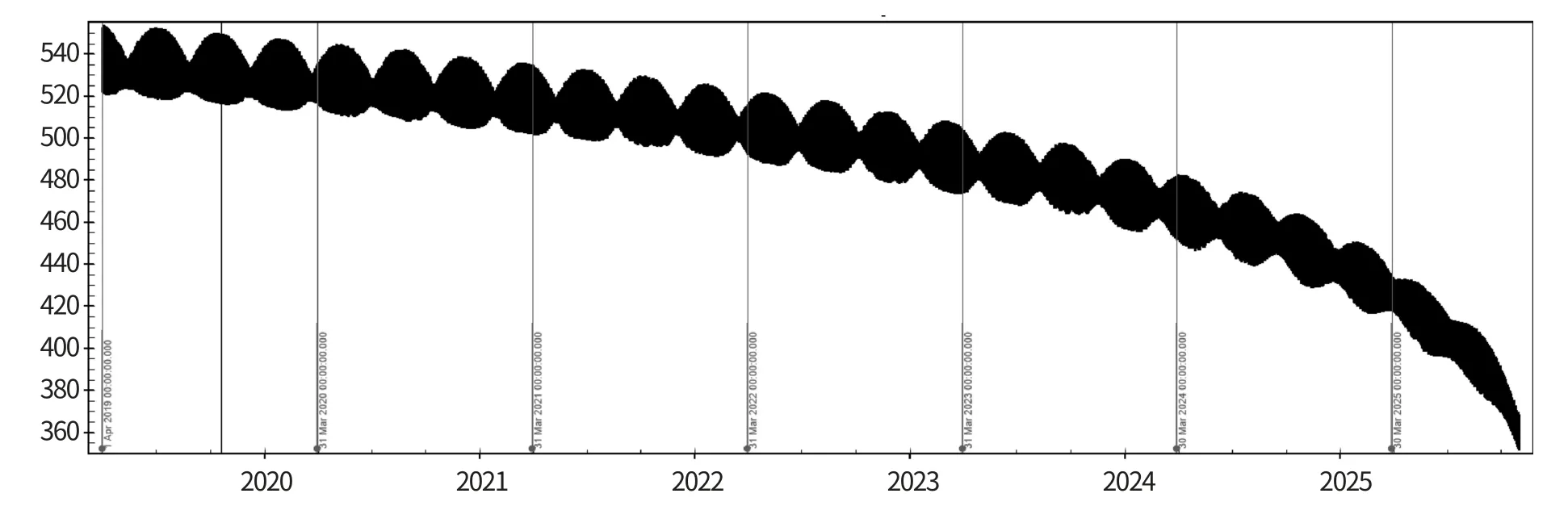
图8 离轨帆展开后轨道高度演化Fig.8 Evolution of orbital altitude after deploying the deorbit sail

根据2019 年11 月到2020 年2 月对天仪包括无离轨帆和有离轨帆的卫星在内的多颗卫星的轨道高度的演化过程进行统计， 结果如图7 所示，“潇湘一号03 星” 的轨道衰减速率明显高于无离轨帆的4 颗卫星， 从而也证实了离轨帆的有效性。

因HPOP 轨道模型大气参数取值不精确， 导致外推积累误差会逐渐变大， 因此， 在本文实际计算时， 这些误差的效果都通过面质比推算值反映出来， 因此得到的面质比是包含一定误差的，需要后续进一步根据实际轨道数据修正。

按此面质比推算， 陨落时间为2025 年10 月，卫星在轨时间6 年。

为进一步加快离轨速度， 2019 年11 月后， 通过指令控制卫星进入离轨模式， 即控制卫星处于-Y 轴(帆板法线方向) 指向轨道速度方向的模式， 以获取最大气动阻力， 在此期间， 根据能源情况， 需要短时间控制卫星转为帆板法向指向太阳， 进行充电后再转回。 上述过程由星上自主完成， 无需地面干预。

选取离轨模式下2020 年1 月25 日和2020 年2 月25 日的两行轨道根数， 如下:

1 月25 日两行根数见表7。

表7 1 月25 日轨道两行根数Table 7 Radical of two rows of tracks on January 25

2 月25 日两行根数见表8。

表8 2 月25 日轨道两行根数Table 8 Radical of two rows of tracks on February 25

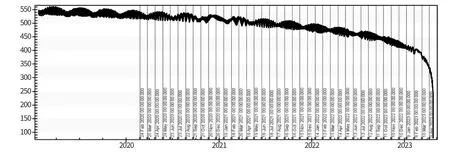
图9 卫星进入离轨模式后的轨道高度演化Fig.9 Orbital altitude evolution of the satellite after entering into the deorbit mode

根据相同的方法， 得到平均迎风面积为0.52m2， 面质比为0.067m2/kg。

进一步推算， 陨落时间大约为2023 年4 月，卫星在轨寿命为4 年。

需要说明的是， 表征太阳活动强度的F10.7的值对卫星在轨寿命影响很大。 太阳活动增强，会导致地球高层大气的气体分子活动加剧， 从而对卫星的阻力加大， 陨落速度加快。 而F10.7 的年度变化有明显的周期特性， 在平静期F10.7 在100 以下， 太阳活动剧烈时F10.7 可以达到200以上。 如图10 所示。

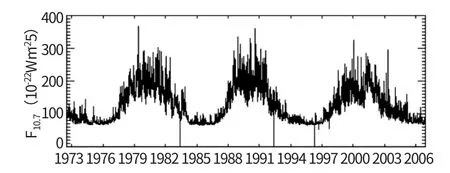
图10 太阳辐射指数F10.7 年度变化情况Fig.10 Changes of solar radiation index F10.7

查询数据可知， 当前太阳处于平静期， F10.7低年。 而按照太阳11 年活动周期， 大约在2023 年会再次达到高年。 如果按F10.7 =120 的高年平均值推算， 陨落时间将缩短至1 年左右。

6 结论

采用增阻离轨帆作为低轨小卫星的寿命末期离轨手段， 结构重量小， 工作可靠， 离轨效果好。 在同样的轨道模型参数下， 安装离轨帆与不安装离轨帆相比， 离轨时间由16 年缩短为6年(磁控自旋模式) 或4 年(离轨模式)， 是一种很有前途的离轨方式， 可在后续卫星设计和应用中推广。