基于华东地区航空货运运力均衡性的定价策略研究

沈嘉一 肖恢翚 俞一帆 卢从亦 顾一鸣

摘 要：本文以市场角度，充分考虑供需与运价关系，在华东地区航空货运运力均衡前提下，尝试建立差别定价模型和动态定价模型，研究这两个定价策略是否可以给航空公司带来利润最大化。确定在供需均衡情况下航空货运最优定价策略，给我国华东地区航空货运企业提供借鉴和策略。

关键词：华东地区;航空货运;运力均衡;货运定价

1研究背景及意义

如今，我国进出口贸易不断扩大，航空货运的发展将会为其提供更加广阔的机会和市场空间。所以，在这一特定市场中，航运运力资源性配置和均衡性极为关键，如何使航空货运利益达到最大化则与相关的定价策略密不可分。研究华东地区航空货运运力均衡性的定价策略，可以对航运市场做出灵敏反应，对于日益变化的市场来说，可使航空公司做出有效调整，提升资源有效使用，不仅可以刺激市场，推动我国航空货运业的发展，并且带动当地区域的经济发展。

2航空货运定价体系及定价模型构建

2.1基于市场细分的差别定价模型构建

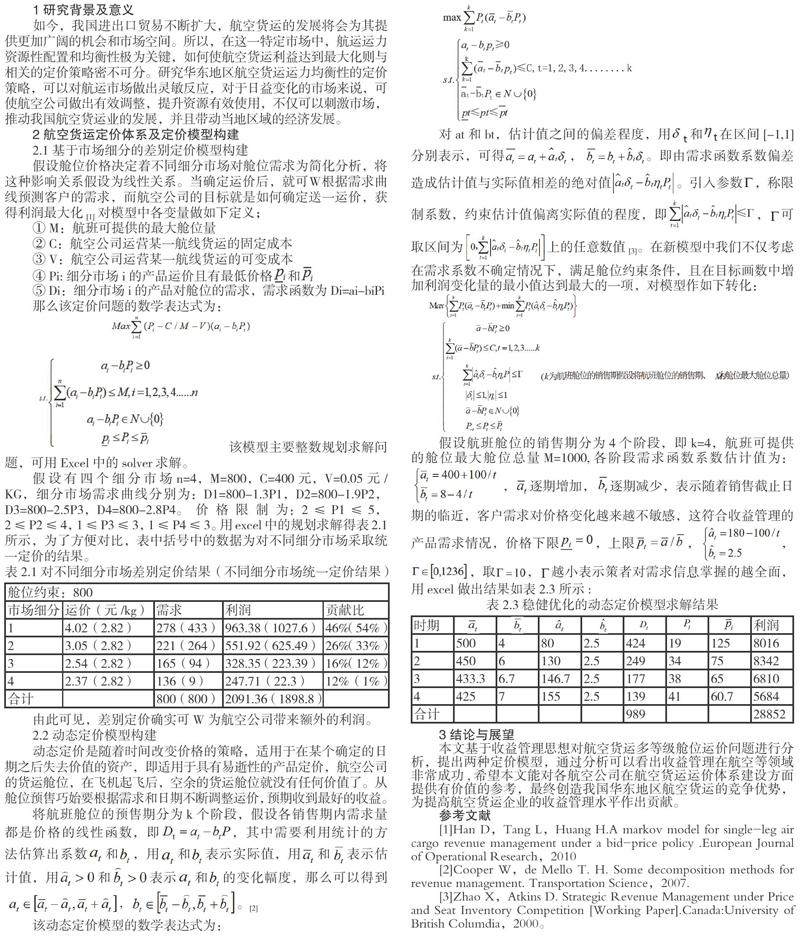
假设舱位价格决定着不同细分市场对舱位需求为简化分析，将这种影响关系假设为线性关系。当确定运价后，就可W根据需求曲线预测客户的需求，而航空公司的目标就是如何确定送一运价，获得利润最大化[1]对模型中各变量做如下定义;

①M：航班可提供的最大舱位量

②C：航空公司运营某一航线货运的固定成本

③V：航空公司运营某一航线货运的可变成本

④Pi：细分市场i的产品运价且有最低价格和

⑤Di：细分市场i的产品对舱位的需求，需求函数为Di=ai-biPi

那么该定价问题的数学表达式为：

该模型主要整数规划求解问题，可用Excel中的solver求解。

假设有四个细分市场n=4，M=800，C=400元，V=0.05元/KG，细分市场需求曲线分别为：D1=800-1.3P1，D2=800-1.9P2，D3=800-2.5P3，D4=800-2.8P4。价格限制为：2≤P1≤5，2≤P2≤4，1≤P3≤3，1≤P4≤3。用excel中的规划求解得表2.1所示，为了方便对比，表中括号中的数据为对不同细分市场采取统一定价的结果。

由此可见，差别定价确实可W为航空公司带来额外的利润。

2.2动态定价模型构建

动态定价是随着时间改变价格的策略，适用于在某个确定的日期之后失去价值的资产，即适用于具有易逝性的产品定价，航空公司的货运舱位，在飞机起飞后，空余的货运舱位就没有任何价值了。从舱位预售巧始要根据需求和日期不断调整运价，预期收到最好的收益。

将航班舱位的预售期分为k个阶段，假设各销售期内需求量都是价格的线性函数，即，其中需要利用统计的方法估算出系数和，用和表示实际值，用和表示估计值，用和表示和的变化幅度，那么可以得到。[2]

该动态定价模型的数学表达式为：

对at和bt，估计值之间的偏差程度，用和在區间[-1，1]分别表示，可得，。即由需求函数系数偏差造成估计值与实际值相差的绝对值。引入参数，称限制系数，约束估计值偏离实际值的程度，即，可取区间为上的任意数值[3]。在新模型中我们不仅考虑在需求系数不确定情况下，满足舱位约束条件，且在目标画数中増加利润变化量的最小值达到最大的一项，对模型作如下转化：

3结论与展望

本文基于收益管理思想对航空货运多等级舱位运价问题进行分析，提出两种定价模型，通过分析可以看出收益管理在航空等领域非常成功，希望本文能对各航空公司在航空货运运价体系建设方面提供有价值的参考，最终创造我国华东地区航空货运的竞争优势，为提高航空货运企业的收益管理水平作出贡献。

参考文献

[1]Han D，Tang L，Huang H.A markov model for single-leg air cargo revenue management under a bid-price policy .European Journal of Operational Research，2010

[2]Cooper W，de Mello T. H. Some decomposition methods for revenue management. Transportation Science，2007.

[3]Zhao X，Atkins D. Strategic Revenue Management under Price and Seat Inventory Competition [Working Paper].Canada：University of British Columdia，2000。