浅谈整体视角下分数概念教学
周晓婷
数学概念是客观现实中的数量关系和空间形式的本质属性在人脑中的反映。分数概念内涵丰富,抽象性高,是小学阶段极其重要的概念。因此,人教版教材分两个阶段:三年级认识“一个物体”的几分之几,五年级认识“一些物体”的几分之几。从教材来看,实现了概念的逐层递进、螺旋上升,但在教学中,常常囿于教材内容与课时目标进行节点性教学,容易导致分数概念理解的短视与偏差。笔者认为,只有从整体视角下去解读教材,分解概念认识的阶段,才能让学生更全面、更深入地掌握概念的本质。
整体解读教材,统筹规划教学
把握结构,准确定位 现行的数学教材是按数学知识的逻辑结构,螺旋上升编排的。知识的多次再现,相互沟通内在联系,使学生对所学的知识有更深刻的理解。因此,教师在教学新知前,要有瞻前顾后的意识,明确新知在整个知识体系中的位置与作用,教学时才能做到有的放矢。
人教版教材小学阶段的分数概念分为两个认识阶段。第一个认识阶段安排在三年级,进行分数的初步认识,是一个物体与部分的关系。也就是把一个物体看作单位“1”,把一个物体平均分成几份,其中一份是这个物体的几分之一,一个物体也就是一个具体意义上的单位“1”的概念。这一阶段的教学定位,必须让学生在实际操作活动的过程中,了解分数形成的过程,理解分数表示的是一个物体与部分的关系,从而初步理解分数的概念。第二个认识阶段安排在五年级,进行分数的再认识,是一个整体与部分的关系。也就是把多个物体看作一个抽象整体,把这个抽象整体平均分成几份,其中一份是这个抽象整体的几分之一,一个整体就是一个抽象意义上的单位“1”的概念。这一阶段的教学定位,在分数初步认识的基础上,理解多个物体组成的整体与部分之间的关系也能用分数表示,丰富单位“1”的内涵,全面地理解分数的意义。
区别对待,有效实施 分数概念的教学是从初步认识到再认识的合理安排和循环递进,由于一个物体的分数认识与一个整体的分数认识具有结构类同的关系存在,应以一个物体的分数认识为教学结构阶段,以一个整体的分数认识为运用结构阶段。
一个物体的分数认识教学结构阶段,教师可从1/2这个分数着手,提供给学生一些丰富材料(包括現实材料和几何图形材料)表示分数。教师要引导学生对表示情况进行不同标准的分类,深刻地理解二分之一的意义。接着让学生认识几分之一、几分之几,最后总结一个物体的分数意义。让学生经历“辨析比较,理解二分之一——拓展分数,抽取本质——归纳概括,总结概念”的分数概念形成过程。在最后的练习阶段,加入“以几当一或以一当几”的材料,加深意义理解,把握概念本质。
一个整体的分数认识运用阶段,可以让学生运用这样的过程结构主动建构一个整体的分数认识。教师可以让学生在多个物体的材料中表示分数,利用学生对一个物体分数的认识,展示多样化的分法,体验在一个整体中表示分数,然后与一个整体的分数认识进行比较,找出异同点,理解分数意义。过程中,不仅可以培养学生材料处理和辨析比较的能力,还可以培养学生形成发现相同材料中隐藏着各自不同特点的数学眼光,更可以培养学生透过表面现象发现本质属性的抽象能力,从而理解分数意义。
找准关键点,适时前伸后延
数学学习具有累积性,后一阶段的学习是建立在学生已有知识和经验的基础上的,是对前一阶段知识与经验的的深化与发展。教学时要根据知识的前后联系,纵横发展来找准知识的关键点,为使学生的后续有较大的发展。
着力连接点 真正建立分数概念,需要学生学习一个物体的几分之一时,从“几分之一个”抽象到“它的几分之一”,初步体会分数表示关系的内涵。学习多个物体组成的一个整体的几分之一时,需要激活这些经验以同化新知。教学中应找准两个阶段学习中同化知识的关键点,即突出“几份中的一份”这一本质关系,逐步舍弃“物体的个数”这一非本质属性,分数表示的是平均分的份数与取的份数,也就是整体与部分的关系。
在认识分数的第一阶段,通过变式练习进行后延,让学生逐步舍弃“以一当一”的想法,真正从单个整体平均分的份数和取的份数体会分数是表示关系的,为多个物体表示分数奠定基础。如题组:涂色分别表示两个长方形的3/7(一个长方形平均分成了14份、一个长方形平均分成7份),让学生体会分数是和平均分的份数和取的份数有关,和每份的个数是无关的。
在认识分数的第二阶段,充分利用学生对分数已有的知识基础自主建构学习。知识的前伸,使单位“1”自然从一个物体过渡到一个整体,突破教学难点。先用不同平均分的方法表示出不同的分数。然后把16个小正方形动态散开,并把它们看成一个整体(画上一个集合圈),再请学生平均分一分,表示出一个分数。(如下图1),最后把前后两张图所表示出的分数进行异同比较,概括出分数的概念。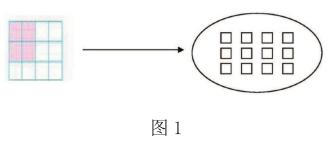
与此同时,我们发现教材中呈现的平均分素材,总是从左往右或从上往下进行平均分,这样编排往往给学生带来了负面的认知影响,对概念认识产生认知偏差。接着出现下图2,许多学生都认为这不可以用分数来表示。他们认为没有平均分怎么能用分数表示呢?通过电脑演示,将右侧三个小正方体旋转平放在最上面,学生看到此图后立刻明白,可以用分数表示。经过这样的学习过程,剔除了一些对概念认知的无关干扰,凸显了平均分的本质。通过科学且全面的素材,并用多样化的方式呈现出来,才能使得概念的意象更丰盈,学生更为深刻地把握概念本质。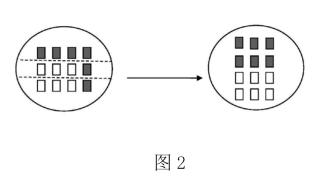
关注教学过程,注重概念解读
概念是通过分析和综合、求同和求异、抽象和概括等一系列的思维活动形成的。有时学生在接受数学概念时,由于操作形式化、提问肤浅化、素材单一化,造成学生只是鹦鹉学舌地说某个分数的意义,而并非是基于自己的理解。教学中应注意以下三个方面:
改变操作顺序,经历概念形成 通过不同材料表示出1/2的操作,再抽象出二分之一的意义。这样操作的本质是为抽象的分数寻找一个具体的表象,对学生来说思维顺序是反的,我们必须让学生经历概念形成的过程。因此在第一阶段教学中,抓住1/2这个分数重点认识,可以先让学生把各种材料分成2份,表示1份,然后把材料按是否平均分分类,从平均分这类中概括共性,接着说说1/2的意义,最后从生活中找1/2的原型,进一步理解1/2的意义。
改变提问方式,帮助概念建立 在思维的转折处和关键处设问,能够引导学生研究、讨论,积极思维,才能使学生深刻理解概念的内涵,抓住本质特征。在第二阶段教学中,要让学生更多地说自己抽象出分数的过程,减少关注结果的提问。如:“你是如何表示这幅图的1/4的?”这样的提问方式和教材上的练习材料是同质的,关注的都是结果。教师可以这样问:“为什么不同的图都可以用1/4来表示?”“要知道这个图表示几分之几,需要哪几个条件?”总之提问的方式应更多关注意义的本身和学生的思维过程,而不是答案。
改变素材呈现,促进概念理解 数学概念的学习过程包括概念的应用,这就需要学生在初步理解概念的基础上,利用多样化的素材,运用习得的知识解决相应的问题,使概念得以巩固和内化,从而更深对概念的理解。
第一阶段分数的初步认识教学中,不仅要把分数与几何图形建立联系,更要注意与生活联系,拓展学生的视野和思维,使学生对概念的内涵有充分的认识和体验。如1瓶果汁平均分给5个小朋友的關系,1个吊扇与3片叶片的关系,1扇窗子与其中4块玻璃的关系等等。
第二阶段分数意义教学中,不能仅仅停留具体情境下对分数意义的诠释,更应为学生后续有关分数的学习作好铺垫。如借助小棒进行如下活动。
活动1:看小棒(四行三列)写分数。引导思考“你看出分数来了吗”,让学生写出相等的不同分数,讨论“你是怎样想的”“这些分数都是正确的,它们的意义一样不一样”,进一步加深分数的理解;
活动2:按老师的要求分别拿出12根小棒的1/3、1/()、()/6,通过“分母没有出来的时候,能拿吗?”“分母是6,我们可以做什么?”等问题,让学生进一步理解分母、分子所表示含义,促进对意义的理解;
活动3:拿另一捆小棒的1/4,由于学生手中的小棒根数是不同,拿出的根数也不同,请学生寻找原因。让学生理解“一个整体”的变化,不同的数量可以用同一个分数表示,进一步深化分数表示了整体与部分的关系,与每份的数量无关。
数学特级教师俞正强说:“当学生的数学学习发生困难时,回到源头去。一定是在某个时候,我们曾经省略了一段阳光。” 这段被省略的“阳光”,应该就是知识的“序”与学生认知的“序”之间的连接点。作为教师用长程的整体视角去解读概念认知的结构,建立教学整体性观念,打通节点性课堂教学与整体性知识脉络联系,实现概念内涵的深入化,概念外延的有向放大化。
(作者单位:浙江省杭州市半山实验小学)

