基于Contourlet变换阈值选取的算法研究
王伟兵 杨铮 霍迎科 李仁华


摘 要:针对CT图像在生成或传输时容易受到噪声影响这一难题,提出了基于Contourlet变换结合PCA阈值的去噪方法。 首先,对噪声图像进行Contourlet变换。然后,对DFB方向滤波后得到的Contourlet系数进行PCA阈值及硬阈值函数去噪。最后,对去噪后的Contourlet系数进行Contourlet逆变换,得到去噪图像。通过对图像添加噪声并与Contourlet结合六种不同阈值去噪方法进行对比,采用PSNR评估去噪优劣。结果表明:贝叶斯阈值方法PSNR值最高PSNR=94.88 dB,然后是PCA阈值PSNR=83.02 dB,最后依次是配套改进阈值PSNR=73.97 dB、3σ阈值PSNR=73.27 dB、统一阈值PSNR=72.33 dB、通用阈值PSNR=71.50 dB。PCA阈值去噪结果整体平滑性较好,视觉效果较好;贝叶斯阈值去噪结果整体平滑性较差,视觉效果不佳。通过将Contourlet 变换框架取代传统小波变换框架并结合PCA 阈值应用在图像去噪中,不仅信噪比有所提高,而且图像视觉效果也明显改善。
关键词:CT图像;去噪;Contourlet;Wavelet;PCA;閾值
中图分类号:TP391 文献标识码:A
Research on Threshold Selection Based on Contourlet Transform
WANG Wei-bing,YANG Zheng?,HUO Ying-ke,LI Ren-hua
(Automation Department Handan Iron and Steel,Handan,Hebei 056000,China)
Abstract:In view of the influence of noise on the generation of CT images. A de-noising method based on Contourlet and PCA for images is proposed. Firstly,Contourlet transform is applied to noisy images. Then,the Contourlet coefficients obtained after filtering in DFB direction are threshed to denoise by PCA. Finally,PCA inverse,Contourlet inverse transformation of the Contourlet coefficients after denoising is performed to get the denoised image. By adding noise to images and comparing with Wavelet combined with Contourlet wavelet six de-noising methods are compared and PSNR is used to evaluate the advantages and disadvantages of de-noising. The results show that Bayes threshold method obtains the highest PSNR = 94.88 dB,Then,the PCA threshold PSNR = 83.02 dB,Finally,the matching improved threshold PSNR = 73.97 dB,3σ PSNR = 73.27 dB,Donoho& Johnstone threshold PSNR = 72.33 dB,and universal threshold PSNR = 71.50 dB. PCA threshold denoising results have higher smoothness and better visual effect;Bayes threshold denoising results have worse smoothness and poor visual effect. By replacing the traditional wavelet transform frame with the Contourlet transform frame and applying it to image denoising with PCA threshold,not only the signal-to-noise ratio is improved,but also the image visual effect is improved obviously.
Key words:CT images;de-noising;Contourlet;Wavelet;PCA;threshold
计算机断层扫描(CT,computed tomography)成像是当下广泛应用的影像技术,在临床诊断和研究中显得极为重要[1]。CT技术具有多功能、多参数、多平面成像、高空间分辨力、高密度分辨力等优点[2]。但是在CT扫描获取图像过程中受到外界噪声干扰,从而造成图像局部区域模糊的现象,这对医疗人员在对CT图像的分析时带来不便,分析不当会对患者造成危害。因此,对CT图像进行去除噪声研究具有重要的临床指导意义。噪声会把CT图像中的局部信息覆盖,而覆盖部分信息很有可能隐藏着重要信息。图像去噪目的就是要从被噪声污染的含噪图像中提取出原始图像。传统小波变换去噪方法,在对医学图像去噪效果上取得不错的效果,但是,因小波方向性不足,对于更高要求的来保留图像细节部分来讲,小波变换去噪方法不能满足,为了解决小波变换去噪算法的不足之处,提出了基于Contourlet变换的阈值去噪研究[3]。
为了能够使Contourlet变换能得到更好地去噪效果并且可以准确捕获图像中占比例大的边缘信息。该研究在Contourlet变换的阈值选取部分做了替换研究,把文献[11]《基于Contourlet变换在图像去噪中的应用》的第47页中Donoho & Johnstone提出的统一阈值被替换为PCA阈值(Principal Component Analysis,PCA),PCA可以理解为一种统计分析方法,将原来多维指标信息重新组合成一组相互独立的低维指标信息,这些低维指标信息可以尽可能地反映原来多维指标信息,从数学角度上来看,PCA技术其实是一种数据降维处理。
通过实验结果证明该方法可达到较好的信噪分离[4]。充分利用Contourlet变换良好的稀疏特性和PCA在高维数据处理中的高效性及一定的噪声消除能力,不仅能够更好地消除噪声,而且能够较好地恢复原始图像信息。
1 分析方法
1.1 Contourlet变换
Contourlet变换是首先使用拉普拉斯金字塔LP(Laplacian Pyramid,LP)对图像进行多尺度分解,LP分解是用来捕捉点奇异,然后使用方向滤波器DFB(Directional Filter Bank,DFB)组将同一方向上的奇异点合并成一个系数。Contourlet变换结果是用类似线段的基的结构来描述原始图像[5-6]。Contourlet 变换是一种“合适”的 2 维图像稀疏表达方法,Contourlet 变换不但具有小波变换的多分辨率时频分析特征,还具有比小波变换更丰富的方向分量,能更稀疏地表示原始图像。
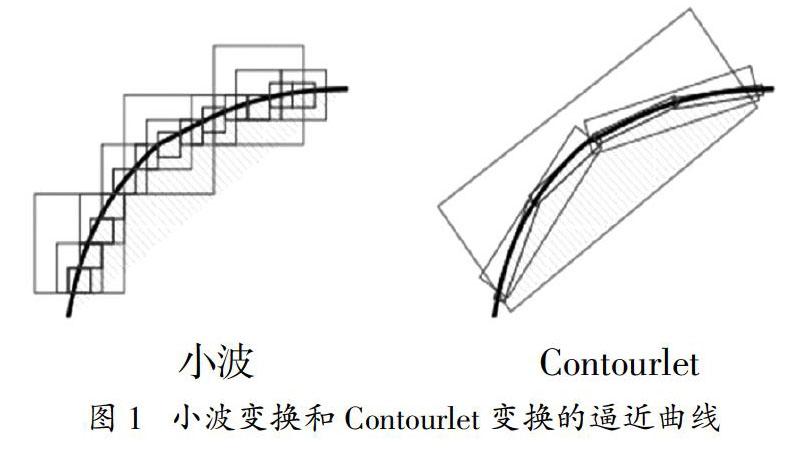
图1给出了小波变换和 Contourlet 变换的逼近曲线,可以看出 Contourlet 基的支撑区间具有随尺度而长宽比变化的“长方形”结构,而小波变换是“正方形”结构,因此,Contourlet 变换具有良好的各向异性,可以沿着图像轮廓边缘使用最少的系数来逼近奇异曲线,实现用“稀疏”表示原始图像[7-8]。
Contourlet 变换的基本思想是先用一个类似小波的多尺度分解捕捉边缘奇异点,再根据方向信息将位置相近的奇异点汇集成轮廓段。即先选用拉普拉斯塔式滤波器结构 LP 对图像逐步滤波得到图像的多分辨率分解。然后,对 LP 分解得到的每一级高频分量再使用二维方向滤波器组DFB进行方向性分析,这样,在任意尺度上可分解得到2n次方数目的方向子带[9-10]。
图 2 给出了 Contourlet 变换对图像进行分解的过程。可见Contourlet 变换可以进行多分辨率、多方向性的变换,它允许在每个尺度上有不同数目的方向子带。由于 Contourlet 变换良好的图像稀疏性表示和非线性逼近性能,使得其在图像的分析和处理中得到了成功的应用。
1.2 统一阈值法
Donoho & Johnstone提出的统一阈值是在标准正态高斯噪声情况下,针对彼此间相互独立的正态随机变量的联合分布,在维数趋于无穷时得出的结论,即大于该阈值的系数是噪声的概率趋于零。但当MN较大时,也会变得很大,所以在这种情况下,统一阈值对图像信号系数有“过扼杀”的倾向。它仅考虑了噪声的特性,并没有考虑图像信号本身。因此,该阈值是最佳阈值的上限值,而不是最佳阈值。统一阈值[11]:
式中:σ是噪声标准差估计值,MN是脑部CT图像的尺寸。
1.3 PCA阈值法
由于噪声频谱主要集中在高频部分,经过Contourlet变换分解后噪声主要在高频细节系数中,将各高频子带做了分块处理(每个子块为K × N的区域)。在每个Contourlet域子块内,将每行小波系数看作N维行向量Xi,则有K个行向量组成K × N矩阵X[12]:
协方差矩阵Cx的N个特征值按照递减顺序排列λ1 ≥ λa ≥ … ≥ λN,其对应特征向量u1、u2、…、uN构成特征空间的一组基。其中前d(< 按(4)式完成对K个行向量的重建,得到原X的重建矩阵[X][^]。其绝对值的均值可以作为对该子块内由噪声引起系数幅值的估计[λ][^],即[λ][^]为阈值处理,代替了传统统一阈值[14]: 1.4 Contourlet的PCA阈值法去噪 该研究思想来源借鉴于基于小波變换的阈值去噪算法,基于Contourlet变换的阈值去噪算法首先假设Contourlet系数间的相互独立性,然后参照小波变换的阈值去噪算法的流程对系数进行处理(图3),最后调试并生成去噪算法。由于Contourlet变换较小波变换而言,Contourlet变换去相关能力要强,在Contourlet域里,噪声与图像的Contourlet系数将更容易分离。因此,在Contourlet变换的基础上采用基于阈值的去噪算法,也将能取得比较理想的去噪效果。 Contourlet 变换将多尺度分析和方向分析分开进行。首先用拉普拉斯金字塔变换LP进行多尺度分析捕捉奇异点。然后用方向性滤波器组DFB将分布在同一方向上奇异点合成为一个系数,捕捉高频分量。最后用PCA阈值及硬阈值函数处理高频分量系数并完成DFB重构和LP重构。 基于Contourlet的PCA阈值结合硬阈值函数的去噪流程图和具体步骤如下: (1)对噪声图进行Contourlet变换。对噪声图进行拉普拉斯金字塔分解(LP),得到图的低频与高频部分。对图高频部分进行方形滤波器组(DFB)方向滤波,得到Contourlet系数。 (2) 对Contourlet系数进行PCA阈值、阈值函数(硬阈值函数)对Contourlet系数与进行去噪处理,得到去噪后Contourlet系数。 (3)对去噪后的Contourlet系数进行Contourlet逆变换。对逆变换后的Contourlet系数进行DFB重构,合成去噪图的高频部分。 (4) 对原噪图的低频部分与去噪图的高频部分进行LP重构,合成去噪图。 1.5 去噪评价指标 实验采用峰值信噪比(PSNR)作为评价图像优劣指标,PSNR是计算原始图像与去噪图像之间的相似度。该研究采用PSNR的表达式如下[15]: 其中:I0、I分别为原始图像、去噪图像各点灰度值,L、W表示图像长、宽。PSNR越大,去噪图像与原始图像之间的相似度就会越高,则说明去噪图像失真越小,视觉效果越好。 2 实验结果 本次实验对象为医学脑部CT(512 × 512)图像,如图4所示。图5是对图4添加噪声标准差σ = 0.05的噪声的图像。 方向滤波器(DFB):“pkva”,拉普拉斯金字塔滤波器(LP):“9 - 7”双正交小波,分解结构参数:[0,0,4,4,5]。阈值:图6的PCA阈值和图7的统一阈值,阈值函数:硬阈值函数。图6是对图7在阈值设定上做了进一步改进研究,将统一阈值替换为PCA阈值。图6的降噪效果PSNR = 83.02 dB。图7的降噪效果PSNR = 72.33 dB。从图6和图7的结果中可以看出,该研究提出的基于Contourlet的PCA阈值结合硬阈值函数去噪算法在降低噪声的同时,有效的保留了CT图像的纹理和细节特征,而基于Contourlet的统一阈值结合硬阈值函数的去噪算法仍旧残留了较多的噪声信息。 阈值设定是图像去噪过程中非常关键的环节。如果阈值选取过大,则图像部分有用信号会被视为噪声滤除出去;如果阈值选取过小,则噪声部分无用信号会被视为图像信号系数被保留下来。传统阈值除了统一阈值外,还包括3σ阈值[16]、贝叶斯阈值[17-18]、最大最小阈值、SURE Shrink阈值[19]、GCV阈值[20]、通用阈值、Neigh Shrink阈值[21]、M.N.Do & Martin Vetterli阈值[22](文献[22]《基于阈值的 Contourlet 变换图像去噪算法》的第32页一文中Donoho & Johnstone提出的专门为 Contourlet 变换所配套的一种改进阈值)。在这里给出基于 Contourlet的配套改进阈值、3σ阈值结合硬阈值函数的去噪算法。目的是进一步验证基于 Contourlet 的PCA阈值结合硬阈值函数的去噪算法的有效性。 其中,3σ阈值计算方法为:[λ][^] = 3σ。3σ阈值设立的原理为“准则”,及零均值高斯分布随机变量落在[-3σ,3σ]之外的概率非常小,因此绝对值大于3σ阈值的变换系数一般被认为是图像信号系数,而小于3σ的变换系数是噪声系数的可能性非常大。配套改进阈值计算方法为:首先确定基本阈值和噪声在contourlet域的标准差σ。然后计算改进阈值[λ][^] = [λ][^] × σ。最后调整底层精细尺度系数阈值[λ][^] = [λ][^] × 4/3。 图8为基于Contourlet的3σ阈值结合硬阈值函数的去噪效果图。图9为基于Contourlet的配套改进阈值结合硬阈值函数的去噪效果图。 图8的降噪效果PSNR = 73.27 dB。图9的降噪效果PSNR = 73.97 dB。从图6 ~ 图9的结果中可以看出,基于Contourlet的PCA阈值结合硬阈值函数去噪算法去噪效果相对于基于Contourlet的配套改进阈值、统一阈值、 3σ阈值结合硬阈值函数的去噪算法较好。 在这里给出在研究阈值选取过程中遇到基于Contourlet的贝叶斯阈值结合硬阈值函数去噪算法的去噪效果比基于 Contourlet 的PCA阈值结合硬阈值函数去噪算法好。图10为基于 Contourlet 的贝叶斯阈值结合硬阈值函数的去噪效果图。图10的降噪效果PSNR = 94.88。 假设变换系数服从广义高斯分布,那么它的Bayes Shrink阈值计算方法为:[λ][^] = σ2/σβ。其中,σ为噪声标准差,σβ为原图像的标准差[23]。Bayes Shrink阈值是由Chang & Vetterli根据图像变换系数分布的特点,提出了一种基于Bayes准则的图像去噪方法[24]。 图11为基于Contourlet的通用阈值结合硬阈值函数的去噪效果图。图11的降噪效果PSNR = 71.50 dB。通用阈值是不带有噪声估计,通用阈值计算方法为[λ][^] = 。 表1给出了结果与讨论中为该研究的不同阈值选取去噪方法的CT图像去噪效果对比。六种阈值去噪算法的去噪效果優劣顺序可排列为:贝叶斯阈值 > PCA阈值 > 配套改进阈值 >3σ阈值 > 统一阈值> 通用阈值。此外,随着噪声强度(σ)的增加,六种阈值去噪方法的去噪效果(PSNR)均存在减小的趋势,造成该现象的原因是噪声密度变大,含噪图像与原始图像之间的差异变大,增加了图像去噪的难度[25]。 3 讨 论 六种阈值去噪方法的图像去噪效果对比。从去噪效果上看,基于Contourlet的贝叶斯阈值结合硬阈值函数的去噪方法的去噪效果最好,其次是基于Contourlet的PCA阈值结合硬阈值函数的去噪方法。再者是基于Contourlet的配套改进阈值结合硬阈值函数的去噪方法。然后是基于Contourlet的统一阈值结合硬阈值函数的去噪方法。最后是基于Contourlet的通用阈值结合硬阈值函数的去噪方法。理论上PSNR值越大,则表示失真越少,视觉效果越好,图像画质越好。阈值选取不同,则去噪效果不同。 將图10与图6进行对比分析可以看出,虽然基于Contourlet的PCA阈值结合硬阈值函数的去噪方法的去噪效果不如基于Contourlet的贝叶斯阈值结合硬阈值函数的去噪方法。但是基于Contourlet的PCA阈值结合硬阈值函数的去噪方法的结果具有整体平滑性(光斑较少不模糊),其本质原因与阈值本身有关,阈值形式不同,则去噪原理不同。也极有可能某些阈值只是对一种或者几种特定的图像信号去噪效果较好。 该研究选择的是硬阈值函数结合PCA阈值进行降噪,也可以从其他阈值函数角度考虑。比如软阈值函数、半软阈值函数、改进阈值函数,改进阈值函数设计可以根据函数渐进性、无偏差性连续性、三个性质[26-27]。满足上述三个性质仅是理论,需要验证改进后的小波阈值函数的去噪效果是否优于传统阈值函数。其实,改进阈值函数是针对传统小波软阈值函数和硬阈值函数以及半软阈值函数的不足而提出的一种函数,该改进阈值函数需要克服硬阈值函数的不连续性和软阈值函数的偏差性缺点以及半软阈值不连续性和偏差性。不同阈值函数在信号上去噪效果不同,这和函数本身有着必然的联系。基于Contourlet的阈值去噪方法在阈值函数选取上拥有很大的可提升空间。 4 结 论 Contourlet变换是一种新的多尺度几何分析方法,不但有着小波变换的多分辨和时频局部化的特性,而且还具有多方向特性及各项异性特性。Contourlet变换实现了对图像信号的稀疏表示,对分段光滑函数能够达到最优逼近,因此Contourlet变换能够更加有效地表示图像。对Contourlet变换的构造方法及实现的基本步骤进行了描述,取得良好的降噪效果。 目前,图像去噪方法基本上都是基于小波去噪方法,而小波去噪方法大多数是基于对噪声方差估计,噪声方差估计的精确性难以把握。因此利用基于 PCA 统计学特征提取方法,通过对 Contourlet 域由噪声引起的系数的能量分布进行特征提取,直接对由噪声引起的 Contourlet 系数的幅值估计,进行去噪处理。通过将PCA 阈值应用在图像去噪中,不仅信噪比有所提高,而且图像视觉效果也明显改善。 参考文献 [1] RUIKAR S D,DOYE D D. Image denoising using principal component analysis and wavelet[J]. Digital Image Processing,2012,4(5). [2] 王国树,吕发金,周 旸,等. 非线性融合技术在头颈部CTA中的价值:体模实验[J]. 中国医学影像技术,2018(7). [3] 才 溪,赵 巍. Contourlet变换低通滤波器对图像融合算法影响的讨论[J]. 自动化学报,2009,35(3):258-266. [4] 董建华,王国胤,雍 熙,等. 基于Spark的标准化PCA算法[J]. 郑州大学学报(工学版),2017,38(5):7-12. [5] 常威威,郭 雷,刘 坤,等. 基于Contourlet变换和主成分分析的高光谱数据噪声消除方法. 电子与信息学报[J],2009,31(12):2892-2896. [6] SHAH V P,YOUNAN N H,KING R. Pan-sharpening via the contourlet transform[C]// Geoscience and Remote Sensing Symposium,2007. IGARSS 2007. IEEE International. IEEE,2008:310-313. [7] 雷洁,王建成,崔清斌,等. 火炮内膛全景图像增强方法研究[J]. 计算技术与自动化,2013,32(2):142-144. [8] 曹广华,高杰,侯岩,等. 基于相关性阈值的NSCT图像去噪方法研究[J]. 计算技术与自动化,2014,33(2):93-96. [9] ZHANG S,MOLONEY C. The nonredundant contourlet transform (NRCT):a multiresolution and multidirection image representation[J]. Electrical and Computer Engineering,2008:001323-001326. [10] 王建波. 基于非下采样Contourlet变换图像多尺度边缘检测相关技术研究[D]. 郑州大学,2015. [11] 李万臣,赵开伟,陈宇贤. 基于Contourlet变换在图像去噪中的应用[J]. 仪器仪表用户,2010,17(1):47-48. [12] 宋海峰,陈广胜,杨巍巍. 基于PCA的高光谱遥感图像分类[J]. 测绘工程,2017,26(12):17-20. [13] 张久文,李建征,孟令锋. 基于Contourlet的图像 PCA去噪方法[J]. 计算机工程与应用,2007,43(21):46-48. [14] 刘帅奇. 基于多尺度几何变换的遥感图像处理算法研究[D]. 北京交通大学,2013. [15] ALMOHAMMAD A,GHINEA G. Stego image quality and the reliability of PSNR[C]. International Conference on Image Processing Theory TOOLS and Applications. IEEE,2010:215-220. [16] 張海庄,姚 梅,雷 萍,等. 远场激光光斑图像处理方法研究[J]. 激光技术,2013,37(4):460-463. [17] XIAO F,ZHANG Y. A Comparative study on thresholding methods in wavelet-based image denoising[J]. Procedia Engineering,2011,15:3998-4003. [18] 刘盛鹏,方 勇. 基于贝叶斯估计的Contourlet域图像降噪方法[J]. 计算机工程,2007,33(18):31-33. [19] XUN Z,LI J,XING J,et al. A particle swarm optimization technique-Based parametric wavelet thresholding function for signal denoising[J]. Circuits Systems & Signal Processing,2017,36(1):247-269. [20] CHENG W,HIRAKAWA K. Minimum risk wavelet shrinkage operator for poisson image denoising[J]. IEEE Trans Image Process,2015,24(5):1660-1671. [21] HAIYANG W U,WANG H. Improved threshold for image de-noising based on neighShrink[J]. Computer Engineering & Applications,2011,47(27):203-200. [22] 杨 帆. 基于Contourlet变换的图像去噪算法研究[D].北京交通大学,2008. [23] 李 金,张 毅. 一种改进的小波域贝叶斯图像去噪方法[J]. 自动化技术与应用,2012,31(1):63-67. [24] CAO B,DU Y,XU D,et al. An improved histogram matching algorithm for the removal of striping noise in optical remote sensing imagery[J]. Optik - International Journal for Light and Electron Optics,2015,126(23):4723-4730. [25] 沈 涛. 基于视频检测的行人交通参数提取技术研究[D]. 北京交通大学,2011. [26] 陈晓曦,王延杰,刘 恋. 小波阈值去噪法的深入研究. 激光与红外,2012,42(1):105-110. [27] 江 虹,苏阳. 一种改进的小波阈值函数去噪方法. 激光与红外,2016,46(1):119-122.

