架空输电线路电热耦合的并网阈值估算研究

柳明贤 李继标 李凯

摘   要：对于通过架空输电线路与主系统相连的风电场，其系统吸收的可用风电不仅依赖于发电容量，还依赖于输电阈值。为此，研究了环境条件与功率转移极限之间的密切关系，建立了架空输电线路热平衡和输电运行的联立方程，推导了稳态稳定极限的最大传输功率，并将其表示为环境因子和线路长度的函数。进而提出了一种识别初始限制并获得相应阈值的方案。分析表明，在特定风速水平下，输电过程是决定临界值的关键因素。

关键词：架空输电线路;风电一体化;电热耦合;稳态稳定极限

中图分类号：TP399                                               文献识别码：A

Estimation of Grid-Connected Threshold for Electrothermal

Coupling of Overhead Transmission Lines

LIU Ming-xian?，LI Ji-biao，LI Kai

（Lijiang Power Supply Bureau，Yunnan Power Grid Co.，Ltd.，Lijiang，Yunnan 674100，China）

Abstract：For wind farms connected to the main system through overhead transmission lines，the available wind power absorbed by the system depends not only on the generating capacity，but also on the transmission threshold. This paper focuses on the close relationship between environmental conditions and power transfer limit，establishes a simultaneous equation of overhead transmission line thermal balance and transmission operation，derives the maximum transmission power of steady-state stability limit，and expresses it as a function of environmental factors and line length. Then a scheme is proposed to identify initial constraints and obtain corresponding thresholds. Case study shows that the transmission process is the key factor to determine the critical value at a given wind speed level.

Key words：overhead transmission lines;wind power integration;electrothermal coupling;steady-state stability limit

風力发电作为可再生能源，其良好的环境效益和经济效益而得到了广泛的发展，然而大量可开发的风能资源都位于远离负荷中心、气候条件恶劣的偏远多风地区[1]。架空输电线路（OTL）作为最经济的输电方式，可将风电场的电力安全、高效地输送到主电网[2]。随着大规模风电开发的增加，解决风电一体化（WPI）既涉及风力发电又涉及风电注入主系统[3]。考虑到风电场运行和输电线路的电热耦合效应，WPI性能不仅受环境因素的驱动，还受环境因素的限制，包括风速、环境温度等[4]。文献[5]利用实时运行的动态电热学行为研究了OTL的性能及热极限（TL）。文献[6]指出OTL由电流和太阳光加热，而热量则通过对流和辐射进行消散。文献[7]在忽略环境因素的条件下研究了OTL的风速相关性，然而研究未能准确评估WPI阈值。

建立了揭示WPI与电热耦合关系的公式，推导了特定环境条件下对稳态稳定极限（SL）的具体表达式。以不同的输电线路长度为例说明了环境变量对SL的影响，进而估算风电场并网架空输电线路电热耦合的并网阈值。利用两个案例分析说明了环境和传输距离条件对WPI的影响程度，从而证明和量化所提出的方法。

1   考虑电热耦合的风电并网计算

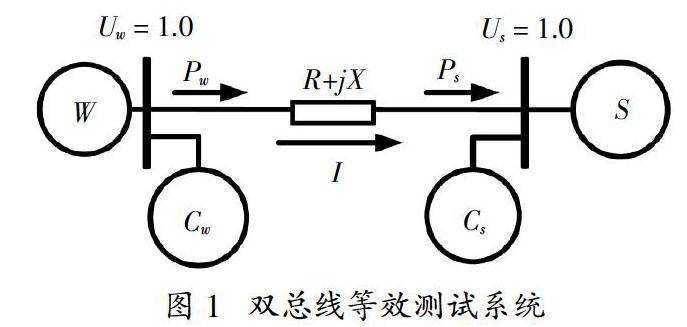
WPI的等效测试系统模型，如图1所示。其中，分别位于风电场和电力系统的两条总线通过OTL相互连接。风电通过输电线路在电源总线（总线w）和接收总线（总线s）之间传输。Uw和Us分别表示总线w和s处的电压幅值。Pw和Ps分别表示风电有功功率和系统接收的有功功率。X和R分别表示架空输电线路串联电抗和电阻。Cw和Cs分别表示总线w和s处的无功补偿。I表示导线电流。在电力系统中，各种类型的无功补偿装置用来提供最佳无功功率补偿。在这种情况下，可以假设有足够的无功电压支持在OTL的两侧产生稳定的电压幅值。

假设θ表示发送和接收总线上的复杂总线电压之间的相位角差，Ploss表示输电线路有功损耗。通过OTL传输的传输功率的标幺值可以表示为：

其中，L表示架空输电线路长度，x和r分别表示串联电抗和电阻值，ZB可根据公式（5）中的关系计算为：

其中，WPI由公式（2）定义，其表示可以集成到主系统或由主系统接收的实际风电功率[8]。假设图1中两条总线的电压幅值固定并设置为额定值，则Uw = 1.0 p.u。即所产生的风电和集成到系统中的功率的标幺值可以用公式（6）和公式（7）表示：

其中，z表示串联阻抗幅值，ZB表示相基阻抗。

假设x保持不变。此外，传输网络中的OTL通常是星型连接[9]。因此，假定相电流或导体电流等于线电流，线电流可以表示为θ、r和L的函数：

根据OTL的电热耦合算法，线路温度受两种热源的动态影响，如公式（9）所示。导体受线路电流的电功率耗散（线路欧姆损耗）发热;此外，导体温度受导体与周围环境热交换的影响较大：

其中，qc、qr和qs分别为架空输电线路的电气参数和环境变量的函数，Cp为架空导线材料的热容，Q为环境对导体热交换的影响，σ为赤纬角，T和Tl分别为导体温度和规定的导体低温，可简写为公式（10）。由于r和T之间的线性关系，如果指定了r或T中的任何一个，则可以认为另一个是已知的：

根据IEEE标准738[10]，下面给出了（10）的更详细的公式。

（1）对流热损失：qc由自然对流qcn和强制对流qcf两部分组成，具体如下：

其中，qcn仅由空气密度ρf、D和导体温度与环境温度之差Td确定，如下所示：

其中，He为导线海拔高度，Tf为边界层平均温度。

在公式（11）中，考虑风速的影响，根据公式（14）得到 qcf的值。qcfl和qcfh分别对应于低风速和高风速，其特征关系为：

此外，在公式（14）中，风向因子Ka 仅取决于风与导体轴的夹角?，如（16）所示。对于实际运行的OTL，Ka 是风向的函数，随着?的增大而增大，当? = 90°时达到最大值：

其中，文献[11]给出了不同大气为单位的太阳热强度的多项式系数，参数选择取决于OTL的实际操作条件。

由于电力系统长期运行过程中需求变化缓慢，可以假设线路温度随时间的偏差dT/dt = 0，忽略热平衡动态過程。因此，热平衡关系可以表示为：

其中，IB为基极电流，上式的左侧表示环境影响，而右侧对应于电力传输的电气性能。当给定环境参数（环境温度Ta、导线海拔高度He、架空线路导线风速Vl等）时，可通过求解公式（28）得到特定T和r的θ，然后根据公式（7）利用已知θ和r计算Ps，从而建立了WPI（Ps）、状态变量（θ，T，r）与环境参数之间的电热耦合关系。

2   稳态稳定极限（SL）

在特定的环境条件下，风力发电量和输电量的增加将导致Ps的增加，直至达到最大值Pm，这受到OTL物理特性的限制。通常，当架空输电线路的温度达到安全系统运行的最大允许温度TTL时，即可获得Ps的阈值Pm。此外，Ploss的增加可能导致T的增加，从而导致r的增加，从而进一步促进Ploss。然后，功率传输可能导致Ploss的增加大于Pw的病态状态。因此，无论风力发电量增加多少，主电力系统都无法接收更多的电力。在SL定义的临界点，T可能还未达到TTL，这使得传统的Pm计算不适用。因此，本文重点分析了SL的描述和计算方法。

2.1   临界极限的定义

复杂的环境条件，如环境温度、风速和热辐射等都可能导致SL发生较大变化，使各种稳态稳定极限下的导体温度TSL值可能低于热极限下导体最高允许温度TTL。然后，在某些情况下，单纯测试导体温度是否达到TTL所得到的Pm可能被错误估计。因此，为了确定WPI的关键限值（TL或SL），需要在特定的环境因素和一定的线路长度条件下测试 TSL和TTL之间的关系，然后计算与关键限值相对应的Pm。假设架空输电线路类型为“德雷克”导线 （795 kcmil 28毫米直径）[12]，表1给出了图1中测试系统的标幺值和具体参数。所建立的风速高、传输距离长的场景中L设置为80 km，Vl为15 m/s。

根据上文所提出的模型，Pw、Ps、I、r和T之间的关系仿真结果如图2所示。在图2（a）中，输电线路导体通过增加I来加热，这导致I和r越来越高。同时，随着I和T、Pw的增加，Ploss和Ps的变化如图2（b）所示。观察到，随着I的增加，T从原点上升到T = TSL;同时，Ps增加，直到满足以PSL表示的SL。在T > TSL的情况下，由于Ploss的上升速度快于Pw，Pw的持续上升将导致Ps的下降。在Ps的这个“拐点”，Ps对T的灵敏度为零。则临界功率定义为：

在实际系统运行中，增加输电量会使I和T逐渐升高，为保证系统安全，运行人员实时监测导线温度，确定是否需要及时调整系统运行以保证T低于TTL，相应地，如图2所示的案例研究所示，WPI将首先遇到代表SL的TSL，然后遇到与TL相对应的TTL。因为在这种情况下，随着功率传输的增加，TSL出现在TTL之前，WPI阈值Pm应该由PSL来确定，而不是由PTL来确定。然而，传统的Pm计算方法由于缺乏对SL和TSL的考虑，可能会导致错误的估计。在不失一般性的前提下，根据公式（29）中给出的关系对TTL和TSL的比较，可以判断TTL和TSL是否应该选择Pm：

当确定了OTL的物理性质和环境条件后，就可以确定Ps曲线的轮廓以及PSL和TSL的精确值。即PSL和TSL可以看作是OTL相关参数的函数。本文旨在分析PSL、L与环境参数之间的关系，其函数形式可以表示为：

其中，EP表示环境参数的集合，包括空气温度、风速、太阳辐射等。公式（31）表示的关系可用于研究特定EP下PSL和TSL的数值。虽然很难得到（31）的解析表达式，但可通过求解公式（28）计算 TSL和PSL的值。

2.2   临界极限的精确计算

通过根据上文给出的WPI公式推导公式（31）的詳细公式，从而阐明临界极限的特征。由于T和r呈线性关系，dPs /dT可以计算为：

由于qs与r不相关，则dqs /dr = 0。因此，从公式（33）到公式（41）的关系详细说明了公式（32）的表达。当给定EP和L的值时，就可以通过求解公式（32）得到TSL。由于求解了，根据公式（7）计算PSL比较容易。从而提供了计算TSL和PSL的方法。

3   参数对功率极限的影响

本节主要分析EP和L对功率限制的影响，强调了每个参数对于WPI阈值的重要性。在其它参数不变的前提下，模拟了Pm（PSL /PTL）随各参数的变化。本文中讨论的L的范围为20 ～ 140 km，参照文献[13]的TTL取值假定为100 ℃。为了获得相对适中的情况，在本节中，Vl的典型值设置为2 m/s，而其他常数与表1中的相同。

3.1   线路长度的影响

图3给出了TSL随L的显著变化。当L在20～140 km之间变化时，TSL的变化范围为584～87 ℃之间。L的增加将导致PTL、PSL和TSL下降。特别是在短距离输电线路传输（L < 107 km）时，TSL > TTL（100 ℃）和Pm=PTL。相反，对于远距离输电线路，Pm=PSL。

3.2   风速的影响

Pm和Vl之间的关系如图4所示。对于特定的L，Vl的增加将导致Pm上升。特别是对于L较长，TSL < TTL，则SL成为关键限制，对应于图4中的虚线曲线，并且Pm = PSL。因此，对于位于偏远地区的大型风电场，通常会遇到较高的风速水平，更容易遇到SL。

3.3   环境温度的影响

Ta对Pm的影响如图5所示，并且在不同的L下差异显著。此外，从图中可以看出，对于寒冷地区和远距离输电线路，SL对Pm的决定更为关键。

3.4   纬度的影响

在参照文献[14]选择的He范围内，由高度变化引起的Pm变化如图6所示，这说明He的增加可导致Pm下降。

特别是在远距离输电线路传输的情况下，SL可能成为关键因素。

4   案例研究

4.1   风速相关性处理

风速可以通过驱动风力发电机来影响WPI并且通过改变架空输电线路的热特性来影响传输性能。由于风力发电场与相邻位置的输电线路路存在密切关系，在模拟风力发电和输电运行时，还应考虑风速相关性。下面给出的假设可以为风力发电和输电的同步模拟指定相关的风速集：

（1）假设风电场及其输电线路路在相同的风速水平中。在相同高度下，风电场和OTL的平均风速相等。

（2）利用文献[15]中的指数律公式，如（42）所示，其中β设为0.2，可根据给定的参考值V（HR）推算不同高度的风速：

在50 m高（风机高度）的平均风速指定为

V（HR），架空输电线路假定为10 m高。当风速在额定值和截止值之间变化时，风力涡轮机可以运行以保持最大输出。为了分析阈值问题，本文以两个特殊点为中心的WPI性能，分别对应于风力发电的额定状态和截止状态。因此，风力涡轮机的额定风速和截止风速（12 m/s和25 m/s）相当于其架空输电线路的同步风速8.1 m/s和16m/s。

4.2   针对不同地点的解决方案

为了说明地理特征对WPI阈值的影响，以中国最南端（海口）和最北端（漠河）地区为例进行比较。相关参数如表2所示，其中Ta是根据冬季平均气温设定。OTL的其他参数与表1相同。

根据额定状态（Vl = 8.1 m/s）和截止状态（Vl = 16 m/s）规定的风速水平，该方法跟踪了PTL、PSL、TTL和TSL随L变化的解。公式（29）中给出的关系用于确定Pm的值，其等于PTL或PSL。海口市和漠河市在不同L值下的Pm结果分别如图7和图8所示。

根据额定状态或截止状态，在特定的Vl下，L的升高将导致TSL从高水平下降到低于TTL。当TSL >TTL时，对于短距离输电线路，TL有效，且SL成为长距离书输电线路（TSL < TTL）的关键约束。TSL和TTL曲线不可避免地在标记为T1和T2的点处交叉，对应于L1和L2。在交叉点附近，L的减小使得Pm = PTL，PTL由实线表示，相反，随着L的增大，PSL由虚线表示又能确定Pm。由TL或SL约束的Pm的最终结果用分段曲线表示，转折点标记为P1和P2。结果表明，Pm的轨迹随着L的增加而减小，并且Pm随着风速的增加而增加。以图9为例，在截止状态对应的P2拐点处L2 = 56.2 km，明显低于额定状态（L1），这进一步表明，对于高风速条件下，SL更为重要。

通过比较图8和图9的曲线表明，北方寒冷地区的Pm高于南方温暖地区。以漠河为例，与额定和临界状态相对应的转折点L值分别为L1 = 44.2 km和L2 = 54.5，均小于海口。结果表明，在寒冷地区，PSL和TSL的计算更为必要。

漠河和海口的Pm计算结果差异突出了不同的气候和地理特征，特别是环境温度和风速对WPI阈值的影响。如图所示，在一定条件下，SL代替TL成为关键限值，传统的基于TL的WPI阈值分析容易产生误判，尤其是在寒冷地区和长距离输电线路情况下。此外，虽然风力发电输出在额定和断电条件下运行时保持不变，但由于WPI阈值的变化，配电网能够接收到的有效功率可能会有所不同。考虑到同一环境条件下大型风电场与其输电线路之间风速的相关性，使得WPI的阈值估计更加实用可靠。

5   结   論

提出了一种计算WPI阈值的方法，该阈值由主系统最终能够接收的最大风力来定义。该方法可以根据环境和传输距离来识别不同极限（临界极限或热极限）的特征，从而通过考虑相应OTL的电热行为来获得更准确的WPI阈值。此外，假设风电场及其输电线路由于其相邻位置而假定风速水平相同，这种对风速相关性的处理使得当高风速同时影响发电和输电时的WPI性能。在不同的环境和传输距离条件下，关键限制因子和WPI阈值存在显著差异。最后利用两个环境因素独立的典型地点为例，验证了该方法的有效性。计算结果表明，在不同的环境条件下，该方法能够为综合风力发电提供精确可靠的数值，并清楚地说明了其局限性的原因。

参考文献

[1]    王园. 永磁电机在风力发电系统中的应用及其发展趋势[J].中国设备工程，2018（23）：201-202.

[2]    陈龙庆，周琛琛，梁华贵，等. 架空输电线路运行状态综合评价研究[J]. 吉林电力，2018，46（06）：9-12.

[3]    翟恩地，张新刚，李荣富. 海上风电机组塔架基础一体化设计[J]. 南方能源建设，2018，5（02）：1-7.

[4]    张丹. 风电管控一体化系统开发[J].电子技术与软件工程，2018（12）：46-47.

[5]    GONZ?LEZ-G?MEZ P A，G?MEZ-HERN?NDEZ J，FERRUZZA D，et al. Dynamic performance and stress analysis of the steam generator of parabolic trough solar power plants[J]. Applied Thermal Engineering，2019，147：804-818.

[6]    WANG M，YANG M，WANG J，et al. Contingency analysis considering the transient thermal behavior of overhead transmission lines[J]. IEEE Transactions on Power Systems，2018，33（5）：4982-4993.

[7]    ZIKRIA Y B，AFZAL M K，ISHMANOV F，et al. A survey on routing protocols supported by the Contiki Internet of things operating system[J]. Future Generation Computer Systems，2018，82：200-219.

[8]    BAIK H，VALENZUELA J. Unmanned aircraft system path planning for visually inspecting electric transmission towers[J]. Journal of Intelligent & Robotic Systems，2019，95（3-4）：1097-1111.

[9]    石军，潘晓春. 架空输电线路工程设计低温取值研究[J]. 电力勘测设计，2019（07）：77-80.

[10]  KALOR A E，GUILLAUME R，NIELSEN J J，et al. Network slicing in industry 4.0 applications：Abstraction methods and end-to-end analysis[J]. IEEE Transactions on Industrial Informatics，2018，14（12）：5419-5427.

[11]  MART?NEZ-RODR?GUEZ G，FUENTES-SILVA A L，PIC?N-N??EZ M. Solar thermal networks operating with evacuated-tube collectors[J]. Energy，2018，146：26-33.

[12]  余生. 架空输电线路规划设计与施工管理[J]. 机电信息，2019（20）：16-17.

[13]  裴慧坤，江克宜，黄顺发，等. 架空输电线路在线监测技术的开发与应用分析[J]. 电子测试，2014（23）：103-105.

[14]  CHOI T J，JANG S P，KEDZIERSKI M A. Effect of surfactants on the stability and solar thermal absorption characteristics of water-based nanofluids with multi-walled carbon nanotubes[J]. International Journal of Heat and Mass Transfer，2018，122：483-490.

[15]  齐宏纲，孙武，李庆祥，等. 指数律参数选取对指数和廓线精度的影响[J]. 华南师范大学学报（自然科学版），2017，49（05）：72-78.