基于时间序列的中小板指数短期预测分析

付子情 廉志辉 张凯峰

【摘要】首先，本文利用2008年1月4日到2020年4月10日这12年期间中小板指数收盤价的周数据来进行时间序列分析，拟合了相应的ARMA模型;其次，通过分析自相关图和ADF检验对所拟合的模型进行分析对比，并对其进行AIC准则和SC准则的检验，找到了最优的ARMA模型ARMA（2，2）;最后，得出中小板指数股价的发展趋势呈上升状态。

【关键词】中小板指数  时间序列  ARMA模型  短期预测

一、引言

中小板指数（399005）即中小企业板指数，指从深交所中小企业板上市交易的A股中选取的，具有代表性的股票。中小板指数将成为中小板投资者重要的参考工具，能够反映市场的总体波动特征，是市场的风向标。

时间序列数据通常用于描述现象随时间发展变化的特征。时间序列分析是根据客观事物发展的连续规律性，运用过去的历史数据，通过统计分析，进一步推测该事物未来的发展趋势。

二、模型方法

（一）ARMA时间序列模型

自回归移动平均模型（ARMA模型） 是研究时间序列的重要方法，它是由自回归模型（AR模型）与移动平均模型（MA模型）混合而成。一个ARMA（p，q）模型可以表示为：

（二）模型构建与预测流程

根据以往的研究，服从ARMA（ p，q） 模型的时间序列具有明显的统计特征，其自相关函数与偏自相关函数呈现拖尾或截尾现象，所以其模型的识别可以通过其自相关或者偏自相关的拖尾现象或者截尾现象来确定。

模型检验利用最小二乘法估计模型未知参数，并检验参数的显著性。通过对模型残差序列是否为白噪声检验模型本身的合理性。最后利用最优模型对数据进行预测并对结果进行分析评价。

三、实证过程与结果

（一）原始数据的平稳化处理

由于股市的波动较大，并且从图3.1中的中小板收盘价y的走势图中也可以看出收盘价y不仅有趋势项并且会随时间的变化有较大幅度的变化，通过Eviews软件分析原序列的自相关图得到t统计量对应的p值为0.07，大于显著性水平0.05，说明序列是非平稳的。

为了消除这种变化趋势使数据变的平稳，这里用差分法对原序列y进行处理，得到的一阶差分后的序列走势图，并对其进行了ADF检验。

进行差分后的序列已经没有趋势项并且在0上下波动，整体看来比较平稳。从图3.3的ADF检验结果可看出p值为0，小于显著性水平0.05，说明拒绝原假设，一阶差分后的序列不存在单位根，说明一阶差分序列是平稳的。

（二）ARMA模型的识别和选取

在得到平稳序列以后，需要对一阶差分序列的自相关图进行分析，找出ARIMA模型的滞后项p、q，然后根据滞后项的不同建立不同的ARMA模型进行分析检验，选取一个最优的模型进行预测。

d（y）的自相关函数和偏自相关函数均在滞后二阶的时候呈现截尾的现象，故这里选p=2，q=2。

为了确定我们得出的结果，这里用AIC准则和SC准则对模型进行检验。

从表1总结得出，ARMA（2，2）模型在AIC准则和SC准则下对应的值是最小的，并且ARMA（2，2）的模型中AR和MA的单位根的逆都在单位圆内，说明该模型拟合效果最好。最终得到的最优方程为：

△yt=1.472655yt-1-0.901142yt-2+εt-1.380516εt-1 +

0.819982εt-2  （3.1）

R2=0.057311   AIC=13.75294  SC=13.78134

（三）利用ARMA模型进行短期预测

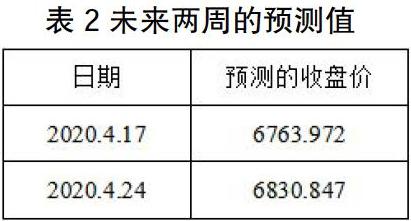
根据上面对ARMA模型进行的参数估计和检验结果得到的ARMA（2，2）模型来对中小板指数未来的收盘价进行短期预测，最后得到的预测值如表2。

故我们预测的4月17日的中小板指数收盘价为6763.972元，与4月1日的收盘价6705.05元相差不是很大，也说明我们预测的该指数在未来两周内可能呈现上升趋势。

四、结论

综上所述， ARMA模型可以较好的解决非平稳时间序列的模型构建问题， 在经济学研究的短期预测方面， ARMA模型具备一定的实用价值， 在一定程度上能够给投资者和决策者提供有用的信息和理论依据。但在股票市场上， 股价变动的影响因素有很多， 如宏观经济条件的变化、国际形势的变动以及公司内部结构的变化等等， 都会对股价的变动造成一定程度的影响。因此， 在股价的变动预测研究中， 后续我们仍需要不断的探讨和研究更加精确的模型。

参考文献：

[1]王苏生，王俊博，李光路.基于ARMA模型的沪深300股指期货高频数据收益率研究与预测[J].华北电力大学学报（社会科学版），2018，（03）：71-79.

[2]冯盼，曹显兵.基于ARMA模型的股价分析与预测的实证研究[J].数学的实践与认识，2011，41（22）：84-90.

[3]王丽娜，肖冬荣.基于ARMA模型的经济非平稳时间序列的预测分析[J].武汉理工大学学报（交通科学与工程版），2004，（01）：133-136.