时标上Leakage项变时滞BAM神经网络系统的概周期解*

高瑾，林园，王其如

（1. 深圳信息职业技术学院计算机学院，广东深圳518172；2. 深圳信息职业技术学院公共课教学部，广东深圳518172；3. 中山大学数学学院，广东广州510275）

Kosko［1−3］首先研究了一种新的神经网络系统，叫做双向联想记忆(BAM)神经网络系统。从此，BAM 神经网络系统被广泛地研究，它可以应用到图像处理，模式识别，优化问题，联想记忆等方面。在其应用中，神经网络系统的概周期解、周期解、渐近概周期解和伪概周期解等都是很具有吸引力的研究方向。因此，双向联想记忆(BAM)神经网络系统的概周期解被很多学者深入研究［4−8］。

经过多年的研究和发展，时标理论已经成为研究连续系统和离散系统的有效手段，具有广泛的应用前景，尤其在解的存在性、振动性、周期解、稳定性等方面发展迅速［9−10］。但是时标上BAM 神经网络系统的概周期解却很少被研究。

鉴于此研究的重要性，在本文中，我们将要研究以下形式的时标上Leakage 项变时滞双向联想记忆(BAM)神经网络系统：

其中i= 1，2，…，n，j= 1，2，…，m，t∈T，T 是一个概周期时标，n和m是每个细胞层的细胞数量，xi(t)和yj(t)分别是第i个细胞和第j个细胞时刻t的活动状态；ai(t)和bj(t)分别代表第i个细胞和第j个细胞和网络与外部输入在第t时刻脱节时，他们将电势重置为孤立情形下的休克状态的重置率；fi，fj是激活函数；αi(t)，βj(t)是时刻t的传递时滞；Kji，Lij是时滞核函数；Ii(t)和Jj(t)分别表示第i个细胞和第j个细胞时刻t的偏差。

系统(1)的初始条件为

其中φi，ψj∈C1(( −∞，0]T，R)且有界，( −∞，0]T ={t|t∈( −∞，0]⋂T}，i= 1，2，…，n，j= 1，2，…，m。

1 预备知识

本节我们给出一些基本的定义和定理［11−15］。

定义1［13］称T 是一个时标，若T 是实数集R 的任意非空闭子集并且继承实数集R 的拓扑结构和有序性。对于t∈T，时标上的前跳算子σ：T →T 定义为：σ(t)：= inf{s∈T：s＞t}；后跳算子ρ：T →T 定义为：ρ(t)：= sup{s∈T：s＜t}。

定义2［13］设T 是一个时标，t∈T 被称为左稠密点，如果t＞inf T 且ρ(t)=t；左稀疏点如果ρ(t)＜t；右稠密点如果t＜sup T 且σ(t)=t；右稀疏点如果σ(t)＞t。如果T 有一个最大的左稀疏点m，则Tk：= T{m}；否则Tk≔T。如果T有一个最小的右稀疏点m，则Tk：= T{m}；否则Tk：= T。

定义3［13］函数f：T →R 被称为左稠连续或者ld−连续函数，如果其在T 中的左稠密点连续，且在T中右稠密点的右极限存在。函数f：T →R 被称为右稠连续或者rd−连续，如果其在T 中的右稠密点连续，且在T中左稠密点的左极限存在。

定义4［15］设T 是一个时标，f：T →R，称函数f在t∈Tk是∇−可导，对任意ε＞0，若存在t的δ−邻域U(即U=(t−δ，t+δ)∩T)使得

定义7［14］时标T被称为一个概周期时标，如果∏：={τ∈R：t±τ∈T，∀t∈T}≠{0}。

2 概周期解的存在唯一性

本节，我们给出了系统(1)概周期解的存在唯一性的充分条件。

对于i= 1，2，…，n，j= 1，2，…，m，我们有如下表示：因此，由条件(H3)知，T是一个压缩映射。所以T在E中有一个不动点。也就是说，系统(1)在E中有唯一的概周期解。证毕。

3 概周期解的指数稳定性

本节，我们给出了系统(1)概周期解全局指数稳定性的充分条件。

4 例子和数值模拟

在本节，对于T = Z，我们给出一个例子来证明前面得到结果的正确性。

考虑下列BAM神经网络系统，n= 2，m= 2，

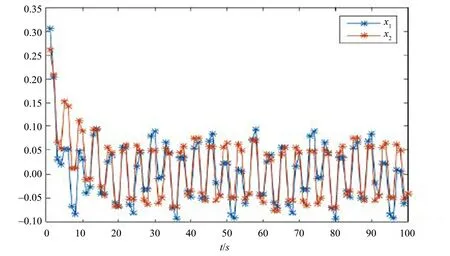
图1 状态变量x1和x2的轨迹图Fig.1 Transient response of state variables x1and x2

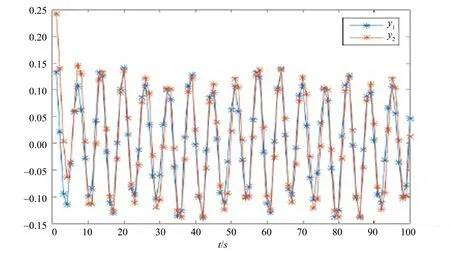
图2 状态变量y1和y2的轨迹图Fig.2 Transient response of state variables y1 and y2

5 结 论

本文给出了时标上的Leakage 项变时滞双向联想记忆(BAM)神经网络系统概周期解存在性、唯一性和全局指数稳定性的充分条件，另外还在T = Z 上，给出了一个例子和数值模拟来说明得到结果的正确性。本文所用的方法后续可以推广运用到其他神经网络系统的研究上。