基于马尔科夫模型分析DCS 系统可靠性

刘子琪， 袁 霞， 白 丹

（中国兵器装备集团自动化研究所， 四川 绵阳 621000）

0 引言

在安全等级SIL3 的核电工程中， 安全性检测DCS平台系统担当着安全核心作用。在以往，为了达到国际上SIL3 高安全性级别，所采用的安全检测DCS 系统均是采自于国外公司。运用可靠性框图、FTA 故障树从可能发生故障的方面来分析系统故障，对其可靠性进行分析。但这种方法去掉了随时间转变状态的系统情况， 如果考虑核电系统各种状态之间相互转换对其可靠性的影响则运用马尔科夫模型更为恰当。

马尔科夫模型是一种随机过程，并且在每个时刻中所可能发生的情况遵循着一定的概率统计规律。在系统增加了可修复的情况下， 马尔科夫模型能更好地描述投入使用后随时间变化时，刻画系统在某一时刻处于某种状态的概率，从而分析系统可靠性。 马尔科夫过程作为可靠性工程中的动态理论工具，现已广泛应用于许多的领域[1]。

本文利用马尔科夫模型对核电站安全性检测平台系统进行可靠性预测。 将该DCS 控制系统在使用过程中可能出现的各种正常及故障状态与马尔科夫过程相结合，建立了该系统的可靠性评估模型， 分析了该系统的各个状态概率。 为达到安全性级别要求和高可靠性提供了理论支持。

1 DCS 概念

核电厂DCS 数字化仪控系统。 核电厂DCS 系统可分为安全级（级） 非安全级（级） 。 在针对DCS 系统中的部分设计中，我们也采用了冗余设计的思路来符合核电控制仪安全性级别要求[2]。 1oo2D 结构冗余设计的思路，运用于所设计的输入模块、控制器模块和输出模块。 每个控制模块都设计有通道A、通道B 该两个通道，并最终由表决/切换电路决定输出。

2 马尔科夫过程

2.1 概念

马尔科夫过程在可靠性领域中是一种动态的随机过程。 如果其一步转移概率pij 恒于时刻t 无关，则称为齐次（时齐）马尔科夫。

本文研究的平稳马尔科夫模型是一种无记忆性的随机模型[3]。 在分析系统可靠性时，假设发生事件的时间服从指数分布，反映在马尔科夫转移率就为常数，即研究的模型是齐次马尔科夫模型。转移率λij是指在单位时间△t，从状态i→j 转移的期望值，当转移率为常数时，有以下关系存在：

式中，pi（t+dt） 为系统在某状态的概率；X（t）为系统在时刻t 的状态；X （t+Δt） 为系统在时刻t+Δt 的状态；ο（Δt）为在Δt 期间发生两次以上转移的概率。 当Δt 足够小时可得：

式中：n—总的状态数；I—单位矩阵。

在大多数情况下， 我们要得到的是系统长期工作时的平稳状态概率pi ，可求解线性代数方程组

式中，P—各平稳状态概率pi 组成的矩阵。 由此得马尔科夫过程的研究对象是可修复系统。 到系统在各个可能状态的状态概率， 并可进一步求出其它的系统可靠性指标。

2.2 核电安全性检测平台系统的可靠性特征

首先该系统是一个可修复系统。当系统发生故障后，一首先诊断故障部位，对其进行修理或更换，直到恢复到正常工作状态，该工作过程即为修复过程。电子器件的老化过程是一个呈“浴盆曲线”，一般是从正常工作状态转移到故障状态，然后经过修复回到正常状态，如此往复循环下去。 失效状态转移到另一种状态的“状态转移”完全是随机的。 但是在诊断出失效后，进行故障修复。 这种修复状态转移是可以刻画为常数矩阵的。 用马尔科夫过程求DCS 平台的可靠性指标时，主要讨论的是核电安全性检测平台投入使用后达到平衡状态时的工作情况， 即故障率和修复率都为常数， 各部件的寿命和维修时间均服从指数分布，让这些条件满足马尔科夫过程的基本假设。

3 核电安全性检测平台马尔科夫模型的建立

3.1 划分故障状态

由于DCS 及其外部电路都是由半导体集成电路（IC）、晶体管和电阻电容等器件构成，这些电子器件不可避免的存在失效率的问题。 所以这些器件的可靠性将直接影响DCS 系统的可靠性用状态，将系统的非运行状态进行分类，作为独立的状态变量予以考虑。 系统运行后，就作为统计对象进入使用状态， 使用状态分为可用状态和不可用状态，其状态分类如图1 所示。

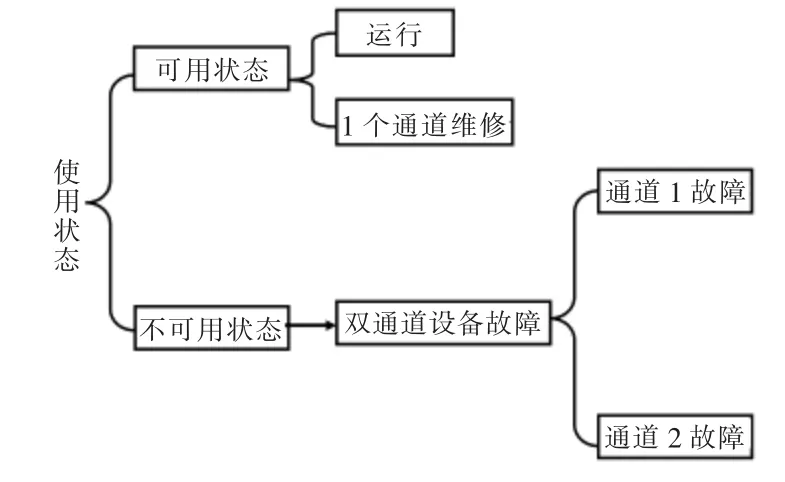
图1 带双通道使用状态分类

图2 1oo2D 结构冗余设计

为提高DCS 的可靠性， 具体设计的I/O 模块， 控制器，电源，网络以及服务器，都进行1oo2D 冗余设计。

该结构未专门设置备用通道 （不采取3oo2D 结构），只要不处于故障维修或预防检修的状态， 所有板卡均全部投入使用。

3.2 马尔科夫模型的建立

假设在上述图2 的模型中输入模块、主控制模块、输出模块进行每运行一段时间τ，诊断电路对系统进行一次诊断。多通道马尔科夫原理见下图3。工作（W）、未被检测到的危险失效（DU）、正在进行修复（R）。

图3 带诊断电路的DCS 系统马尔科夫模型

图3 所描述的马尔科夫过程为在诊断间隔的系统工作时间段τ 中： 多冗余通道的系统某一通道部位可能从工作状态变为危险失效（W→DU）也可能处于修复到工作状态（R→W）。 在这期间因为没有发生诊断工作，所以不可能出现DU→R。

μ 代表组件部位的修复率（μ=1/MRT），λ 表示失效率。

在单通道诊断系统时刻， 发现危险失效并开始修复（状态转换为DU→R），工作运行正常（W→W），正在修复（R→R）[4]。 因此，带诊断电路的状态转移矩阵如下：

图4 中字母A 和B 代表双通道，粗字体代表通道处于工作状态，细字体代表通道处于失效状态。 λa、λb表示A、B 通道的失效率，λccf表示系统的失效率；μa、μb表示修复率。

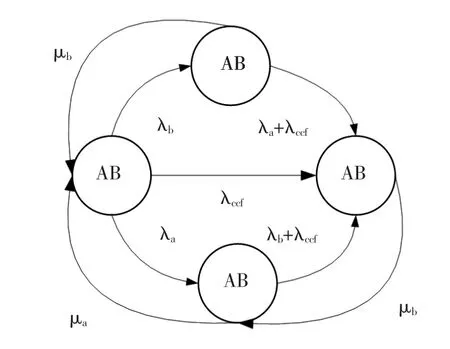
图4 双通道带诊断的系统状态图

根据图4 的双通道带诊断该1oo2D 结构系统状态图，以及上述公式，可推出转移矩阵[M]：

式中：θ—在每次诊断间隔期间的任意时间。

根据西门子电子器件失效率数据手册计算各个板卡模块（例如通信模块、AI 模块、表决模块等）的失效率，再加总得通道A 的失效率。 假设通道A、B 选择的电子器件一致，则λa=λb=1.56×10-5。 μ=1/MTTF。 求得转移矩阵[M]，再带入式（9）。可以得到如图5 的阶段性锯齿状失效率图。可知在每次诊断修复后，失效率大幅降低，在随后使用过程中失效率升高。 又到下次诊断修复后， 失效率大幅下降。 继而形成一种随诊断时间间隔而来回波动的状态。

4 基于马尔科夫核电检测平台冗余模块可靠性

图5 中虚线用PFDavg（T）表示整个过程中系统平均失效率。

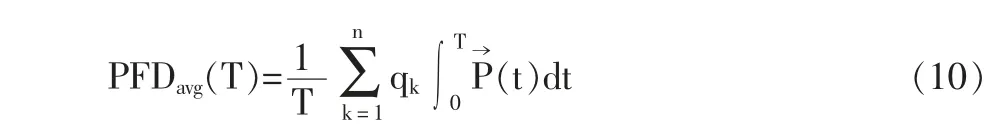
带有下标k 表示在时间段T 期间的状态k 的失效率，qk表示状态k 的权重。 qk在此一般为0 或者为1。

5 结束语

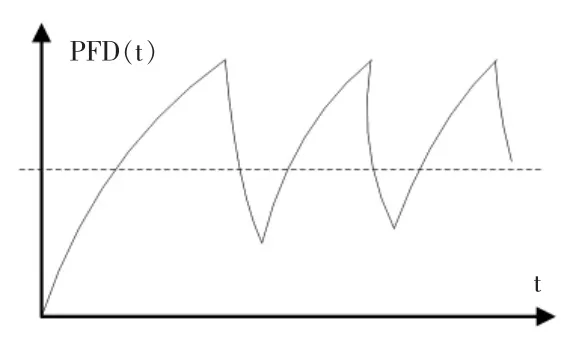
图5 锯齿状多通道马尔科夫过程图

本文将DCS 系统双通道A、B 运行后可能所处的状态划分为系统正常运行、通道A失效状态、 通道B 失效状态，以及整个系统失效。 在这种状态转移分析下，给出转移矩阵[M]。 不仅如此，在每间隔时间τ 进行诊断的基础上提出了带系统修复的情况，给出了修复矩阵[L]。 在系统运行时，既发生状态转移[M]又在间隔时间诊断后发生修复状态转移[L]。

因此该模型能很好地反映出DCS 系统在各个时间处于各个状态的概率， 给出了带诊断且发生修复的实际过程中的可靠性指标。

从拟合数据图5 看出， 该模型能通过计算随时间t状态变换矩阵以及在间隔时间诊断后进行修复时的状态变换矩阵， 通过双重分析能较准确地对DCS 平台1oo2D可靠性进行量化评估。 反映出一段时间内系统失效率增高，在诊断后进行修复有效地降低了失效率。在随后系统失效率又开始增高，又通过诊断修复降低失效率。周而复始，形成锯齿状的系统失效走势。本文所探讨的马尔科夫过程还可以应用于其它带诊断修复领域的失效率预测中，对1oo2D 结构平台实际运行过程进行可靠性的预测。