永磁无刷直流轮毂电机建模及模态分析

葛 畅， 崔朋涛， 陈佳浩， 苏丹丹

（1.河北大学 质量技术监督学院， 河北 保定 071000； 2.保定长安客车制造有限公司， 河北 定州 073000）

0 引言

汽车工业的快速兴起无疑使得人类的生活、 工作更加方便快捷，但随着汽车总量的快速增加，尾气排放加重了环境污染，石油资源消耗过快。现如今汽车工业技术转移的重要目标就是缓解上述问题， 纯电动车无疑是各大汽车厂商最理想的选择。 早在1993 年，美联邦政府和各大汽车公司为全面研究各类新能源概念车投入了大量的资金和技术，之后欧盟也推出FP 计划，日本由于石油匮乏，对电动汽车的研发时间更早[1]，十一五期间，中国制定新能源汽车的发展规划，国内各大汽车厂商积极研发。

传统内燃机汽车复杂的传动系统使得传动效率、能源利用率降低[2]，电动汽车在传统汽车的基础上演变创新，按照驱动形式的不同分为集中电机驱动、 轮边电机驱动及轮毂电机驱动。

轮毂电机将动力源、动力输送装置、制动装置安装在轮毂内，大大简化了车辆结构，在行驶过程中的车内噪声极低，提高了传动效率以及能源利用率，被看作未来纯电动汽车最佳的驱动形式[3]。 但因其使得簧下质量增大，导致减震效果差，使汽车整体舒适性降低，这就对轮毂电机的设计提出了更高的要求。

本文选用某型号永磁无刷直流轮毂电机， 对其进行建模和模态分析，得出其前六阶的固有频率以及主振型。

1 轮毂电机实体模型建立

1.1 轮毂电机的实体模型建立

利用NX 8.0 进行实体建模，通过拉伸、旋转等建模方法，并且运用布尔运算加以辅助，使用户既可以参数化建模，又可以使用非参数化方法建立三维模型，方便对复杂的机械零件进行模型建立。 并且在完成建模后，能够进行测量和简单物理特性分析。

建立各结构模型时对其进行适当的等效与化简，忽略倒角、圆角以及螺栓处的螺纹，将永磁体形状和硅钢片整体等效成圆柱形，模型如图1 所示。

图1 轮毂电机外形图与爆炸图

1.2 三维模型误差分析

在轮毂电机的测量过程中， 总会存在测量误差，这些测量误差必然导致建立的三维模型与实际零件有所偏差， 建立模型过程中的等效简化也会导致偏差有所增大。 基于以上情况，需对其偏差进行误差验证， 通过电子秤测得各结构实际重量，并且在NX 8.0 中对实体模型赋予其材料密度，对比相应数据得出模型误差。

根据轮毂电机厂家资料， 可得出其关键部分结构的材料物理特性，如表1 所示。

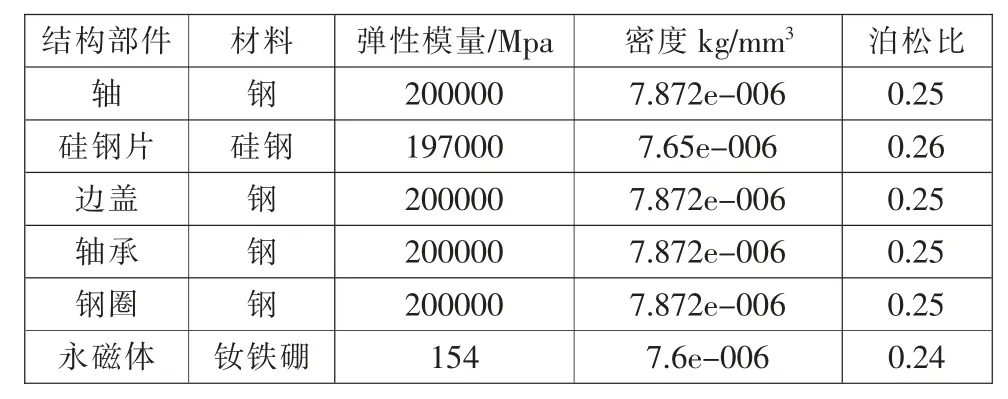
表1 各结构材料物理特性

分别对轮毂电机各结构赋予其相应材料实体密度，得到所建模型的重量，并且与电子秤所得重量进行比较，计算误差，结果如表2 所示。

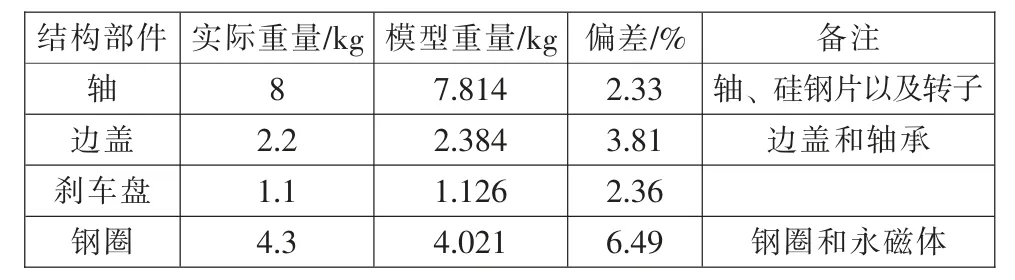
表2 各结构重量误差

结果可以看出除电机钢圈外， 其余结构重量偏差均在5%以下，三维模型与实际结构偏差较小，对有限元模态分析仿真的影响能够控制在较低的范围内； 电机钢圈误差为6.49%，低于10%，与其他结构相比误差较大，但总体误差对有限元模态分析结果的影响有限。

2 模态分析理论

模态是机械结构固有的振动特性， 其只与结构自身性质有关，有确定的固有频率和振型。分析计算模态参数的过程就是模态分析。

轮毂电机各结构都是有质量的， 一般系统可以描述为具有多个自由度的系统。 在对各结构进行有限元分析时，需要先建立有限元模型，然后对其离散处理，这样就成为了一个n 自由度的有限个单元组成系统， 各结构的振动微分方程为：

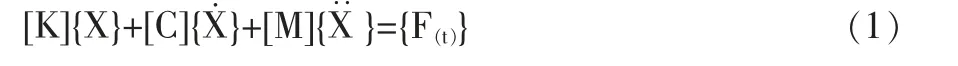
式中：[M]—质量矩阵；[C]—刚度矩阵；[K]—阻尼矩阵；{X}—位移向量；{F（t）}—外部激励力向量；{X˙}—速度向量；{X··}表示加速度向量。

模态分析解决了系统的固有特性， 即固有频率及振型，因此可忽略外部载荷的影响，故{F（t）}为零；在工程应用中，忽略阻尼对模态分析的影响，故[C]为零，根据式（1）可化简成无阻尼振动运动方程：

结构在自由状态下时做简谐运动， 即位移向量为正弦函数，有方程：

式中：X0—各节点振幅向量；ω—振动频率；t—时间。

将式（3）代入式（2）可得：

在自由振动的状态下，X0不全为0，所以式（4）特征方程有：

可知n 自由度系统的刚度矩阵和质量矩阵都是n 阶的，所以方程特征值为ω2，其开方后就是n 个固有频率。固有频率为f=ωi/2π，特征值ωi对应的特征向量{X}i为固有频率f=ωi/2π 对应的振型。

3 电机各结构有限元模态分析

本文使用NX 8.0 软件对轮毂电机进行实体建模和有限元分析。结构分析模块中选用为NX Nastran 求解器，解算方案中选用SEMODES 103 动力学分析，应用以上求解器以及求解方案，只需添加材料物理参数、网格密度和边界条件便可实现有限元模态分析。

3.1 轮毂电机模态求解

结构本身的材料物理性质是影响模态分析的重要因素，其中主要包括密度、弹性模量以及泊松比，这就需要了解电机各结构的材料物理参数，具体参数如表1 所示。

3.2 单元选取和网格划分

NX 8.0 中的结构分析模块有四节点和十节点四面体，本文选择十节点3D 四面体网格，可根据实际情况决定单元大小，以电机边盖为例，本文将电机边盖的自动单元大小除2，单元尺寸为4.29，最终整个电机边盖划分网格单元数36207 个，网格节点数72722 个，生成的网格如图2 所示。

图2 电机边盖的Fem 模型

3.3 边界条件及求解

图3 添加边界条件后的Fem模型

以电机边盖为例， 本次求解的是自由状态下的模态分析， 即无外界激励， 因此不添加载荷以及约束条件；在拆解过程中可知， 由于端盖以及轴承的过盈配合使得拆解十分困难，将端盖以及轴承看为一体， 因此在仿真过程中需将轴承和端盖添加 “面对面粘合”指令，最终求解得出结果。

3.4 结果分析

对各结构固有频率以及主振型进行整理。

由图4 可以看出各结构固有频率随阶数的增大而增大，不同结构的增长幅度也不尽相同，模态振型也随着阶数增长而变得越来越复杂，反映出了系统本身结构的固有特性。 结构是否发生共振主要取决于低阶固有频率，从结果中可以看出，所有结构的一阶固有频率均在200Hz 以上，高于实际工况的振动频率，故不会发生共振，也不会影响车内乘坐舒适性。

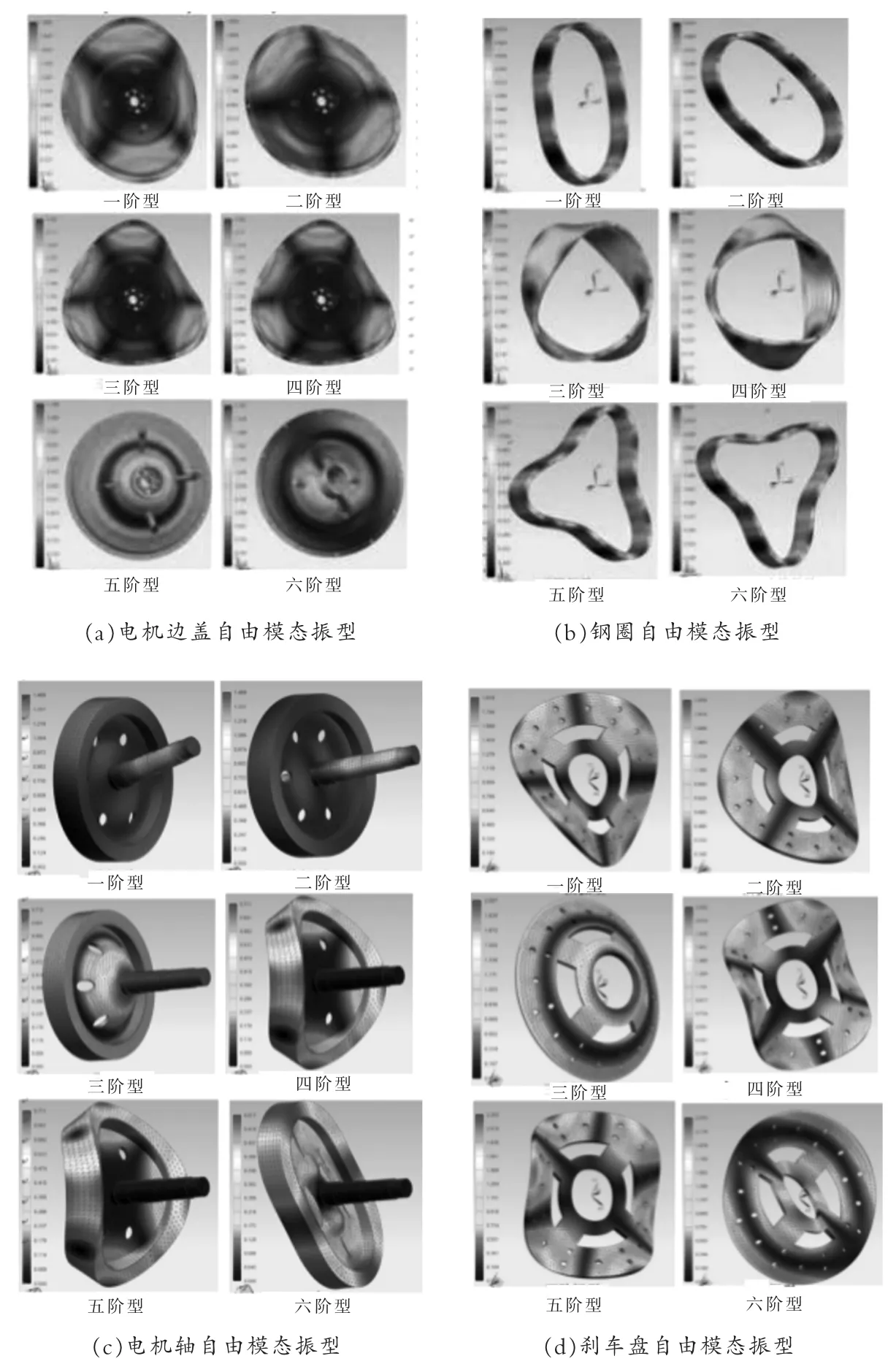
图4 电机各结构自由模态振型

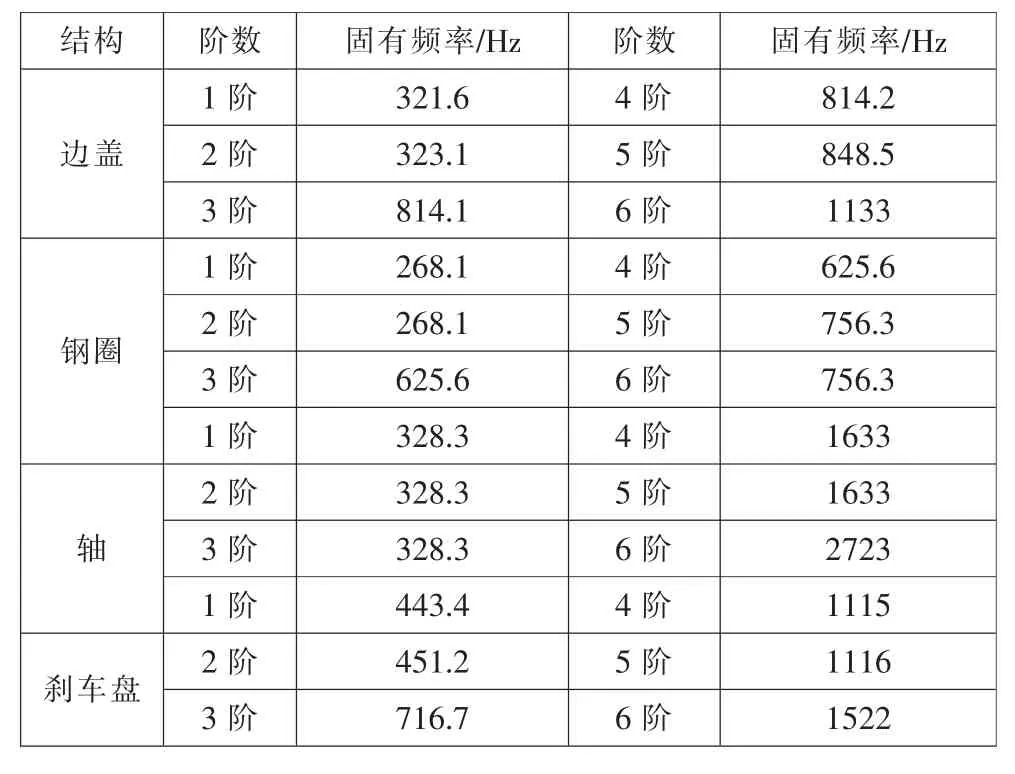
表3 各结构固有频率

4 结束语

本文采用软件NX 8.0 建立了某型号永磁无刷直流轮毂电机的实体模型， 并采用NX Nastran 进行有限元法模态分析， 计算出自由状态下电机各结构前六阶的固有频率以及主振型，认识到了各结构本身的固有属性，为今后该型号轮毂电机的设计优化提供了初步的数值依据。