用温度计测量酒精的体膨胀系数

罗 倩，张皓晶

(云南师范大学 物理与电子信息学院，云南 昆明 650500)

热膨胀系数决定了给定物质随温度增加或减少扩张的能力,可以分为线性膨胀系数、面积膨胀系数和体积膨胀系数. 传统上，液体的体积膨胀系数由膨胀仪测量，例如，实验中可直接由膨胀计得到水的体积膨胀系数[1]. 由于酒精的热敏性，在讨论热膨胀现象时，酒精已成为传统教科书和章末习题中涉及最多的物质之一. 本文旨在用简单的方法和实验装置获得酒精的体积膨胀系数.

1 实验原理

1.1 已知球茎截面和球泡体积的温度计

温度计毛细管1中的酒精体积随温度的变化而膨胀或者收缩，温度改变量ΔT1与体积的变化量ΔV1之间成正比例关系[2]，即

ΔV1=γ1V1ΔT1,

(1)

式中，γ1和V1分别为酒精的体积膨胀系数和初始体积(在一定的初始温度下，玻璃温度计球泡和毛细管中酒精的总体积). 式(1)可以写为

(2)

式中，A1为温度计毛细管的横截面积. 式(2)中ΔL1与ΔT1线性相关，设其斜率为S1，即

(3)

通过拟合ΔL1-ΔT1获得斜率S1，根据已知数据点长度的变化ΔL1和温度的变化ΔT1，代入最佳拟合直线的斜率S1,从而获得酒精的体积膨胀系数γ1.

1.2 球茎截面和体积未知的温度计

毛细管2的横截面积为A2，初始体积为V2(在一定的初始温度下，球泡和毛细管中酒精的总体积). 由1.1可知以下关系成立：

ΔV2=γ2V2ΔT2.

(4)

(5)

(6)

式中,ΔT2为温度改变量，ΔV2是酒精相应体积变化量，γ2和V2分别为酒精的体积膨胀系数和初始体积.

将γ1的表达式(3)和γ2的表达式(6)等效,得到：

(7)

由式(7)可得：

(8)

因为

(9)

(10)

对于任意初始体积(V1和V2)、截面面积(A1和A2)以及最小的温度间隔都不同的温度计，在实验中可以使温度的变化ΔT1和ΔT2相等. 因此，由式(9)和式(10)可得:

S1ΔL2=S2ΔL1,

(11)

代入式(8)时，得到：

(12)

将式(12)代入式(6)得到

(13)

由式(13)可知ΔL1和ΔL2线性相关，斜率S3为

(14)

在已知S3，S2，V1和A1情况下，可以通过式(14)得到酒精的体积膨胀系数.

2 实 验

2.1 已知球茎截面和球泡体积的温度计

实验装置如图1所示，ΔL为长度的变化,Lf是升温到最高温度后的长度. 酒精温度计1的量程为100 ℃，精度1 ℃，酒精柱的高度从温度计的下端到35 ℃的标高为L0=18.10 cm，A1=1.2×10-3cm2. 烧杯内装热水，并用卷尺测量一定温度下酒精柱的高度. 设球泡中酒精的体积为V1′，已知等于0.12 cm3. 固定初始温度为35 ℃，将温度计浸入盛热水的烧杯中，使温度稳定在35 ℃. 测出35 ℃相对于球泡顶端对应的酒精柱高度为16.5 cm，毛细管中酒精的体积为0.019 8 cm3，酒精的初始体积V1为0.139 8 cm3.

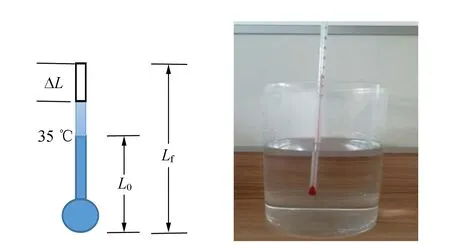
图1 实验装置

采集ΔT1和ΔL1的数据时，将温度计浸入盛热水烧杯中，改变热水的温度，从而将酒精的温度从35 ℃升高到稳定的最终温度Tf1. 在特定的最后温度下，用单独的温度计读数，测量相对应温度下的高度，再将得到的变化长度减去18.10cm，得到酒精在特定温度下伸长的长度ΔL1. 同样，Lf是相对于温度计球的下端测量的. 类似地，温度ΔT1也要减去初始温度35 ℃. 测量8个数据，每次酒精的初始温度都为35 ℃. 实验数据见表1.

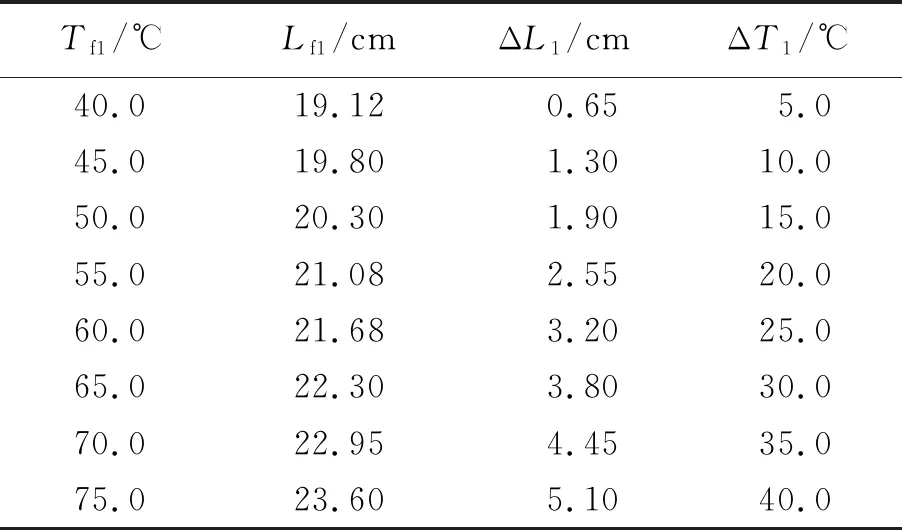
表1 实验数据1(T0=35.0 ℃，L0=18.10 cm)

ΔL1-ΔT1图像如图2所示，使用Excel拟合数据,得到长度变化与温度变化的线性关系. 解得体积膨胀系数γ1=1.08 8×10-3℃-1. 通过查阅文献[3]得酒精体积膨胀系数的值为1.1×10-3℃-1,相对偏差为1.1%.

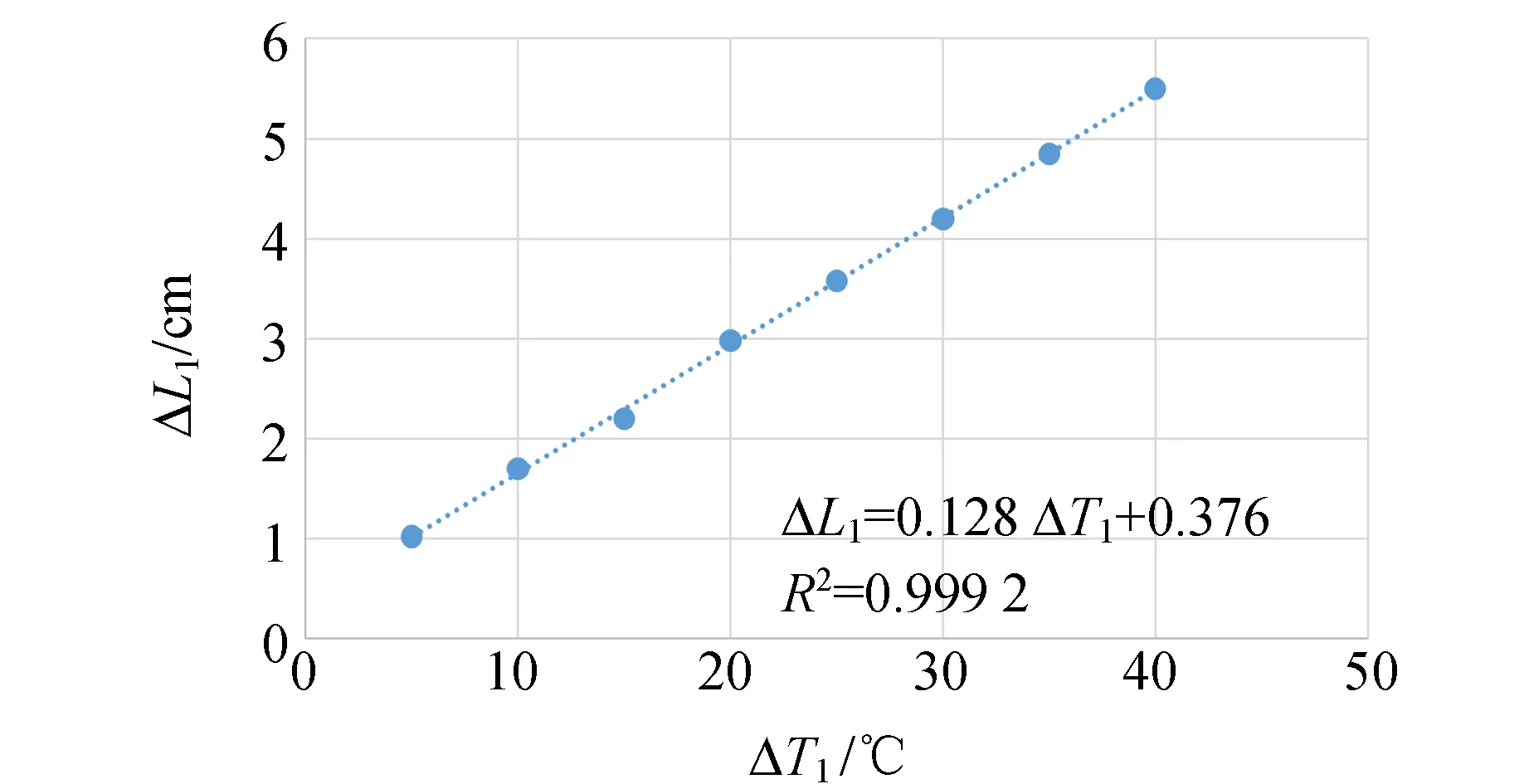
图2 ΔL1-ΔT1图像

2.2 球茎截面和体积未知的温度计

温度计2的量程为200 ℃，精度为2 ℃，酒精柱从温度计的下端到35 ℃的标高为13.70 cm，球泡的体积和茎的横截面积未知. 采集数据点ΔL2和ΔT2. 按照2.1步骤完成实验，但有约束条件，即所有的温度变化ΔT2应等于2.1实验得到的温度变化ΔT1[与式(10)一致]. 此外，将初始温度固定在35 ℃，同时将初始温度提高到与2.1相同的最终温度Tf2. 对应温度变化ΔT2，取对应的高度变化ΔL2，其值应与ΔL1不同. 实验数据见表2. ΔL2-ΔT2图像如图3所示，使用Excel拟合数据,得到长度变化与温度变化的线性关系,其斜率为S2=0.064.

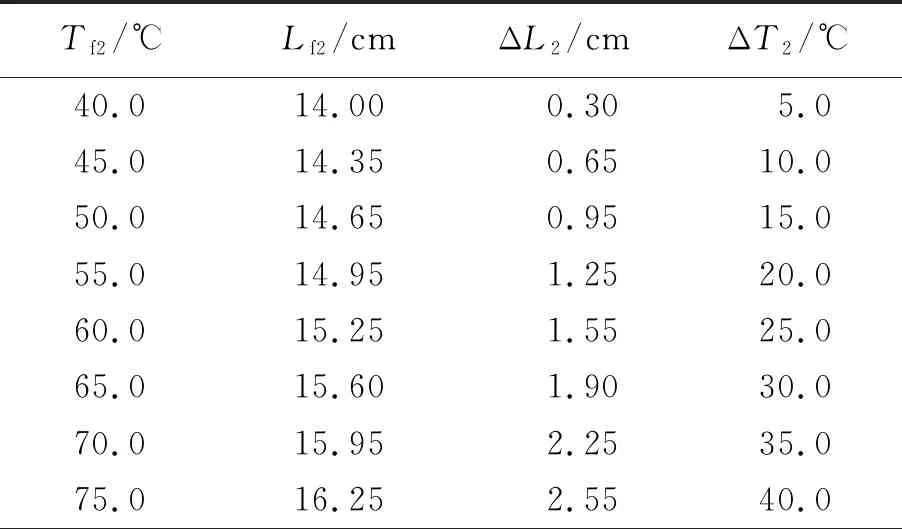
表2 实验数据2(T0=35.0 ℃，L0=13.7 cm)

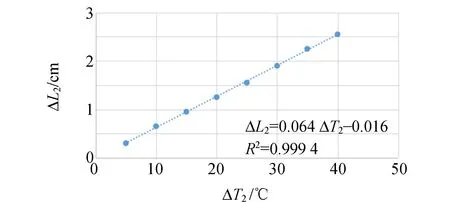
图3 ΔL2-ΔT2图像

绘制ΔL1-ΔL2,如图4所示,并进行线性回归得S3=1.978. 将S3代入式(14),由已知A1,V1和S2,得到酒精的体积膨胀系数γ=1.086×10-3℃-1，与标准值1.1×10-3℃-1[3]的相对偏差为1.3%.

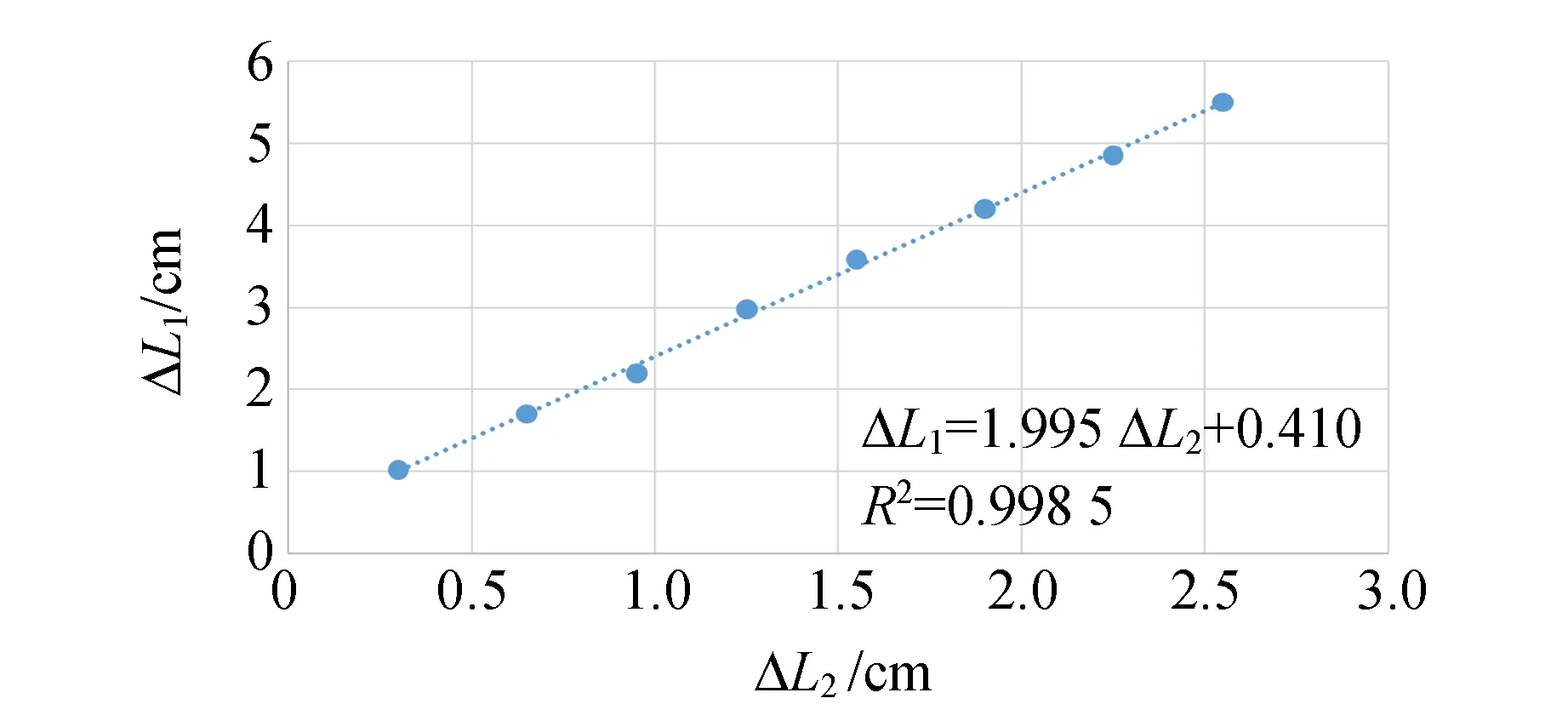
图4 ΔL1-ΔL2图像

4 结束语

利用生活中常见的材料，设计了简便易行的测量或演示酒精体积膨胀系数实验装置. 学生参与实验，体验学习物理的乐趣. 教师可选择2.1实验(V1和A1已知)，通过酒精柱长度变化提供多对数据点来计算酒精的体膨胀系数. 2.2实验(V1和A1未知)需要理论推导和一定时间的实验室活动，因此2.2实验可作为学生课外兴趣实验，加深学生对膨胀系数的理解及应用.