基于Markov过程的IaaS系统可用性建模与分析方法
杨哂哂,吴慧珍,庄黎丽,吕宏武
(1.上海商学院网络中心,上海 200235;2.哈尔滨工程大学计算机科学与技术学院,哈尔滨 150001)
(*通信作者电子邮箱lvhongwu@hrbeu.edu.cn)
0 引言
云计算(cloud computing)是一种典型的效应计算模式,允许用户像购买水电一样以“按需使用的方式”采购计算服务,极大降低了计算密集型服务的成本[1]。美国国家技术标准与技术研究院(National Institute of Standards and Technology,NIST)将云计算划分为三个层次,包括基础设施即服务(Infrastructure as a Service,IaaS)、平台即服务(Platform as a Service,PaaS)和软件即服务(Software as a Service,SaaS)。其中IaaS 大多出租给基础服务运营商(Infrastructure Service Provider,ISP),为终端用户提供可以随时部署操作系统和应用的基础计算环境;IaaS 的提供商一般和用户签署有服务等级协议(Service Level Agreements,SLA),主要规定了服务的可用性等级以及相应的违约惩罚;IaaS 对服务的可用性具有更高要求,任何不可用的状态都将对其商誉和收益带来极大损失[2]。因此,高可用性对于IaaS具有更重要意义。
目前已经有大量工作对IaaS 的可用性进行了研究,包括物理机器(Physical Machine,PM)排队机制、虚拟机器(Virtual Machine,VM)迁移和异构工作流影响等。文献[3-4]重点研究了VM 迁移对可用性的影响,但是PM 对于IaaS 云系统可用性的影响更加基础化。文献[5-6]研究了基于容器的IaaS 的可用性,但是考虑到容器的安全隔离性问题还没有得到全面解决,在可预见的将来并不能完全取代现有VM 方式。文献[7]中分析了批量任务等异构工作流对云计算系统可用性的影响,在此基础上文献[8-9]分别对不同的PM 分配策略进行了研究。与从任务流角度分析可用性不同,本文遵循文献[4]仅关注于IaaS 系统对于任务处理的思路,屏蔽任务流的复杂性,这也是本领域绝大多数研究采用的方式。此外,其他大量研究还分析了VM 容量规划[10]和关键影响因素分析[11]等问题。本领域的主要工作还集中在PM 队列调度策略对可用性的影响,在文献[12-15]中主要研究了不同PM 队列调度策略对可用性的影响,但目前的研究主要分析至少存在一个VM可用的概率,不能分析存在任意N个VM 可用的情况,无法满足批任务同时需要N个VM 时云计算系统服务可用性的分析。
据此,本文提出了一种IaaS系统可用性分析方法,通过建立IaaS 系统PM 分配的状态转移概率空间模型,描述PM 失效、恢复以及成功部署任务的概率,从而获得系统处于可用状态的稳态概率。本文研究可以用于定量分析一个IaaS系统存在任意多个可用PM的概率。
1 基于Markov过程的可用性模型
1.1 模型的建立
IaaS系统规模巨大,能够包含数以百万计的计算节点,据相关报道其能耗相当于一个美国中型城市。为了节能通常将IaaS 计算节点分为hot PM、warm PM 和cold PM 三类。hot PM可以直接部署VM 并运行服务,部署时延极短;warm PM 又称为hot standby PM,它处于热待机状态,在部署VM 之前有一定时延;cold PM 又称为cold standby PM,PM通常处于关机状态,需要较多时间部署VM。每一种PM 都会被组织成一个资源池,由系统进行调度。
为了简化可用性建模,假设IaaS 可用性仅与计算资源的可用性相关,所有其他原因引发的不可用状态都可以等价于计算资源的不可用。同时,由于IaaS 主要提供基础设施给云服务提供商,因此关注的重点在于PM 的分配,且VM 部署的影响在其他文献[2-3,7]中已有研究,本文不再作为重点。在此基础上,对系统可用状态的描述,将转化为对PM 分配过程的建模。假设每次任务到达时,请求分配一个正常且可部署VM的PM,当需要分配多个VM 时等价于多次任务请求。上述三种PM 所处的状态均可以分为三类:正常且可部署VM 的PM、失效PM 和正常已部署满VM 的PM,于是系统状态可以用当前时刻所有PM所处状态来刻画。
假设系统在时刻t的状态为St,为了表述简便当不指定特定时刻时简记为:

其中:ξhot=(Nhot,Dhot,Fhot);ξhot各元素分别代表正常且可部署VM的PM数量、正常已部署满VM的PM数量和失效PM数量。同理,ξwarm=(Nwarm,Dwarm,Fwarm),ξcold=(Ncold,Dcold,Fcold)。
本文借鉴现有IaaS 可用性模型[10,13],建立一种基于Markov 过程的IaaS 可用性模型,按照PM 资源分配的三个阶段分别对应三种PM 分配子模型。三种PM 分配子模型分别用于描述hot PM、warm PM 和cold PM 资源池内部的PM 调度,包含PM 的失效、VM 成功部署和释放。IaaS 会优先选择hot PM 分配子模型,从hot PM 资源池中分配PM;若不存在则依次由warm PM 和cold PM 分配子模型查找剩余的两个资源池,若仍然没有可用的cold PM,则进入不可用状态Unavail。当服务完成后,将PM 挂起,为了节省能源,优先填补到低能耗的资源池中,且保持各资源池中PM 数量不变。三种子模型通过计算资源的转换关系相协作,构成系统整体模型,原理如图1所示。
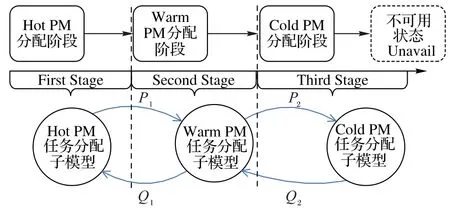
图1 可用性模型的原理Fig.1 Schematic diagram of availability model
其中每一个子模型都对应一个Markov 链,将在1.2 节中分别论述,由有限个Markov 链简单组合而成的系统模型也是一个Markov 过程。而各子模型之间状态转移概率P1、P2、Q1、Q2可以通过各子模型的转换关系求得。本文采用采用经典的Lv 方法[8]计算状态转移概率,假设每个转移动作的延迟都服从指数分布,转移概率为动作时延的数学期望的倒数。
1.2 PM分配子模型
1.2.1 hot PM分配子模型
hot PM 子模型如图2 所示。假设初始时刻ξhot=(h,0,0),状态之间的转移分为横向和斜向两个部分,其中,横向负责PM 资源的分配和释放,斜向描述了PM 失效过程。IaaS 系统先判断正要分配的hot PM 是否已经失效,如果没有失效,就正常分配PM,Dhot的数量就会增加。如果发现将分配的hot PM失效,那么进行斜向转移,Fhot的数量就会增加。由于ξwarm、ξcold在此过程中保持不变,系统初始状态S可以记为一个分块矩阵,

其中:H23=。
当最终不存在hot PM,将由整体模型控制转入warm PM分配子模型。每一个warm PM 分配子模型可以用系统此时包含的hot PM 的状态唯一标识,例如warm PM 分配子模型W(h-i,i)代表当有i个PM 已经失效,其余(h-i)个hot VM 已分配完毕时转入此子模型。
1.2.2 warm PM分配子模型
warm PM 分配子模型负责对warm PM 进行资源分配。不失一般性,以warm PM 分配子模型W(h-i,i)为例进行讨论。记此时的ξhot状态为H1=(0,h-i,i)。若warm PM 资源池中初始有w个PM,则起始状态可以表示为:

其中:H3=ξcold,而H1和H3在状态转移过程中保持不变。warm PM 分配子模型W(h-i,i)的资源分配对应的Markov 过程与hot PM 分配类似,如图3 所示。当最终不存在hot PM,将由整体模型控制转入cold PM 分配子模型。每一个cold PM 分配子模型可以用系统此时包含的hot PM 和warm PM 的状态唯一标识。
1.2.3 cold PM分配子模型
cold PM 分配过程与hot PM 和cold PM 类似,也可以描述为一个Markov 链。不失一般性以标号为的cold PM分配子模型为例进行讨论。在此子模型中,初始时刻ξhot=(0,h-i,i),ξwarm=(0,w-j,j),cold PM 资源池中初始有c个PM,则起始状态可以表示为:

其中:H12=。
因此,cold PM 分配过程如图4 所示,其中H12在此过程中保持不变。
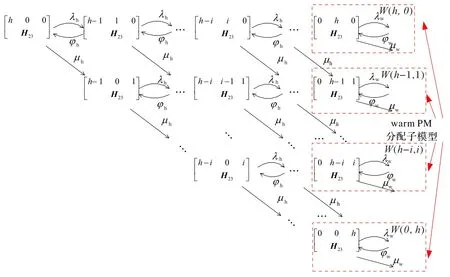
图2 hot PM分配子模型Fig.2 hot PM allocation sub-model
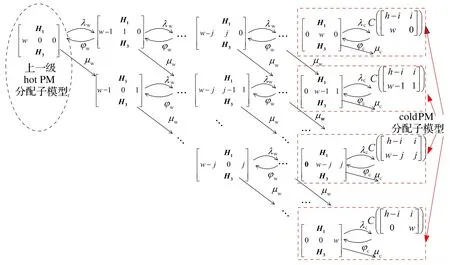
图3 warm PM分配子模型W(h-i,i)Fig.3 warm PM allocation sub-model W(h-i,i)
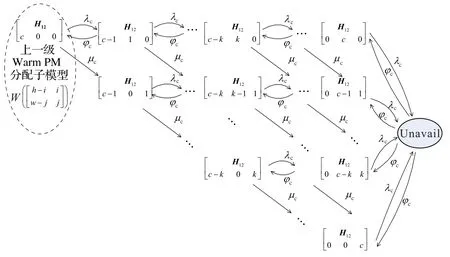
图4 cold PM分配子模型C(h-i,i;w-j,j)Fig.4 cold PM allocation sub-model C(h-i,i;w-j,j)
2 模型求解
本文采用稳态概率方法对模型进行求解,进而在此基础上对可用性进行评估,避免了设定指标权重系数的人为干扰。
首先,将系统所有状态表示为一个向量。
若初始状态hot PM、warm PM 和cold PM 的数量分别为h、c、w,由图2~4 可以得到共有1 个hot PM 子模型,(h+1)个warm PM 子模型和(h+1) ×(w+1)个cold PM 子模型,则整个模型除了状态Unavail共有状态数量:
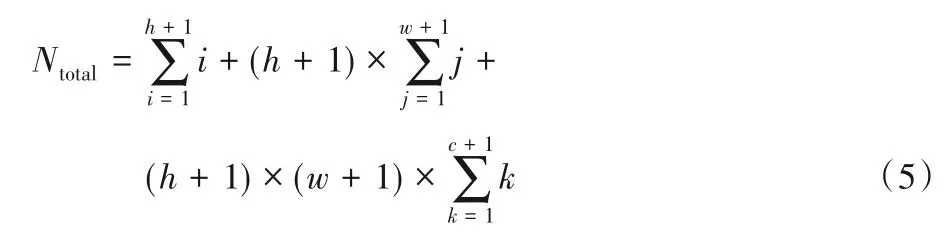
由式(1)可知,状态S的任意一个矩阵SS可表示为:

为了表示的方便,将这些状态按照矩阵S的所有元素Sij组成的向量(S11,S12,…,S33)的各元素数值依次由小到大排序,序号分别为1,2,…,Ntotal。
在排序之后,可以利用现有的Markov 过程求解稳态概率公式求解每一个状态的稳态概率[4,7]。若πS代表状态S的稳态概率,所有πS和πUnavail组成稳态概率向量Π=(π1,π2,…,πNtotal,πUnavail),Q为一步状态转移概率矩阵,且Q=(quv)。其中Quv表示从状态u到状态v的转移概率,u,v∈{1,2,…,Ntotal,Unavail}。则稳态概率[4,7]可以用式(7)求解。

3 仿真实验与结果分析
本章将通过实例验证IaaS 可用性评估的有效性,主要是由于系统实测的可用性分析方法存在诸多限制:1)需要长期观察云计算系统的运行状况并记录故障次数,涉及不同时间段、不同硬件主机和不同虚拟机的运行并进行大量统计;2)观察周期很长,某些云系统的潜在故障发生周期甚至需要几年;3)如果采用实验仿真,需要人为定期注入故障进行观察统计,这在某些商业云系统中很难被许可,观察的数据也可能难以覆盖实际故障集合。所以本文只是利用形式化方法针对提出的可用性模型进行验证。
3.1 可用性评估指标
本文不但考虑了存在PM 可用的概率,即至少存在一个可用PM,而且为了满足批量任务的部署需求,通常需要考察存在至少K个计算资源的概率PK。因此主要考察以下两个指标。
1)至少存在一个可用PM的概率。
直接计算至少存在一个可用PM 的概率较为复杂,可以利用不存在可用PM的概率间接求解。

2)至少存在K个可用PM的概率。

其中:S 是指任意状态;Nhot、Nwarm、Ncold是指处于状态S时对应的可部署的hot PM、warm PM和cold PM的数量。
3.2 结果与分析
本文采用的Markov 过程建模是一个理论模型,对于任意给定的目标系统,通过改变模型中的参数均可通过推导得到可用性的分析结果,实例不具有唯一性。因此可以任意选取一个私有云计算系统实例进行分析。假设该系统具有30 个hot PM 计算资源、20 个warm PM 计算资源和20 个Cold PM 的IaaS 系统。借鉴文献[9-10]的参数设定,假定hot PM、warm PM 和cold PM 平均部署时延的数学期望分别为0.02 h、0.05 h 和0.2 h,PM 平均释放时间均为0.2 h,故障时间间隔分别为100 h、200 h 和400 h。采用Huang 方法[8]得到系统默认参数如表1 所示。因为本文模型包含大量的参数,各个参数的取值都对可用性的分析有很大的影响,本文将对参数依次进行分析,来验证各个参数的影响。为了简化计算,提高求解效率,本文利用Eclipse Bio-PEPA Plugin工具包辅助求解。

表1 本文模型默认取值Tab.1 Default values of proposed model
1)至少存在一个可用PM的概率。
由式(8)可得当参数取值如表1 所示时,其中不可用状态有21×21=441 个,可用性的值为0.955 2。当改变Nhot、Nwarm、Ncold的值时,得到Pavail的变化如图5所示。
如图5 可见,随着hot PM、warm PM 和cold PM 数量的增长,可用性逐渐增加,并且cold PM 的趋势更为陡峭。因为当cold PM 被调用时已经没有其他可用的资源,如果cold PM 不足将直接进入不可用状态,因此cold PM 数量影响较大。对于Hot PM 和Warm PM 而言,当它们数量不足时,还可以继续调用Cold PM,因此对最终进入不可用状态的影响并不显著。
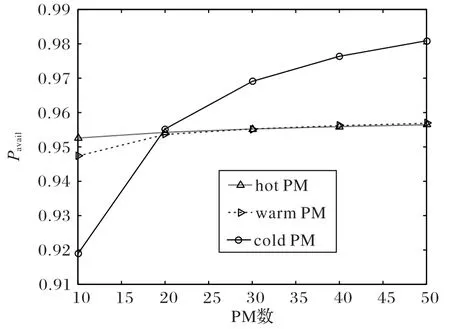
图5 PM数量对可用性的影响Fig.5 Impact of PM number on availability
当改变各关键参数λh、λw、λc、φh、φw、φc的值时,得到Pavail的变化如图6所示。
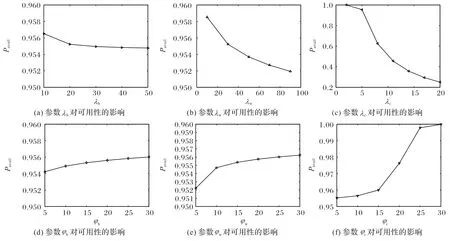
图6 PM的变迁速率对可用性的影响Fig.6 Impact of PM transition rate on availability
当λh、λw、λc等变迁速率加快时,可用性Pavail呈下降趋势,原因主要是变迁速率加快等于单位时间内需要部署PM数量增多,等价于负载压力加大。因为在本实例中PM 数量较少,Pavail会逐渐降低,尤其是λc变迁速率加快时如果没有充足的PM 将快速进入不可用状态。此外还以PM 成功释放的变迁速率为例分析了φh、φw、φc等关键参数对可用性的影响,随着变迁速率的增长,单位时间内有更多完成任务的PM 可供调度和部署任务,因此加快PM 的执行速率有利于提升云计算系统的可用性,尤其是φc的影响更为明显,因为根据调度关系没有充足的cold PM 意味着直接进入不可用状态,cold PM 执行速率的提升等价于更多备用的PM 可用,降低了进入不可用状态的概率。
2)至少存在K个可用PM的概率。
最终考察至少存在K个可用PM 的概率,以便可以部署超级任务或者批量任务。如图7 可见,存在K个可用PM 的概率逐渐降低,即随着同时需要的PM 数量的增加,PK的概率逐渐减小,原因在于PM 失效问题的存在以及部分PM 可能已经被部署使得可用的PM 数量减少。因此应该对批量任务一次性需要PM 的数量事先进行分析,以保证可以达到系统规定的可用性。
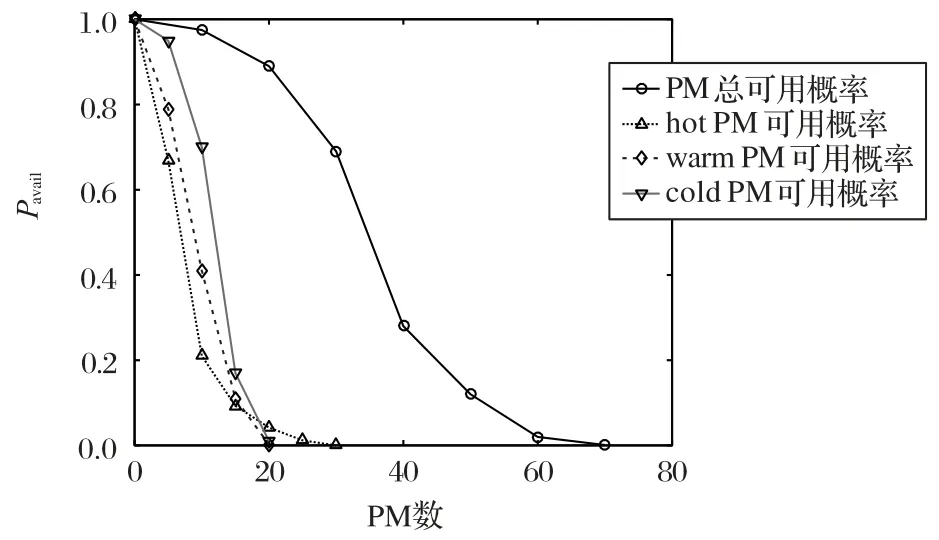
图7 至少存在K个可用PM的概率Fig.7 Probability of existing at least K PM available
4 结语
针对现有IaaS 可用性模型难以分析多个可用PM 概率的问题,本文提出了一种基于Markov 过程的IaaS 系统可用性分析方法。结合PM 调度过程建立了可用性分析模型可以分析至少存在一个可用PM的概率以及至少存在K个可用PM的概率。实验结果显示增加PM 尤其是cold PM 的数量有助于提升可用性。本文的研究没有考虑任务排队带来的影响,在后续的研究工作中,将结合任务排队等更多影响因素分析云计算系统可用性的关键影响因素。

