基于FEM和正交试验的茶园修剪机刀片的优化

易文裕,王 攀,庹洪章,卢营蓬,余满江

(1.四川省农业机械研究设计院,成都 610066;2.农业部丘陵山地农业装备技术重点实验室,成都 610066)

0 引言

树枝修剪是茶树等经济类树木种植综合管理中的重要环节,切口质量的好坏对经济作物的产量和质量具有直接的影响[1-2]。园艺学对树枝剪切的要求是沿着树枝的横截面剪切,切口平整以利于树枝断面愈合[3],而目前国产小型绿篱机作业过程中大多存在树枝切口不平整、刀片易卡死等问题,因此对小型绿篱机的刀具进行优化研究具有重要意义。

目前,国内外对刀片的研究主要集中在切割作业过程中切割阻力和切割功耗等方面,传统方法实际作业中的切割力和切割功耗研究是建立相应的试验测试平台,对机具进行测试[4-5]。传统方法的优化研究,试验周期长、工作量大、成本较高,而采用数值模拟方法对刀片切割进行研究,能够根据要求建立不同的分析模型,周期短、成本低,可有效地提高研究效率。近年来,越来越多的研究者采用离散单元法(Discrete Element Method,DEM)及有限单元法(Finite Element Method,FEM)等数值分析方法对剪切问题进行研究[6-10]。

本文以双动刃茶树修剪机刀片剪切茶树枝为对象建立有限元仿真模型,通过改变刀片的运动参数和结构参数,探究剪切过程中各参数对峰值剪切阻力的影响规律,建立峰值剪切阻力与各参数之间的数学模型,为茶树修剪机刀片的优化提供参考依据。

1 茶树枝修剪仿真模型的建立

1.1 茶树修剪机刀片仿真模型的建立

双动刃茶树修剪机在修剪茶树枝的作业过程中刀片的多组刃口同时对多根茶树枝进行剪切作业,根据FEM建模的简化原则对茶树修剪刀具进行简化,取刀片的一组刃口作为分析对象建立刀片三维模型,如图1所示。刀片刃口的角度为45°,材料选用65Mn钢,其相关参数如表1所示。

图1 刀片三维模型Fig.1 The 3D model of blade

表1 刀片模型相关参数Fig 1 The related parameters of cutter

该茶树修剪机修剪茶树枝属于茶树修剪类型中的轻修剪,根据实地测量,轻修剪过程中被修剪的茶树枝直径为2～5mm,其中3～4mm的茶树枝居多,因此在建模过程中将茶树枝简化为3.5mm的等截面圆柱体。茶树修剪机刀片在剪切茶树枝的过程中刀片与树枝之间的静摩擦因数为0.28,动摩擦因数为0.2。茶树枝的相关物理参数如表2所示,绿篱机刀片剪切茶树枝模型如图2所示。

表2 树枝模型相关参数Table2 The related parameters of the tea branch

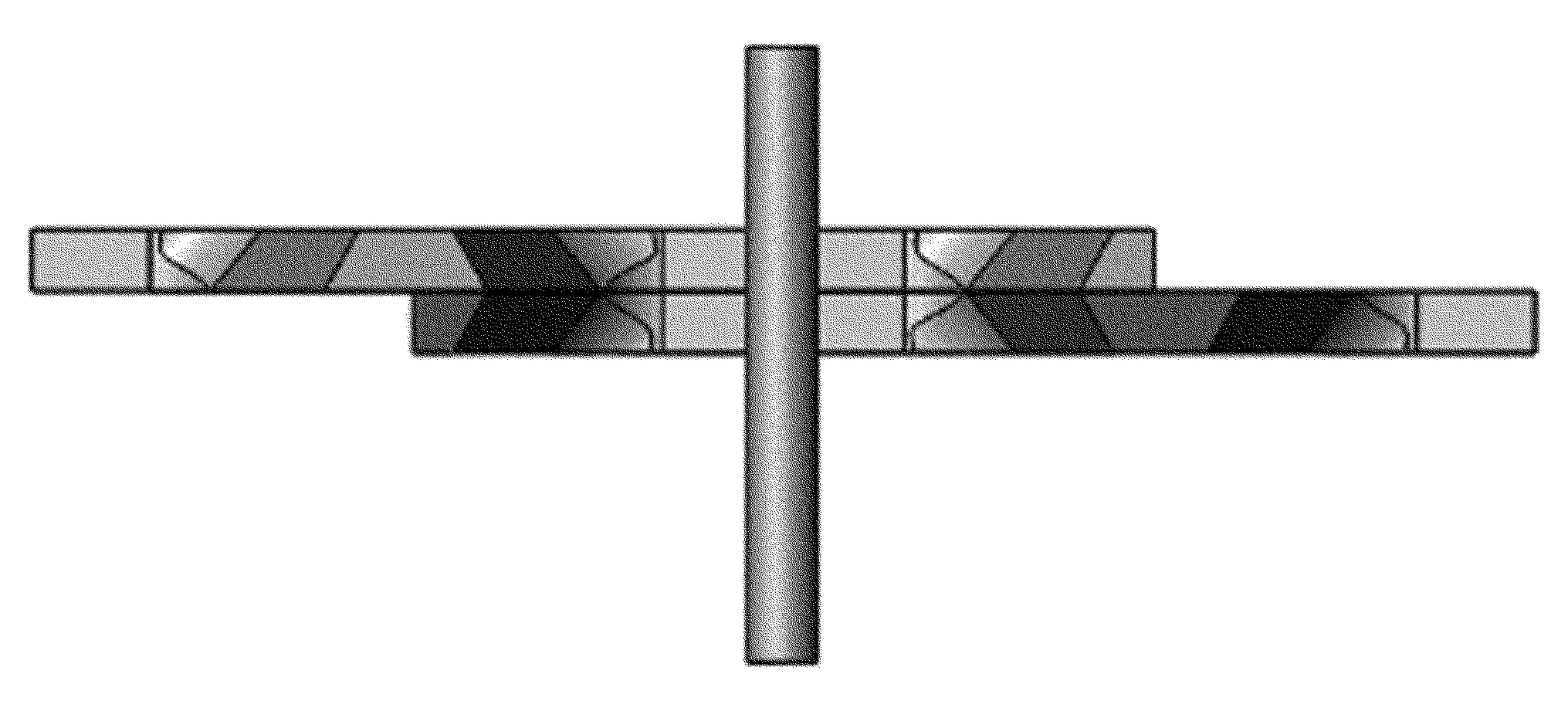
图2 刀片剪切茶树枝模型Fig.2 Model of the blade sheared the tea branch

1.2 仿真模型相关参数的确定

综合考虑树枝的各向异性、连续性及线弹性等特征,选择ANSYS/LS-DYNA中线弹性正交各向异性材料模型(orthotropic_elastic)作为茶树枝的模型,刀片模型选用刚性体(Rigid)模型。刀片与茶树枝之间的接触类型定义为侵蚀面面接触,对刀片修剪茶树枝模型进行网格划分,如图3所示。考虑到修剪过程中茶树枝的生长状态,将茶树枝模型的底面进行全约束;对上下两个刀片施加方向相反且均沿茶树枝径向的1.12m/s的速度载荷,刀片的其余方向进行全约束设置,上下两个刀片之间的间隙为0.06mm。

图3 刀片剪切茶树枝FEM模型Fig.3 The FEM model of the blade sheared the tea branch

2 茶树枝修剪的仿真与试验

2.1 刀片剪切茶树枝过程分析

刀片剪切茶树枝过程如图4所示。为清晰地表达茶树枝被剪切过程,部分图形中将刀具隐去。如图4(a)所示,当t=0s时,刀片尚未与茶树枝接触,此时茶树枝未受到外力作用;如图4(b)所示,当t=0.007 5s时,刀片刃口与茶树枝的开始接触,在刀片刃口的挤压下,茶树枝所受到的应力超过其屈服强度,茶树枝开始被破坏;如图4(c)所示,当t=0.01s时,刀片完成对茶树枝的剪切过程,被剪切下来的茶树枝在刀片的带动作用下偏离原来位置。

(a) t=0s

2.2 刀片剪切茶树枝仿真结果分析

刀片剪切茶树枝过程中剪切功率如图5所示。在0～0.007 5s的时间内,刀片未与茶树枝接触,所受阻力为0,此时剪切功率为0;在0.007 5s刀片开始受到茶树枝的剪切阻力,产生剪切功率;在0.007 5～0.010s过程中,随着刀片刃口与茶树枝接触面积的不断增大,阻力逐渐增大,剪切功率逐渐增大,峰值剪切功率为21.140W,峰值阻力为8.350N。

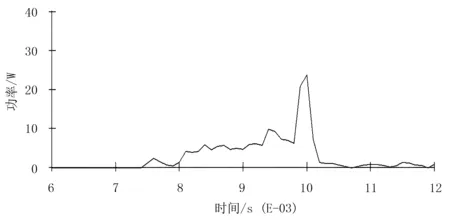
图5 剪切过程功率变化Fig.5 Power change during the shear process

2.3 刀片剪切茶树枝仿真与试验对比分析

选取5根粗细基本一致且直径为3.5mm左右的茶树枝进行单根连续剪切试验,茶树修剪机刀片剪切速度约为1.12m/s,上下刀片间隙约为0.06mm。采用APN1211E-U功率分析仪(见图6)记录剪切过程的功率变化,功率曲线如图7所示。在未开始剪切茶树枝之前,绿篱机空运行的峰值功率为185W左右,剪切直径为3.5mm茶树枝的过程中其峰值功率表为205W左右,剪切茶树枝的峰值功率约为20W。仿真结果与试验结果误差为5.7%,验证了仿真模型的准确性。

图6 剪切功率测试Fig.6 The test of shear power

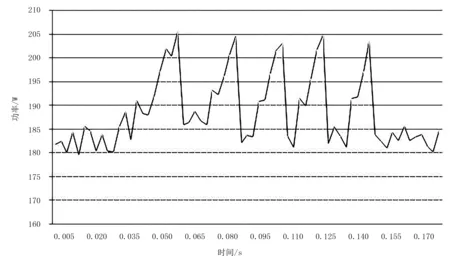
图7 连续修剪单根茶树枝功率变化曲线Fig.7 Power curve of the cut a single branch continuous

3 基于FEM与正交试验的刀片优化

3.1 二元二次回归正交试验

利用上述FEM仿真模型,针对刀片间隙和剪切速度进行正交试验,分析刀片间隙和剪切速度对刀具剪切茶树枝峰值阻力的影响,以完成对茶树修剪机刀具的优化。

综合考虑刀片的耐磨性、强度及可靠性等因素,刀片间隙选择为0.01～0.1mm,剪切速度范围选择为0.65～1.55m/s。

设计二元二次回归正交组合试验方案,其因子编码表如表3所示。其中,z1为刀片间隙,z2为刀片剪切速度,采用FEM数值分析法对刀片剪切茶树枝过程进行仿真,二元二次回归正交组合试验设计方案、结果及计算分析如表4所示。

表3 二元二次回归正交设计因子编码表Table 3 Binary quadratic regression orthogonal design factor coding table

表4 二元二次回归正交组合设计试验方案、结果及计算分析表Table 4 Test scheme and result and calculation analysis of orthogonal combination design of binary quadratic regression

根据表4得到峰值阻力、刀片剪切速度和刀片间隙的回归方程为

P=6.7020-902.0246z12+1.4357z22+142.2163z1-

3.8348z2-22.727z1z2

经检验方程显著性和拟合性均满足要求。

3.2 刀具优化

根据峰值阻力方程及刀片剪切速度和刀片间隙的设计要求,利用MatLab的全局最优算法求解,得到峰值与刀片剪切速度和刀片间隙的三维曲面图,如图8所示。

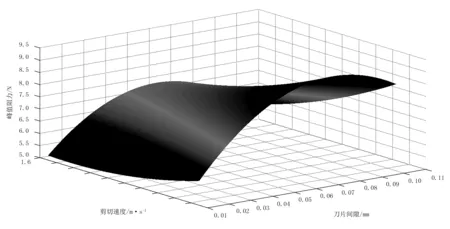
图8 峰值阻力与剪切速度和刀片间隙的三维曲面图Fig.8 Hump drag and shear velocity and blade clearance of three-dimensional surface

结果表明：随着刀片剪切速度的增加,峰值阻力逐渐减小;峰值阻力随着刀片间隙的增大先增大后减小。当刀片剪切速度为1.414 7m/s、刀片间隙为0.01mm时,峰值阻力最小为5.160 7N。

4 结论

采用FEM数值分析方法建立了茶树修剪机刀片剪切茶树枝过程的仿真模型,并通过功率测试试验验证了该模型的准确性。在此基础上,运用正交试验和FEM数值分析方法对刀片进行了优化设计,研究结果为绿篱机刀片的改进设计提供了理论支撑,也可为降低绿篱机剪切峰值阻力及提高产品耐磨性等相关研究提供借鉴。