林分结构多样性研究进展*
赵中华 惠刚盈
(中国林业科学研究院林业研究所 国家林业和草原局林木培育重点实验室 北京 100091)
20世纪90年代以来,生物多样性与生态系统功能(biodiversity and ecosystem function,BEF)之间的关系受到科学界广泛重视(马克平, 2013),维持和提高生物多样性成为国内外研究热点之一。森林生态系统在维持生态安全、维护人类生存发展的基本条件中具有决定性和不可替代的作用,保护并维持森林多样性是森林可持续经营的重要目标。根据研究尺度不同,生态系统多样性可划分为α多样性、β多样性、γ多样性和δ多样性(MacArthur, 1965; Whittaker, 1972)。对于森林生态系统而言,α多样性用于林分水平上的多样性分析,β多样性用于比较不同林分的差异,γ多样性和δ多样性则用于更大尺度上的多样性分析,如在景观水平上(Lähdeetal., 1999)。森林结构体现林木个体(结构要素)及其属性(种类、大小、分布)的连接方式,是森林的重要特征。林分结构是森林结构的基本单元,是森林发展过程,如更新方式竞争、自然稀疏和经历干扰活动的综合反映,是森林经营与分析中的重要因子,也是实施森林经营活动的具体对象(O’Haraetal., 1996),开展林分结构研究可帮助人们了解森林的发展历史、现状和生态系统发展方向(Staudhammeretal., 2001; Franklinetal., 2002),提高林分结构多样性和复杂性,被认为是实现森林生态系统生物多样性维持和增加的基础(Franklinetal., 2002; Oliveretal., 1996; Leietal., 2009; Valbuenaetal., 2012)以及精准提升森林质量的有效途径。
林分结构多样性是不同结构属性相对丰富程度和均匀性的基本度量,体现林分在水平和垂直2个方向上的多样性和复杂性,不仅与群落内物种丰富程度和个体大小有关(Buongiornoetal., 1994),而且与林分的垂直结构关系密切(MacArthuretal., 1961; Oliveretal., 1996)。雷相东等(2002)从是否考虑林分中树木位置出发,分类综述了林分结构多样性指标研究进展,认为基于林分结构的多样性指数易与经营直接相关的因子(如断面积、密度和径阶分布等)联系起来,可通过营林活动来维持生物多样性。经过近20年的研究,林分结构分析方法取得重大进展,先后出现了基于相邻木关系的林分空间结构表达方法(惠刚盈等, 2007)、林分结构二阶特征分析方法(Pommereningetal., 2011; Huietal., 2014)以及各种与林木属性、尺度相关的标记特征分析方法,这些方法丰富了林分结构多样性研究内容,使林分结构与生态过程相结合成为可能。Gadow(1999)、Gadow等(2012)和Pommerening(2002; 2006)研究认为,林分水平上的结构多样性可从树种多样性、树木位置和林木大小多样性3方面进行描述和刻画,本研究借鉴这一方法,从林分结构组成多样性、林木大小分化多样性和林木空间分布多样性3方面对林分结构多样性研究进展进行系统梳理和总结,探讨林分结构多样性与林分结构复杂性的关系,分析未来研究重点,以期为进一步构建既能体现林分结构三维特征,又能与森林经营活动、森林调查、规划体系相结合的新指数,指导开展森林经营活动,切实提高森林质量提供有益参考。
1 林分结构组成多样性
1.1 林分组成属性多样性
林分结构组成多样性常以林分组成属性为基本统计单位,以植物群落学中的α物种多样性指数为基础来表达。群落生态学中的物种多样性表达方法目前已经发展了30多种指数,是生物多样性中研究最早、最活跃的层次。林分结构组成多样性的度量常以林分中各树种比例为变量,运用物种多样性指数计算林分树种组成结构多样性,如Shannon-Wiener指数、Pielou均匀度指数、Simpson指数和Margalef指数等。当用断面积、林下植被、枯立(倒)木或其他结构分类变量代替树种时,可反映对应林分组成结构属性的多样性特征,如胸高断面积组成多样性(Hollandetal., 1994; Buongiornoetal., 1994; Volinetal., 1996)、叶层多样性指数(MacArthuretal., 1961)以及枯立(倒)木多样性(Dewaltetal., 2003; Bachofenetal., 2001; Svenssonetal., 2001; Sullivanetal., 2001; Van Den Meersschautetal., 1998; Tyrrelletal., 1994; Spiesetal., 1991)等。表1以树种组成为例说明了常用林分组成结构多样性指数的计算方法。基于生物多样性指数的林分组成结构多样性与物种多样性相似,是一个数值,便于比较不同林分类型的组成多样性大小。多样性应该是组成因子丰富程度与均匀性的结合,但现有生物多样性指数有的侧重于表达组成因子的丰富程度,如丰富度指数,有的则侧重于表达物种分配的均匀性,如Pielou均匀度指数,缺乏既可表达组成因子丰富程度又能表达物种分配均匀性的指数。雷相东等(2002)对基于物种多样性指数的林分组成结构多样性指数的优点及在应用中存在的问题做了详细综述,本研究不再赘述,但需要说明的是,本研究并未将胸径多样性和树高多样性归于林分组成多样性,而是将其作为大小分化多样性指标。

表1 常用林分组成结构多样性指数(以树种组成为例)Tab.1 Commonly used stand composition diversity indices(species composition as example)
1.2 基于相邻木关系的林分组成结构多样性
基于相邻木关系的林分组成结构多样性指数经历了不断的发展过程(表2)。Pielou(1961)基于最近相邻木关系提出了分隔指数(segregation),用于描述群落中物种的种间隔离关系; 尽管Pielou分隔指数计算没有运用林木相对坐标,但其描述了群落中2个种群个体的相对位置分布关系,即2个树种在群落中是随机分布、吸引还是排斥。Füldner(1995)认为Pielou分隔指数仅适用于分析树种随机分布混交林的种间隔离关系,对均匀和团状分布的种群易造成不合理描述。Gadow等(1993)提出了基于3株相邻木关系的混交度概念,该指数对种类较多的混交林树种隔离程度表现出较好区分度,在一定程度上也体现了林分中树种组成多样性。惠刚盈等(2001)认为,选择4株相邻木能更好表达混交度的林学意义,并给出了林分整体平均混交度的计算方法以及林分中树种混交度的表达方法。为进一步增强混交度对林分树种多样性的表达能力,汤孟平等(2004)提出了树种多样性混交度概念,惠刚盈等(2007)对林分平均混交度计算公式进行了修正,其方法均是将结构单元中树种个数作为权重参与到林分平均混交度计算结果中,不仅可体现林分中树种分隔情况,而且能体现林分树种组成多样性。此后,Hui等(2011)又在林分平均混交度修正基础上提出了基于相邻木关系的树种空间多样性指数(TSS),并将其与常用林分树种组成结构多样性指数进行对比,体现了很好的区分度。汤孟平等(2012)对混交度进行了改进,在此前修正的基础上,将Simpson指数引入结构单元,用于描述树种分布均匀性,提出了全混交度概念,并与简单混交度、修正林分平均混交度、树种多样性混交度和树种空间多样性指数等进行比较,给出了各种混交度间的关系,认为现有林分结构多样性指数对林分结构的描述存在片面性,各种混交度计算方法都是对简单混交度的修正,既有联系又有区别。

表2 常用基于相邻木关系的林分组成结构多样性指数Tab.2 Commonly used stand composition diversity indices based on near neighbor relationship
2 林木大小分化多样性
林木大小分化多样性以林木个体树干粗细、高低以及树冠大小为指标表征林木大小分化程度。胸径数据收集相对简单、准确,是许多永久性样地的测量基础(Ackeretal., 1998),由此发展了许多表达林木大小分化程度的多样性指标,如大小变异系数、Gini系数、胸径分布偏度、大小分化度等。这些指标除了能用胸径作为比较因子外,还可用树高、冠幅、断面积等。也有许多学者采用Shannon-Wiener指数和Simpson指数分析林木胸径分布,称为大小多样性(Wikstrometal., 2000; Gove, 1998; 白超等, 2016)(表3)。Buongiorno等(1994)认为林木大小多样性是叶面高度多样性的一个很好指标,因为林木大小多样性等同于冠层高度和叶面分布多样性。林木高度大小变异反映了林分在垂直方向上的变化,常用来表达林分结构多样性; 与林木高度相关的最简单属性是林层高度,可以指示演替阶段(Kappelleetal., 1996)、林层数目(Spies, 1998)和林分生物量(Meansetal., 1999)等; 复杂的树高结构也可能包含各种树龄和物种,从而为野生动物提供多种微生境(Zenner, 2000)。此外,还有一些研究将树叶垂直排列、大树数量、冠层间隙和冠层覆盖变异程度等作为林木大小分化多样性的指标,如Ziegler(2000)和Tyrrell等(1994)以冠层在林隙中的比例、林隙的平均大小以及大小等级之间的差距分布作为表达林分结构的重要属性。
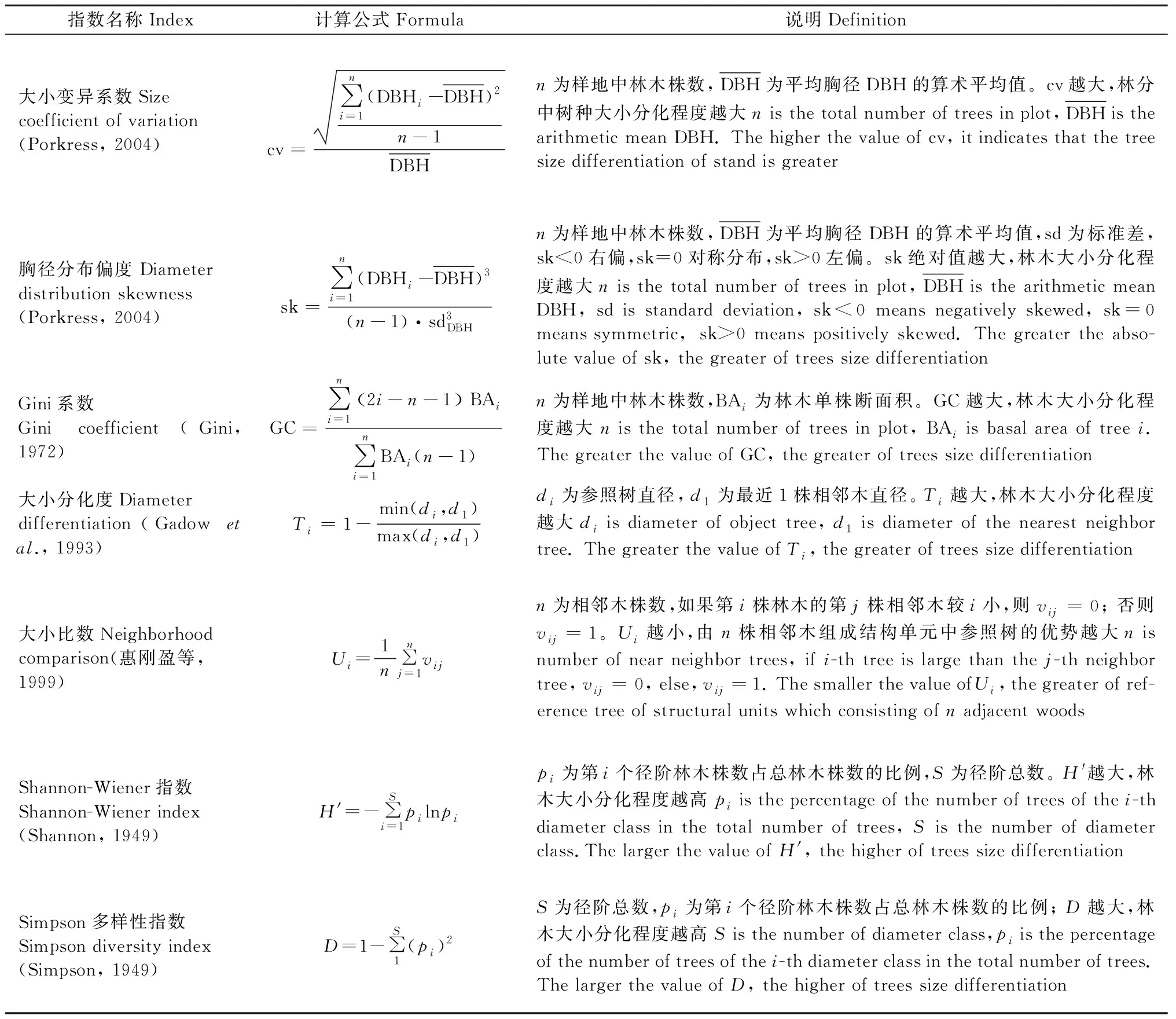
表3 常用林木大小分化多样性指数(以林木胸径大小为例)Tab.3 Commonly used stand size differentiation diversity indices(tree diameter size as example)
3 林木空间分布多样性
林木空间分布多样性的实质是林木在水平空间上的位置分布格局多样性,即由于环境异质性、林木间竞争、种子传播机制等多种因素作用下导致的林木分布位置关系。林木水平分布格局通常可分为均匀分布、随机分布和团状分布3种情况,在传统生态学研究中已经发展了大量关于林木分布格局的判定方法,如样方法和无样地法,常用的指数有方差均值比(Blackman, 1942)、Peilou非随机指数(Peilou, 1959)、负二项指数、扩散指数、丛生指标、聚集指数(Clarketal., 1954; 兰田玉等, 2003)等,但这些方法或指标大多为判定林木分布格局类型的方法。Riply(1977)提出了点格局分析方法,后来经Diggle(1983)、Pettiinen等(1992)、Stoyan等(1998)、Illian等(2008)的发展,将点格局方法与尺度变化相结合从而体现林木空间分布格局多样性。
3.1 点格局分析方法
点格局分析方法以植物个体的位置坐标为基础数据,将每个个体视为二维空间上的一个点,通过对空间上任意2点间的二阶特征乘积密度与随机分布状态下的值进行比较,判断2点间是否独立存在或有某种联系,常用的方法有Ripley’K函数、基于Ripley’K函数的L-函数、O-ring统计方法及双相关函数。Ripley’K函数是以点格局中某个特定点为中心、以r为半径的圆中存在点数的概率计算出来的统计量(Ripley, 1977),其函数形式见表4。由于Ripley’K函数随尺度r增加自身以r2速率增加,即二次函数形式增加,会产生尺度累积效应,从而影响判别结果。为消除尺度累积效应,产生了K(r)变形后的L-函数(Besag, 1977)和O-ring统计方法(Conditetal., 2000; Wiegandetal., 2013),后者以抽样点为中心,用圆环替代Ripley’sK(d)函数中的圆圈,计算环内点的平均数目,从而可孤立特殊的距离等级,消除尺度累积效应。双相关函数g(r)表达的是实际中发现2个点的概率密度与期望密度的比值,2个点的概率密度为二阶特征乘积密度,而期望密度可认为是完全随机分布格局中发现被距离r分隔的2个点的概率(Gavrikovetal., 1995)(表4)。单变量的Ripley’K函数、O-ring统计方法和双相关函数能够分析林木位置的分布格局,而双变量函数能够分析2个变量的相互关系。点格局方法在林木分布格局和林木相关性分析中运用越来越广泛,但在对其进行应用时需要考虑2个问题: 一是选择合适的零模型,因为零模型决定着现实树种空间分布格局是否偏离随机分布状态以及偏离的程度(Wiegandetal., 2013); 另外一个重要因素是对数据要求较高,需要林木的相对位置坐标,并进行边缘校正; 此外,点格局方法计算过程相对复杂,需要专门的软件或代码支持。角尺度判断林木分布格局实质上也是一种点格局方法,不仅可用图形来描述林分中林木分布,而且还可用均值或显著性检验方法来判断林木分布格局(惠刚盈等, 1999; Zhaoetal., 2014),该方法并不一定需要林木定位坐标数据,通过简单的辅助工具即可获得相关数据。

表4 常用点格局分析函数Tab.4 Commonly used point process pattern function
3.2 标记二阶特征分析
点格局分析方法对林木位置分布格局进行描述,体现了林木位置随尺度变化的多样性。而在现实林分中,被认为是点的林木除了位置属性外,自身还带有一些属性,如树种、胸径、树高、冠幅、活立木和枯死等, 将林木自身定性或定量的属性“标记”在位置坐标上,分析这些具有自身属性的点的空间分布特征方法被称为标记点格局(Gavrikovetal., 1995; Pommereningetal., 2011; Wiegandetal., 2013)或标记二阶特征。常用的标记特征函数有标记双相关函数 (Penttinenetal., 1992; Pommerening, 2000)和标记变异函数 (Stoyanetal., 1998; Pommereningetal., 2013),这2个函数可用下式表示:
(1)
式中:x1和x2为观察窗口W中的任意点;kh为Epanechnikov核函数;A(Wx1∩Wx2) 为整个观察窗口的面积;t1(m1,m2)为测试函数;c为标准化项。
标记双相关函数与标记变异函数的区别主要在于测试函数和标准化项不同(Pommereningetal., 2013)。运用标记双相关函数和标记变异函数可对林木不同的定量或定性属性进行不同尺度上的变异描述,从而体现林木空间分布多样性,能够对森林结构提供更多的生态学解释,但该函数描述不同树种的相关性时只能成对比较,对于复杂的混交林而言,需要剔除其他树种,结果解释可能是片面的。Pommerening等(2011) 基于标记相关函数(Diggle, 2003; Illianetal., 2008)的构造原理,以Gadow(1993)提出的简单混交度和大小分化度作为测试函数,以林分期望混交度和期望大小分化度作为标准化项,构造了标记混交度和标记大小分化二阶特征函数,用以描述林分中树种混交和林木大小分化程度随尺度变化的特征。标记混交度和大小分化二阶特征函数如下:
(2)
(3)
式中: EM和ET分别为期望混交度和期望大小分化度;x1和x2为观察窗口内的任意2个点;kh为Epanechnikov核函数;A(Wx1∩Wx2)为Wx1和Wx2相交面积。
标记混交度和大小分化二阶特征函数曲线实质是林分相应尺度上标记指标观察值与期望值的距离,结果可解释为林分中不同树种和大小林木随尺度变化的分布情况,同时可根据曲线远离期望值的程度判断相应尺度上树种或大小分布格局的强度,但其结果不能体现林分树种组成的丰富程度和林木大小的变异程度。标记函数对具体的生态学过程和假说具有一定分析和解释能力,如Wang等(2017)将樟子松(Pinussylvestrisvar.mongolica)天然林中的枯立木和活立木作为标记特征,利用标记二阶特征函数分析了二者的关系,并采用负密度效应解释了这一格局形成的原因。
4 林分结构多样性与复杂性
林分结构多样性与林分结构复杂性既有联系又有区别,不能将二者截然分开,在实际工作中林分结构多样性常作为林分结构复杂性的替代指标。林分结构属性种类繁多,研究者可能会根据关注重点而选择不同的结构属性来描述多样性; 单一结构属性的量化仅能描述相应属性的多样性,如运用Shannon-Wiener指数量化单个属性,实际上其仅仅量化了许多可能属性中的一个(Goveetal., 1995; Buongiornoetal., 1994)。McElhinny 等(2005)认为,林分结构复杂性是不同结构属性数量以及每个属性相对丰富程度的基本度量,结构复杂性优先于结构多样性。林分结构复杂性必然涉及许多不同属性(变量)之间的相互作用,需要复杂的多元分析进行定量表达,除了用林分结构多样性指标替代外,还设计了一些指标进行林分间结构差异的比较(Watsonetal., 2001; Koop, 1995; Newsomeetal., 1979)。一类是基于结构属性累加或赋权重的方法,即选择一组林分结构属性,根据结构属性分别赋予不同的分值或权重,然后利用可加性或平均值法来表达林分结构复杂性(Burgmanetal., 2001; Ackeretal., 1998; Koopetal., 1995; Staudhammeretal., 2001),如Barnett(1978)、Newsome等(1979)将林分不同层次的盖度进行赋值来评价林分结构复杂性; Van Den Meersschaut等(1998)选择18个指标详尽的指数来描述比利时森林生物多样性。另一类是基于结构属性交互作用的方法,将林分结构属性以非线性的方法相结合(Burgmanetal., 2001; Zenner, 2000; Lietal., 2012),如Holdridge(1967)提出的HC指数,将树高、断面积、密度和上层物种数量在一起表达结构复杂性; Jaehne等(1997)将物种组成、直径、树间距和冠幅变异相乘,提出SD指数来表达林分结构复杂性。Zenner(2000)基于树高与树木空间位置之间的相互作用构建了一个结构复杂性指数SCI,将林木位置和树高视为三维数据点,其中x、y坐标表示水平位置,z坐标表示高度,将3个相邻三维数据点连接起来形成一个不重叠的三角形网络,SCI被定义为这些三角形的表面积总和除以三角形所覆盖的水平面积。SCI量化了林木位置与树高的关系,具有有限的实用价值,因为其要求精确确定每株树的位置和高度。以上方法构建的指数尽管在一些方面表达出了林分结构复杂性,但由于结构属性多样性、林分结构、功能与组成间的相互依赖性(Franklinetal., 2002; Ferrisetal., 1999; Noss, 1990)、林分结构属性选择的主观性等因素,这些指标仍被认为是不全面的; 此外,将不同量纲的结构属性进行相加或相乘,其合理性值得商榷。
5 讨论与展望
林分结构变异性是林分潜在生物多样性的一个重要因素(Uutteraetal., 1995),目前已经发展了许多林分结构多样性指数,也有许多方法开始探讨将林分结构多种属性进行归类,如McElhinny等(2005)将林分结构属性进行分类,总结了相应林分结构属性的多样性表达方法。本研究借鉴Gadow(1999)、Gadow等(2012)和Pommerening(2002; 2006)的划分方法,从结构多样性的组成多样性、大小分化多样性和空间分布多样性3方面对现有林分结构多样性进行梳理,并对林分结构多样性与林分结构复杂性的关系进行探讨。也有建议将林分结构属性从林分的水平结构、垂直结构和空间结构3方面进行分类,探讨林分结构多样性,这是一个很好的分类方法,但该方法的实质与本研究的分类方法是一致的,林分的水平结构包括胸径、冠幅等指标,垂直结构反映了林分的分层结构,如树高、树叶垂直排列、大树数量、冠层间隙和冠层覆盖变异等,而空间结构与空间分布多样性相同,二者的主要区别仍是对属性归类的差异。林分结构是组成森林生态系统的各要素在空间和时间上的排列,是一个多维度概念(雷相东等, 2002),因此,林分结构多样性的表达也应体现林分结构的多种维度,目前尚未有很好的方法体现林分结构的多维属性,探索林分结构多样性和复杂性的表达方法仍是一项富有挑战的工作。
开展林分结构多样性和复杂性研究的最终目的是认识复杂森林生态系统的差异,帮助人们更好地理解生态过程,指导开展科学的植被管理。近年来,点格局分析方法取得了很大进展,这对于解释生态过程和生态学假说是有益的,具有巨大应用潜力,但与许多生物多样性指数类似,很难用于指导植被管理和林分结构调整。基于相邻木关系的结构参数实现了指导林分结构调整并进行了试验示范(惠刚盈等, 2007; 赵中华等, 2013),在应用时仅需综合考虑培育对象与相邻木的4种关系。目前已有将4个指数进行两两结合(Lietal., 2012)或多个指数进行结合(白超等, 2016)的探索,但仅限于对结构特征或微环境的描述。基于以上认识,未来还需要从以下几方面进行研究: 一是通过数学方法构建既能体现林分结构多维性又能灵敏反映林分结构差异性的林分结构多样性指标,尽可能实现林分结构多样性的量化表达,从而更加直观体现林分结构多样性; 二是在构建林分结构多样性指数时要尽可能考虑林分结构的多种属性,同时还应考虑各属性在表达林结构多样性时的权重问题; 三是在研制新的林分结构多样性指标时应尽可能与具体的经营措施相结合,使指数或模型既能体现林分结构的多样性和复杂性,同时又能在具体的经营活动中容易实现指导林分结构调整,对经营活动进行评价,最终实现增加林分结构多样性、维持和增加森林生态系统多样性的目的。

