基于组合赋权法和灰色关联度分析法的装配式建筑成本影响因素研究
杨 涛,李书卉
(1.河北水利电力学院,河北省沧州市重庆路1号 061001;2.大元建业集团股份有限公司,河北省沧州市永济东路18号 061001)
目前,装配式建筑在国内的应用日益广泛,并逐渐被应用于国家大学基础设施建设当中[1-2]。在装配式建筑应用中,直接将工程生产的预制构件,在施工现场进行装配,最终形成建筑,其具有环境影响小、施工生产效率高和建设周期短等优点,确保了该建筑类型的应用前景,截止到2020年,国内该类型建筑的比例将超过15%[3-4]。但由于目前国内尚没有针对装配式建筑的标准规范,技术体系不完善,社会认可度较低[5],限制了该类型建筑的发展。
Chang等[6]研究了装配式建筑的最优运输模式,指出如何获得最高的运输效率将直接影响整个建筑成本;王广明[8]等分析了20个省份12个代表工程的建筑成本,指出装配式建筑在成本方面较其余类型建筑存在一定的优越性;李丽红[9]对比了装配式建筑与其余类型建筑的成本,指出造成其成本较高的原因是由于吊装费用和运输费用较高。
成本是制约装配式建筑广泛应用的主要因素之一,为得出影响装配式建筑成本的主要因素,基于组合赋权法及灰色关联度分析法,构建建筑成本影响因素综合分析体系,指出最关键影响因素,为装配式建筑的应用及建筑成本的降低提供理论依据。
1 建筑成本影响因素确定
基于全面性、科学性、可操作性和层次性的原则,从参与各方因素、外部环境因素和项目本身因素3个方面建立装配式建筑成本影响因素评价体系。查阅文献,可得出影响装配式建筑的影响因素,结果见表1。

表1 总体指标体系Tab.1 Overall indicator system
基于主成分分析法对表1中的数据进行分析,得出影响装配式建筑成本的主要因素。该方法可在保证原有指标数量不变的前提下,将存在一定相关关系的指标通过线性组合的方式形成新的指标体系,该体系指标数目较少,但代表性较好,可达到降维的目的。具体步骤可参考文献[9]中的方法。
为保证每个系统层指标评价的公平性,3个系统层指标分别选择4个指标进行评价,基于主成分分析法,选择累积率高于95%的指标进行后续的影响因素评价,最终每个指标的主成分得分情况见表2。
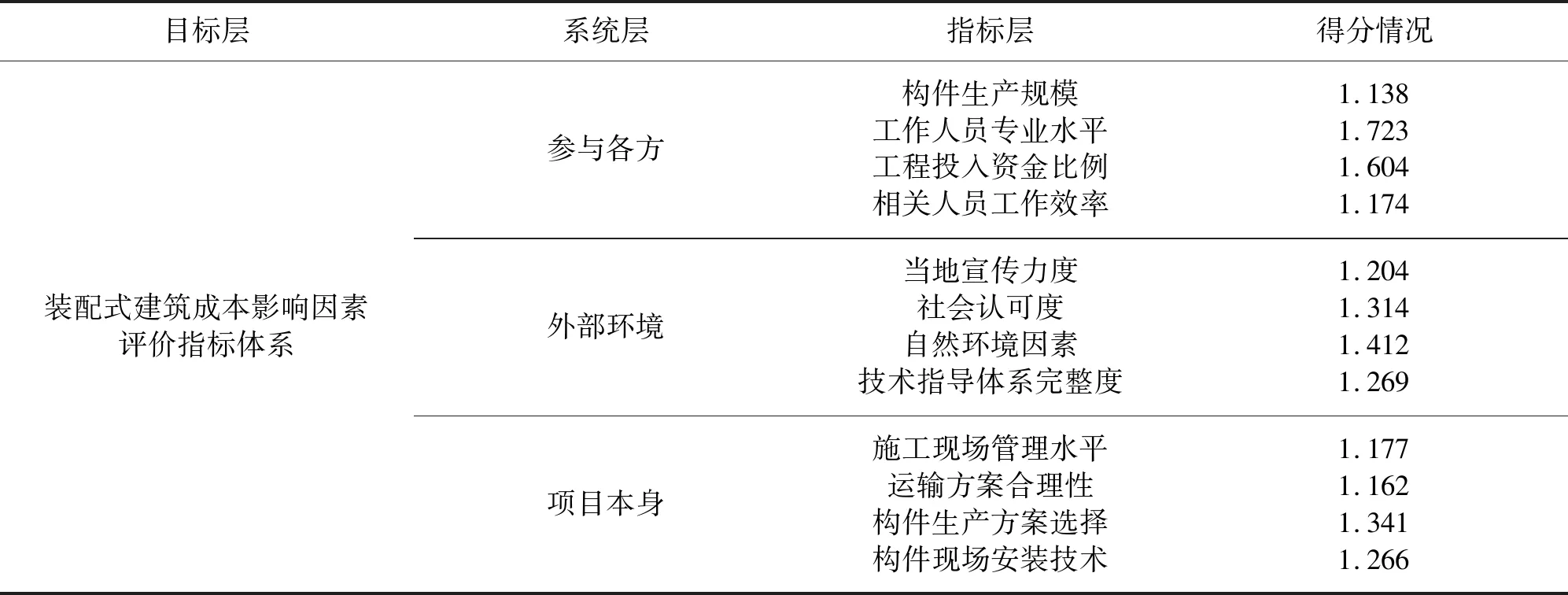
表2 主成分得分情况表Tab.2 Component score principal
在每个方面分别选择4项指标,最终构建评价体系见图1。
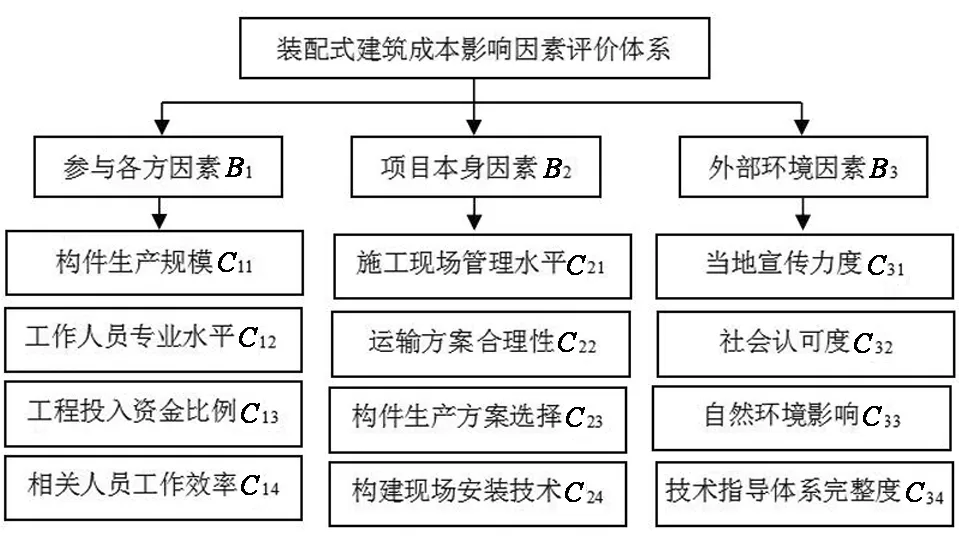
图1 指标体系构建Fig.1 Index system construction
2 评价方法确定
2.1 灰色关联度分析法
对于一个最优数列x0有若干个比较数列x1,x2,…,xn,关联系数ξxi:
(1)
式中:ρ为分辨系数,一般在0~1之间,通常取0.5;Δmin为两级最小差;Δmax为两级最大差;Δ0i(k)为各值与最优值之差。
由计算得到的ξxi,计算关联度,并以关联度的大小排序。
2.2 计算权重
2.2.1 模糊层次分析法计算主观权重
模糊层次分析法在层次分析法的基础上进行改进,得出两个因素之间的重要程度,根据重要程度,得出模糊互补矩阵,定量表达出不同指标的重要程度[10]。不同指标判断矩阵的确定可参考表3,具体计算步骤可参考文献[10]。为保证得出的模糊层次分析法判断矩阵的准确性,需对判断矩阵进行一致性系数的计算,当一致性系数小于1时,认为该判断矩阵具有一定的合理性。
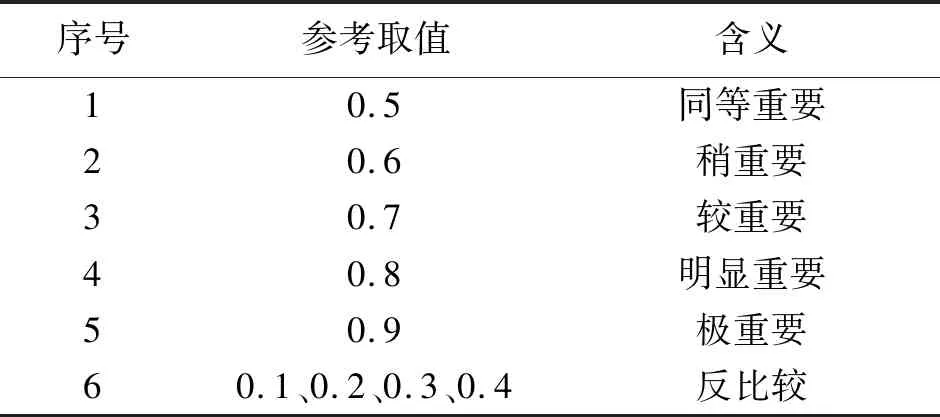
表3 指标体系判断矩阵取值参考Tab.3 Index system judgment matrix value reference
2.2.2 熵权法计算客观权重
对各项指标进行无量纲化处理,得出相对隶属度:
(2)
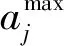
计算第j项指标的变异度:
Dj=1-Hj
(3)
式中:Dj为所求的变异度;Hj代表指标的信息熵。
计算该指标所对应的熵权重(客观权重):
(4)
式中:wbj为所求的客观权重;Dj为某项指标的变异度。根据模糊层次分析法得出的主观权重与熵权法计算得出的客观权重,得出综合权重。
2.2.3 综合权重确定
综合权重公式为
(5)
式中:wj为所求的综合权重;waj为通过问卷调查所得的主观权重;wbj为所求的客观权重。
3 实例分析
以河北省某装配式建筑实际工程为实例,根据现场调查及专家打分数据,计算得出影响建筑成本的关键因素。首先利用模糊层次分析法的原理,构建第二层指标的判断矩阵,结果见表4。由表4可知,项目本身因素的权重为0.517,远高于其余2个方面,而计算结果中的一致性系数为0.13,其值小于1,表明了该结果的合理性。
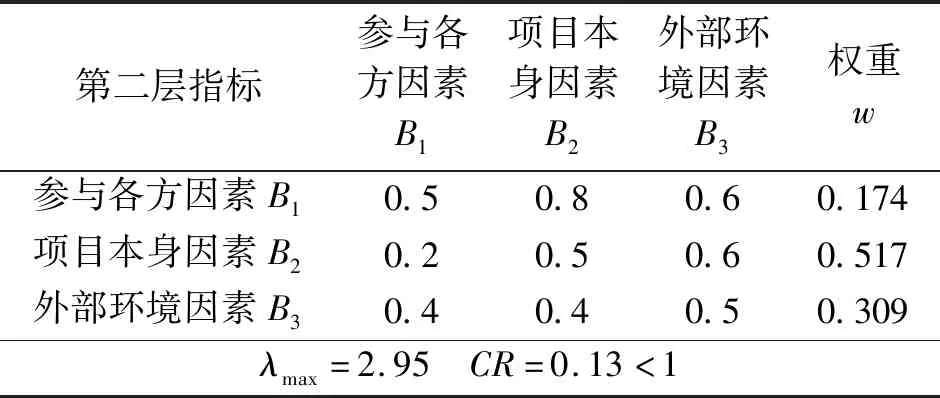
表4 第二层指标相关权重计算Tab.4 The second level indicator related weight calculation
以参与各方因素B1层次为例,建立第三层指标的判断矩阵,结果见表5。由表5中的数据,可得出参与各方因素下,4项指标的权重,同理可得出其余2个层面各项因素的权重,结果见表6。由表6中的权重计算值,结合表2中的第二层指标权重,即可得出第三层指标的最终主观权重,结果见表7。
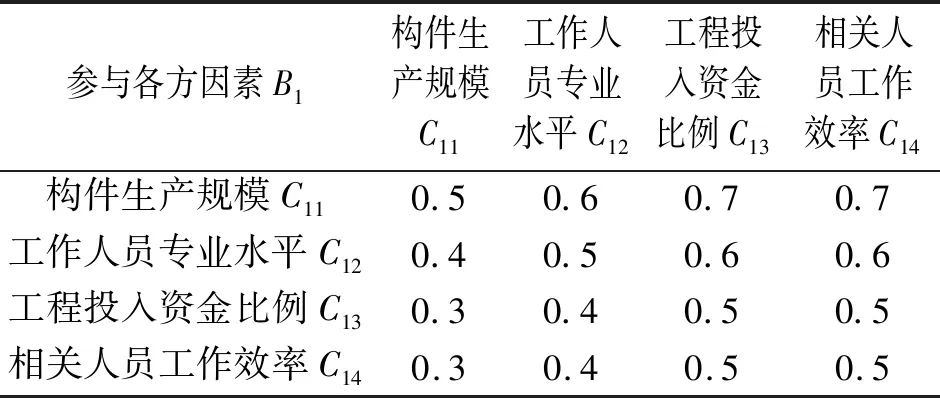
表5 第三层指标判断矩阵构建Tab.5 The third level index judgment matrix construction
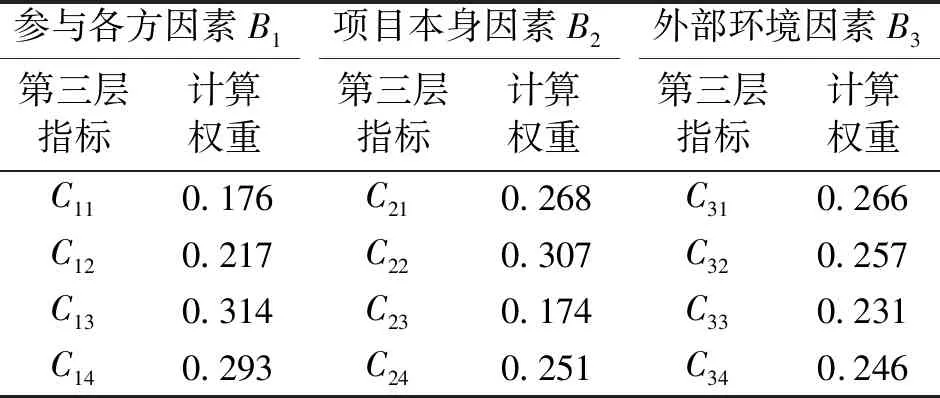
表6 第三层指标权重Tab.6 The third level indicator weight

表7 最终权重确定Tab.7 The final weight determination
确定不同指标的相对隶属度矩阵,结果见表8。熵权法计算结果基本与主观权重一致,由主观权重和客观权重,可综合得出第三层指标的初始综合权重,结果见表9。

表8 第三层指标相对隶属度矩阵Tab.8 The third-level index relative membership matrix

表9 第三层指标最终权重确定Tab.9 The final weight of the third level indicator determination
由表9中计算出的各项指标最终权重可以看出,项目本身因素对整个建筑成本的影响因素要高于外部环境因素和参与各方因素,同时主观权重、客观权重和综合权重所反应出的规律是一致的,进一步证明了权重计算方法的合理性。
由灰色关联度分析法计算每项指标的关联系数,根据表9中的指标最终权重,即可得出装配式建筑影响因素最终关联系数,结果见表10。由表10中的数据可得,12项指标对建筑成本的影响程度由大到小依次为C22>C21>C24>C34>C31>C32>C33>C23>C14>C13>C12>C11,即影响程度最大的因素为运输方案的合理性,构件生产规模为影响最小的因素,而项目本身的因素是影响装配式建筑成本最关键的层面。

表10 最终关联系数确定Tab.10 The final correlation coefficient determination
4 结语
针对装配式建筑成本较高的缺点,基于组合赋权法和灰色关联度分析法,对影响成本的因素进行了权重计算和分析,得出运输方案的合理性关联度系数达到了0.182,是影响装配式建筑成本最主要的因素。选择了12项指标建立了评价体系,在今后的研究中可建立指标覆盖率更强的体系,更加全面地分析影响装配式建筑成本的关键因素,以便在建设中提起注意。

