浮山县臣南河水库曲面体型模板设计

李若飞

（山西省水利建筑工程局有限公司，山西 太原 030000）

1 工程概况

臣南河水库位于浮山县城北5 km处的丞相河村东南河上，是一座以调蓄浮山供水工程和流域内地表水，为农业灌溉、城镇生活和工业供水的小（一）型水库，水库总库容538.56万m3。泄洪洞位于大坝桩号0+172处，与坝轴线垂直，泄洪洞进水塔底高程688.50 m，塔顶高程722.8 m，塔身高34.3 m，泄洪洞为马蹄形断面，洞径6 m。

2 模板设计要求

2.1 模板设计难点

本项目施工的难点在于泄洪洞的进水口及连接段的施工，在曲面模板的制作过程当中对模板的强度和模板体型的要求非常高，模板的设计简便易操作，同时能够尽可能节约材料。在本项目中，工程中将用到的几组外形中异形的模板，从方便施工的角度考虑，对模板选型的重要性进行说明。

2.2 水工曲面体型介绍

泄洪洞进水口由两个椭圆曲线组成，设泄洪洞进水口底部所在平面为XY面，水流方向为正X轴方向，左右边墩为Y轴，左为正半轴，垂直地面向上为+Z轴方向，XZ面垂直于XY面；图1为进口顶部结构，进口顶部椭圆曲线方程为，图 2为进口边墩，进口边墩椭圆曲线方程为

该进水口基座以及顶部皆为椭圆形设计，整体呈对称性设计。图1和图2为关键部位的三视图，对图纸中数据进行分析可得基座与壁面相切，顶部椭圆柱面与里面椭圆柱体相切。设基座的方程式为1，顶部的方程式为。式中，a、b和m、n分别表示两个椭圆方程的长轴和短轴。

图1 进水口侧视图

图2 进水口俯视图

3 建立空间坐标系

根据实际情况建立数学模型，考虑到洞口的对称性，图3为坐标系垂直俯视图，图4为坐标系Y向进水口侧视图。

图3 俯视图

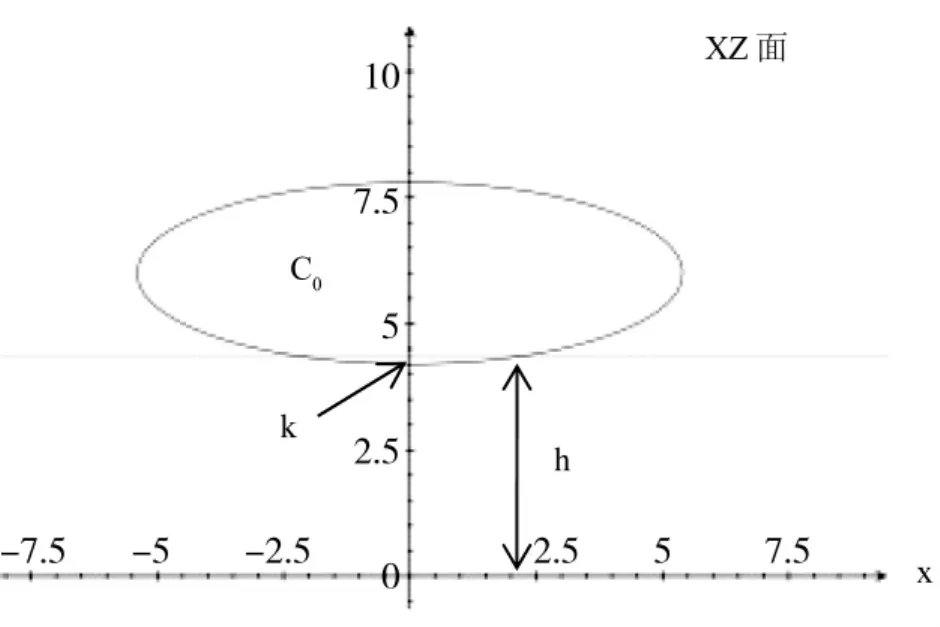
图4 XZ面剖视图

根据基础三维坐标系，建立各几何曲线的方程式。

顺水流方向左侧进口椭圆边墩C1的椭圆方程：

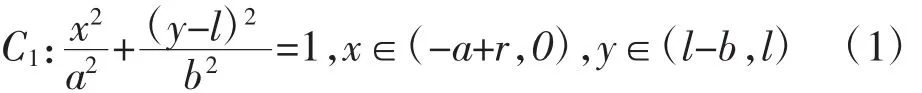
顺水流方向右侧进口椭圆边墩C2的椭圆方程：

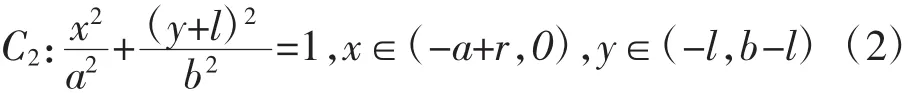
进口顶部椭圆C0方程：

4 依据表达式进行求解

4.1 计算曲线长度

所求曲线为椭圆主体相交线，求其长度时运用求空间曲线长度的方法求解。

4.2 求解原理

空间曲线的求法是对平面曲线求法的拓展，运用微元法，将空间曲线分割为无穷多个直线段，利用直线段与空间直线在XY平面上的投影之间的关系进行求解。

设空间的两个面分别为F（x，y，z）=0 面和G（x，y，z）=0 面，将空间曲线的方程设为，并且暂假定其为一条平滑的曲线，设P1（x1，x1，x1），P2（x2，x2，x2）为曲线上的两个端点，求P1与P2两点间的弧长。

切向量与XY平面的夹角φ的正弦与余弦公式分别为：

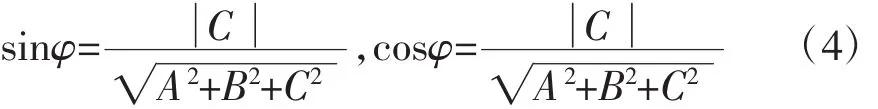
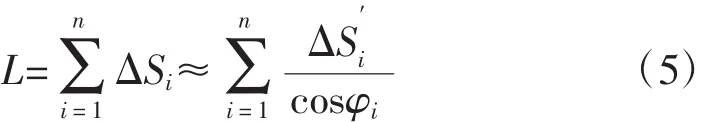
用λ表示若干个小弧段在空间曲线上的长度，用λ′表示在投影曲线上的最大长度，则λ→0时，也有λ′→0，得出：

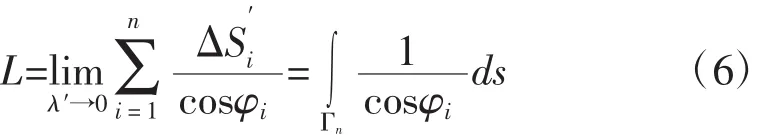
设空间曲线的参数方程为x=x（t），y=y（t），z=z（t），（α≤t≤β），其中t表示将自变量（x，y，z）化为关于t的函数，假定它是光滑曲线。由微分法知，曲线Γ上任一点（x（t），y（t），z（t））的切向量切向量与平面 XY的夹角 φ的余弦cosφ=。空间曲线在XY平面上的投影曲线 ΓXY的方程为x=x（t），y=y（t），z=z（t），（α≤t≤β），在XY平面上的投影曲线ΓXY的弧微分，则可得该段弧长公式：

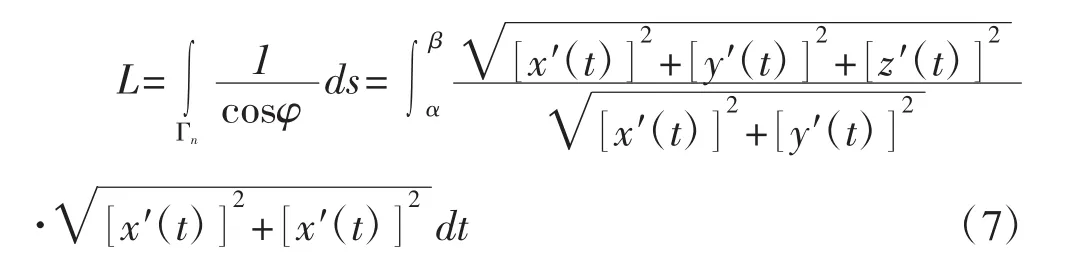
通过公式计算，可以得到两个椭圆两两相交，不同高程时的相关弧长数据。通过计算得到的弧长数据，能够使模板制作的尺寸更加精确，避免了传统模板制作根据邻近部位尺寸进行推断椭圆尺寸的弊端，施工椭圆曲面能够更加优化，特别是多椭圆曲面相交时更加流畅。

5 结语

椭圆大体积混凝土结构施工，给工程的设计、模板制作和施工增加了一定的难度，但是使用椭圆曲面的水工建筑在传递荷载、满足水流动能衔接、抗冲刷能力等方面起到的作用，其他形状是没有可比性的。通过将三个椭圆面放到三维空间中建立的空间方程，能够更加准确地计算出模板设计所需要的空间尺寸，为模板制作和大体积混凝土一次成型施工，提供了极大的便利性。