利用采样安全系数的多类不平衡过采样算法*

董明刚，刘 明，敬 超+

1.桂林理工大学信息科学与工程学院，广西桂林 541004

2.广西嵌入式技术与智能系统重点实验室，广西桂林 541004

1 引言

近年来，多类不平衡问题引起了学术界和工业界的广泛关注，如癌症检测、故障检查等。多类不平衡问题指的是个别类（小类）的样本数量比其他类（大类）要少得多，并且小类更加重要，这对于传统分类算法来说是一个巨大的挑战[1-2]；因为传统分类算法都是针对平衡数据集或以误判代价相等为前提的，因此它往往偏向于大类，这就导致了算法整体分类效果的下降[3]。

多类不平衡学习问题主要有两大类解决方法[1-2]：（1）算法级，例如代价敏感学习算法[3]、集成学习算法[4]；（2）数据级，例如欠采样算法[5]（减少大类样本的数量）、过采样算法[6-14]（增加小类样本的数量）。尽管欠采样和过采样方法对解决多类不平衡问题都具有较好的效果，但欠采样方法在删除样本时可能会损失重要的样本信息，而过采样算法不会遇到这种问题[9]。

2002年，Chawla等提出了合成少数过采样技术[6]（synthetic minority oversampling technique,SMOTE）算法，通过在小类样本点和同类近邻之间合成样本点来生成平衡数据集，取得了较好的效果，但它没有对小类样本点进行区分性选择，从而会出现过度泛化和加重类别边界的重叠等问题。针对上述不足，学者们提出了大量的改进算法。自适应合成过采样[7]（adaptive synthetic sampling，ADASYN）通过学习难度来自适应决定合成样本点的数量，从而避免出现过度泛化问题。Han等提出的边界线合成少数过采样技术[8]（borderline synthetic minority over-sampling technique，BSMOTE）只着重于决策边界的小类样本点，其他小类样本点不合成样本点。严远亭等提出了一种构造性覆盖算法的SMOTE过采样方法[9]，认为被孤立的少数类样本点也很重要，提出了基于覆盖内样本点个数与基于覆盖密度这两种选择关键样本的方法来有效地选取典型的少数类样本点进行过采样，从而有效地防止过度泛化。黄海松等提出了一种基于样本特性的新型过采样方式[10]，它综合考虑了数据集中不同类别的类内距离、类间距离与不平衡度之间的关系，对数据集进行距离带划分，可以很好地区分开不同类别，从而有效地防止了类别重叠问题。很多研究也将选择权重与过采样算法相结合，Barua等在2014年提出了大类加权小类过采样技术[11]（majority weighted minority oversampling technique,MWMOTE），该算法根据学习难度来计算权重，并且只在同一个聚类簇的范围内生成新的样本点，可以有效地避免边界重叠问题。Zhu等提出的多类不平衡过采样[12]（synthetic minority oversampling for multiclass，SMOM）技术则是考虑到了过度泛化问题，首先利用聚类方法对样本点进行划分，再计算每个邻域方向的权重，从而避免了过度泛化。

综上所述，尽管在多类不平衡学习上已经取得了大量的优异成果，但过度泛化问题和多类不平衡问题中更严重的类别重叠问题仍然没有得到很好的解决，总体的分类性能还是稍显不足，因此本文提出了一种利用采样安全系数的多类不平衡过采样（sampling safety coefficient for multi-class imbalance oversampling，SSCMIO）算法。首先利用样本点的局部特性，本文提出了近邻采样安全系数，为那些会产生过度泛化的邻域方向分配较小的选择权重，选择那些较为安全的邻域方向合成样本点，从而避免过度泛化。考虑到多类不平衡问题更加严重的类别重叠问题，本文提出了反向近邻采样安全系数，为那些异常的样本点分配一个较小的选择权重，从而避免合成样本点侵入到其他类别区域，减轻多类不平衡数据集中更为严重的类别重叠问题。最后将SSCMIO算法与7种典型的过采样算法对来自KEEL[15]和UCI[16]机器学习数据库上的16个数据集进行了预处理，使用基于C4.5决策树的RIPPER[17]分类器进行分类，结果表明经过SSCMIO算法预处理过的数据集有更好的分类效果。

2 基于选择权重的过采样算法

2.1 MWMOTE算法

MWMOTE[11]算法主要是考虑到某些小类样本点难以学习和类别边界重叠问题，首先它重新定义了边界点，将边界点作为难以学习的小类样本点，再与聚类方法结合。算法的主要描述如下：

（1）首先找出大类的边界点，再根据大类边界点定义出小类的边界点，这些小类的边界点就是难以学习的小类样本点。

（2）根据密度因子和靠近因子每个样本点计算选择权重，详细信息参见文献[11]。

（3）根据选择权重在同一个聚类簇的范围内合成新的样本点。

2.2 自适应半监督加权过采样算法

Nekooeimehr等在2016年提出了自适应半监督加权过采样[13]（adaptive semi-unsupervised weighted oversampling，A-SUWO）算法。首先，为了防止过度重叠，该算法使用半监督聚类算法对小类样本点进行聚类，为同一簇内的样本点计算选择权重，并且在聚类过程中对小类样本的簇边界进行严格限制，从而避免重叠样本的产生。同时对原始的数据集先进行一次分类，根据分类错误率和混淆矩阵来自适应确定每个样本点所需要的合成样本点数量。在合成样本点的时候，只有在同一簇内的小类样本点才能合成样本点，减少合成样本点侵入到其他类区域，降低了生成重叠样本的机会。

2.3 SMOM算法

SMOM[12]算法是Zhu等在2017年提出来的，与SMOTE算法的随机合成新的样本点不同，SMOM将选择权重分配给每个邻域方向，对于可以产生过度泛化的邻域方向赋予较小的选择权重，从而避免过度泛化。算法主要描述如下：

（1）使用聚类算法将小类样本点划分为优秀样本点和被困样本点。

（2）对于每个被困样本点，根据过度泛化因子和复杂因子来计算其选择权重，对于那些优秀样本点则赋予一个定值权重，详细信息参见文献[12]。

（3）若样本点为被困样本点，则根据选择权重来选择近邻，运用式（1）来合成样本点，否则随机选择近邻，运用式（1）来合成样本点。

其中，Xnew表示新合成的样本点，X和Xneighbor分别表示某一样本点和它的任意一个近邻，rand为随机函数，可以产生一个[0,1]之间的随机数。

3 利用采样安全系数的多类不平衡过采样算法

如今多类不平衡问题已经引起了广泛的关注，但现有的过采样算法有可能会导致过度泛化问题，使得算法整体的分类性能下降[12]。并且多类不平衡问题相较于两类不平衡问题拥有更加复杂的类别边界，从而导致了不同类别之间会出现更加严重的类别重叠现象，增加了分类难度。针对以上两个问题，本文提出了利用采样安全系数的多类不平衡过采样算法。首先为了防止过度泛化，提出了近邻采样安全系数，为那些过度泛化的邻域分配一个较小的选择权重，然后运用反向近邻采样安全系数来防止合成样本点侵入到其他类别区域，从而降低了类的识别难度，提升了算法的整体性能。

3.1 近邻采样安全系数

现有的过采样方法在处理多类不平衡这一更具挑战性的问题时，往往会导致过度泛化。考虑到数据集中的每个样本点的近邻对分类结果的贡献都不同，这意味着一些近邻更重要，对分类结果影响更大，故本文提出了近邻采样安全系数，它考虑了样本点的局部特性，为那些会产生过度泛化的邻域方向分配较小的选择权重，选择那些较为安全的邻域方向合成样本点，从而避免过度泛化，提升算法的整体性能。

如图1所示，以二维数据为例，图中有3类数据，圆形样本点表示当前需要过采样的小类，其他为大类。小类中任意样本点Xi的k1个近邻分布在虚线圆内，虚线圆被相互垂直的两条实线分成了A、B、C、D四部分。将Xi点的右上区域按图中的垂直虚线分为3个区域A1、A2、A3。由于SMOTE方法是在样本点Xi和其近邻Yj之间随机合成样本点，由图可知，在区域A2和A3内存在其他类别样本点对合成样本点的影响远比区域A1要小得多，故选定区域A1作为邻域。在区域D中样本点Xn，邻域内其他类别的样本点相对而言较少，分配较高的选择权重，并且为其他邻域方向分配一个较小的权重，可以很好地避免过度泛化问题，提高了算法的总体分类性能。

Fig.1 Neighbor sampling safety coefficient图1 近邻采样安全系数

近邻安全系数很好地反映了样本点的局部特性，用来衡量样本点Xi和其近邻Yj之间的泛化程度，对于那些会产生严重过度泛化的邻域方向分配较小的选择权重，从而提升合成样本点的质量，降低类的识别难度。它可以表示为：

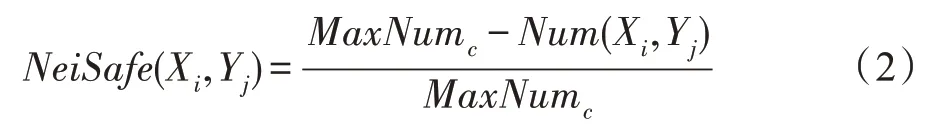
其中，MaxNumc表示Xc内其他类别样本点的最大数量，Num(Xi,Yj)表示Xj i邻域内其他类别样本点的数量，NeiSafe(Xi,Yj)表示样本点Xi和其第j个近邻Yj之间的采样安全系数。

近邻采样安全系数的伪代码如算法1所示。

算法1近邻采样安全系数

3.2 反向近邻采样安全系数

相较于两类不平衡问题，多类不平衡问题中不同类别之间重叠现象更加严重，类别边界更加模糊。考虑到不同类别之间的重叠问题，防止合成样本点侵入到其他类别区域，故采用了反向近邻采样安全系数，从而避免合成侵入到其他类别区域的样本点。它的定义如下：

其中，max、mean分别表示最大值函数和平均值函数；RN表示同一类别所有样本的反向近邻数量的集合；NeiSafe表示样本点的反向近邻与该样本点的近邻安全系数的集合。

反向近邻安全系数很好地反映了样本点的全局特性，若样本点的反向近邻安全系数很小，那么该样本点很可能是潜在的异常样本点，并且侵入了其他类别区域，因此为此类样本点分配一个较小的权重，可以很好地减轻多类不平衡中更严重的类别重叠问题，提高了类的识别度。如图2所示，给出了小类样本点X1、X2、X3和X4的近邻虚线圆，由图可知样本点X1的反向近邻有X2、X3和X4，其反向近邻采样安全系数很小，故该样本点是异常的样本点，存在于重叠的边界区域，若对其合成大量样本就会加重类别重叠问题，使得分类性能大大降低，故采用反向近邻采样安全系数为此类样本点分配一个较小的选择权重，减轻类别重叠问题。

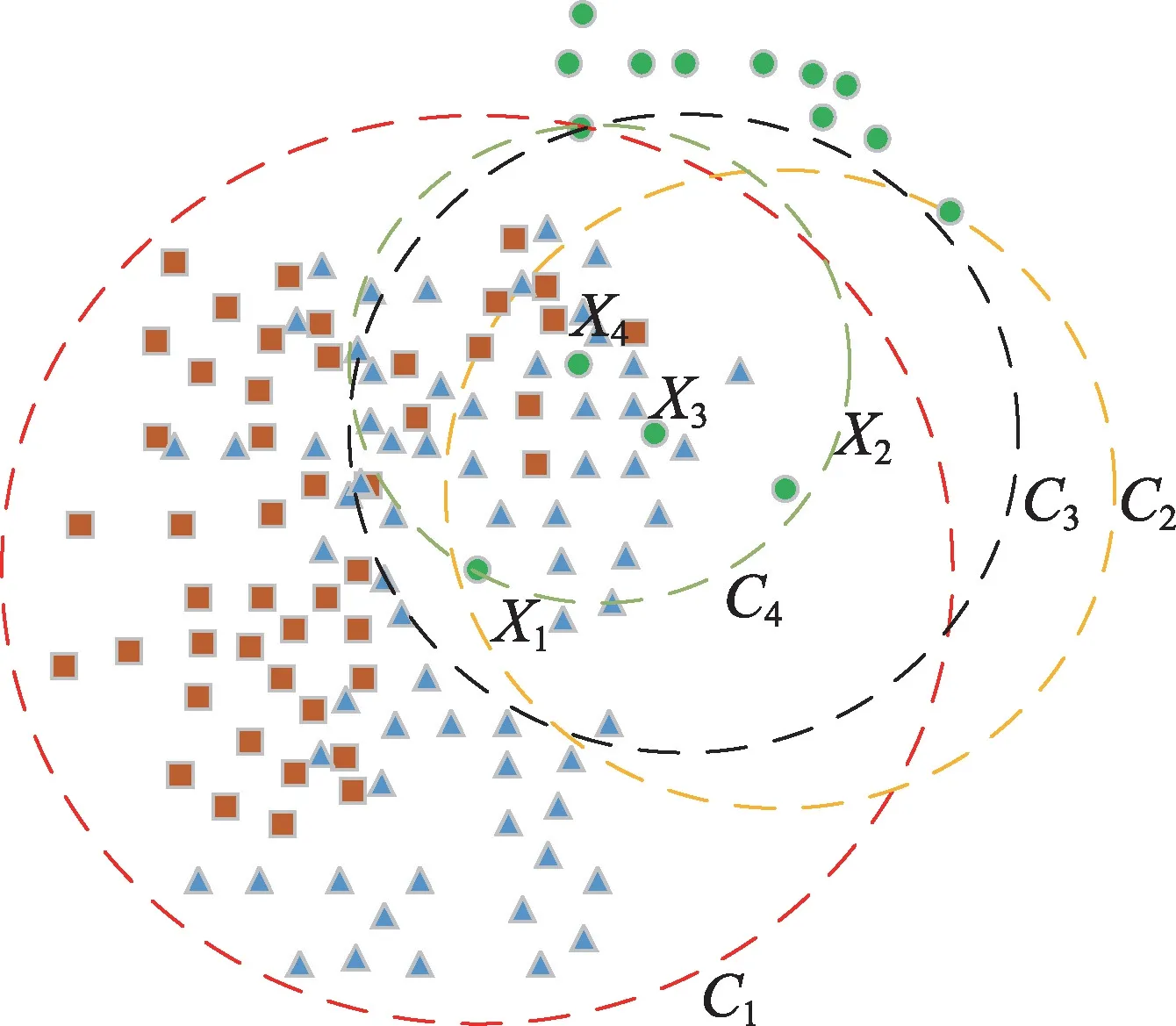
Fig.2 Reverse neighbor sampling safety coefficient图2 反向近邻采样安全系数

反向近邻采样安全系数的伪代码如算法2所示。

算法2反向近邻采样安全系数

3.3 SSCMIO算法主框架

采样安全系数决定应该选择哪些样本点来合成样本点。更高的安全系数意味着其合成样本点不会导致过度泛化，也能避免侵入到其他类别区域，减轻类别重叠，提升了合成样本点的质量，因此将这些合成样本添加到数据集中可以获得更高的分类精度。采样安全系数的定义如下：

SSCMIO算法主框架伪代码如算法3所示。首先为了防止过度泛化，利用样本点的局部特性，采用近邻采样安全系数为小类样本点的每个邻域分配选择权重，并且若该近邻采样安全系数为0，则不在该邻域内合成样本点；考虑到不同类别之间的重叠问题，利用样本点的全局特性，计算出样本点的反向近邻采样安全系数，从而避免合成的样本点侵入到其他类别区域，利用式（4）为每个样本点分配采样安全系数。

算法3SSCMIO算法主框架

3.4 时间复杂度分析

假定数据集中的第c个小类数量为Nc，设所有的小类点的数量为n，即n=，计算一个样本点的近邻采样安全系数和反向近邻采样安全系数的时间复杂度均为O(logn+k1)，其中k1为计算安全系数时的近邻和反向近邻数量，O(logn)为计算一个样本点的k1个近邻的时间复杂度，且k1远小于n，故SSCMIO算法时间复杂度为O(nlogn)。

4 仿真实验

4.1 实验设置与数据集

本文是在Windows 8系统下实现的，使用了WEKA平台[18]中基于C4.5决策树的RIPPER分类器[17]进行分类，分类器参数使用了WEKA平台下算法的默认值，并且采用5折交叉验证，独立运行10次，取平均值作为最终结果。对比算法有SMOTE[6]、ADASYN[7]、BSMOTE[8]，基于分类超平面的混合采样算法（hybrid sampling algorithm based on support vector machine，SVM_HS）[19]、MWMOTE[11]、SMOM[12]、ASUWO[13]，这些算法的参数均采用算法的默认参数，经过实验对比，发现算法中的k1取值为4可以取得最好的性能，具体的实验对比见4.4节。

为了验证算法的有效性，本文采用了来自KEEL[15]和UCI[16]机器学习数据库的16个数据集进行验证，将过采样后得到的平衡数据集用基于C4.5决策树的RIPPER[17]分类器进行分类，文中的数据集在不平衡率（imbalance rate，IR）大于1.45时判定为小类，IR为最大类与最小类的数量比值，数据集的基本信息如表1所示。

Table 1 Basic information of datasets表1 数据集的基本信息

4.2 性能评价指标

采用多类不平衡数据集中常用的Precision[1,20-21]、Recall[1,20-21]、F-measure[22]、MG[23]、MAUC[24]这5个指标来评价算法的优劣性。其定义如式（5）～式（9）所示：

其中，TP表示正类样本预测为正类的数量；FN表示正类样本预测为负类的数量；FP表示负类样本预测为正类的数量；β一般设置为1；A(ci,cj)=表示类i和类j的AUC面积，且A(ci|cj)与A(cj|ci)不相等。

Precision、Recall和F-measure仅计算最小的类，其中MG和MAUC分别是在二类评价指标G-mean[25]和AUC[26-27]（area under ROC curve）的基础上扩展的多类不平衡学习的评价指标，可以很好地评价算法的整体性能[20]。

4.3 实验结果对比与分析

Table 2 Comparison of Precision表2 Precision 的对比

表2到表6给出了SSCMIO算法和其他7种算法在16个数据集上的5种评价指标对比结果，加粗表示当前数据集的最优值。

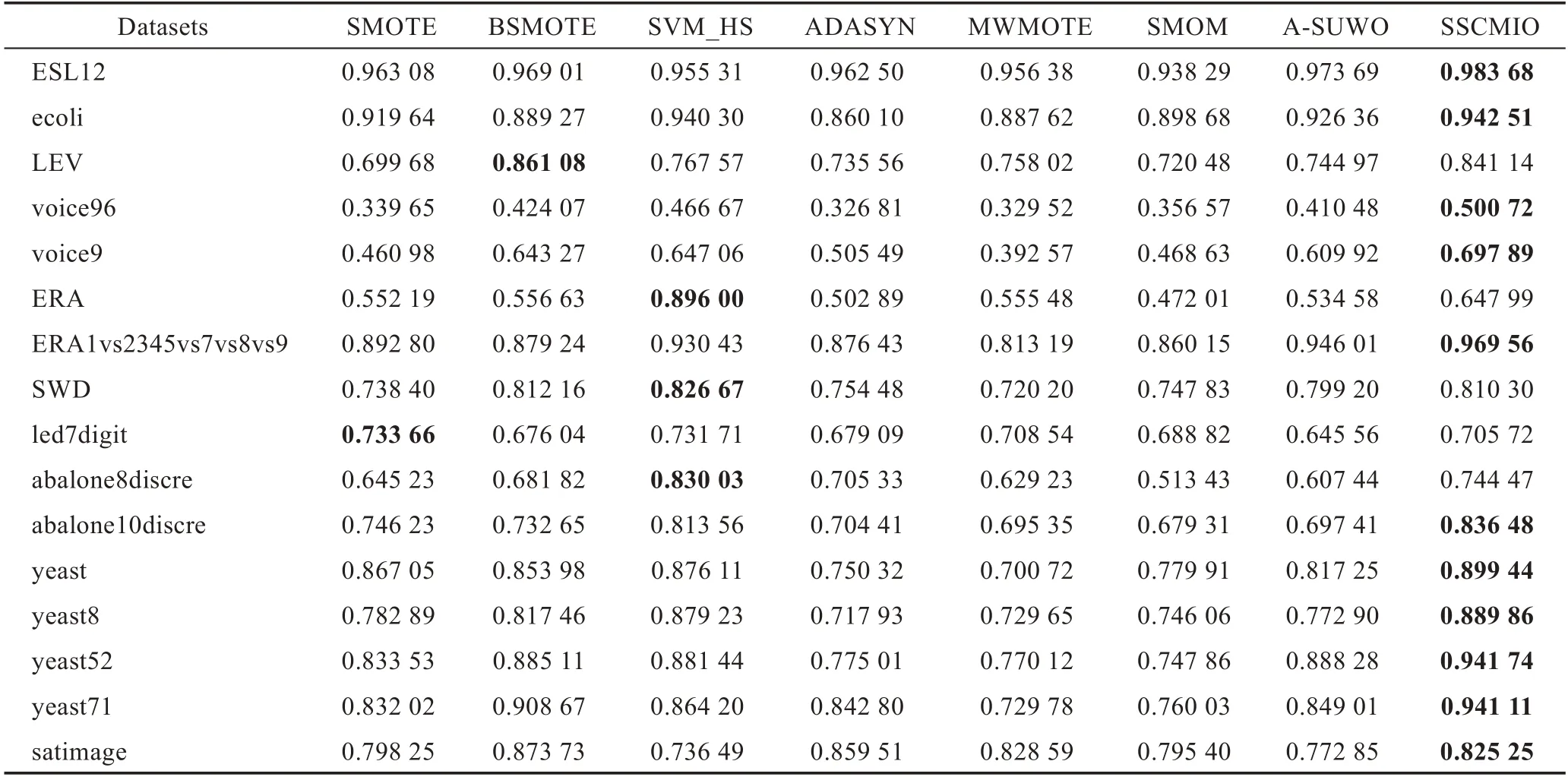
Table 3 Comparison of Recall表3 Recall的对比

Table 4 Comparison of F-measure表4 F-measure的对比

表2展示了8个算法在评价指标Precision上的结果，从表中可以看出在16个数据集中，SSCMIO算法取得了11个最优值，相比于SMOTE、BSMOTE、SVM_HS、ADASYN、MWMOTE、SMOM、A-SUWO平均提升了0.066 5、0.030 4、0.108 6、0.059 8、0.069 2、0.091 2、0.025 5，16个数据集中相比表现最差的算法提升最多的是voice96，提升了0.481 8。

表3展示了8个算法在评价指标Recall上的结果，从表中可以看出在16个数据集中，SSCMIO算法取得了11个最优值，相比于SMOTE、BSMOTE、SVM_HS、ADASYN、MWMOTE、SMOM、A-SUWO平均提升了0.085 8、0.044 6、0.008 4、0.101 2、0.123 3、0.125 3、0.073 9，16个数据集中相比表现最差的算法提升最多的是voice9，提升了0.305 3。

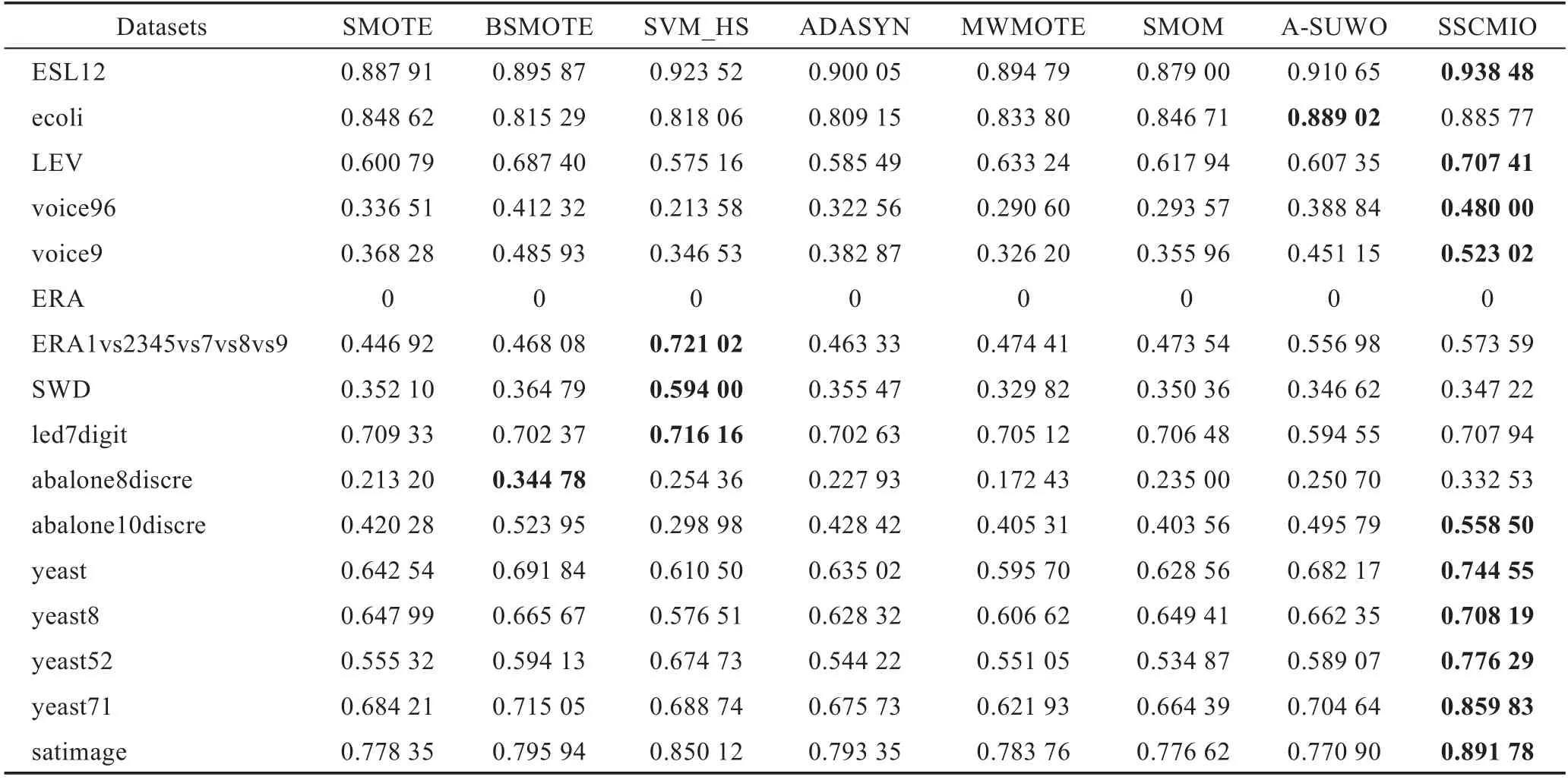
Table 5 Comparison of MG表5 MG 的对比

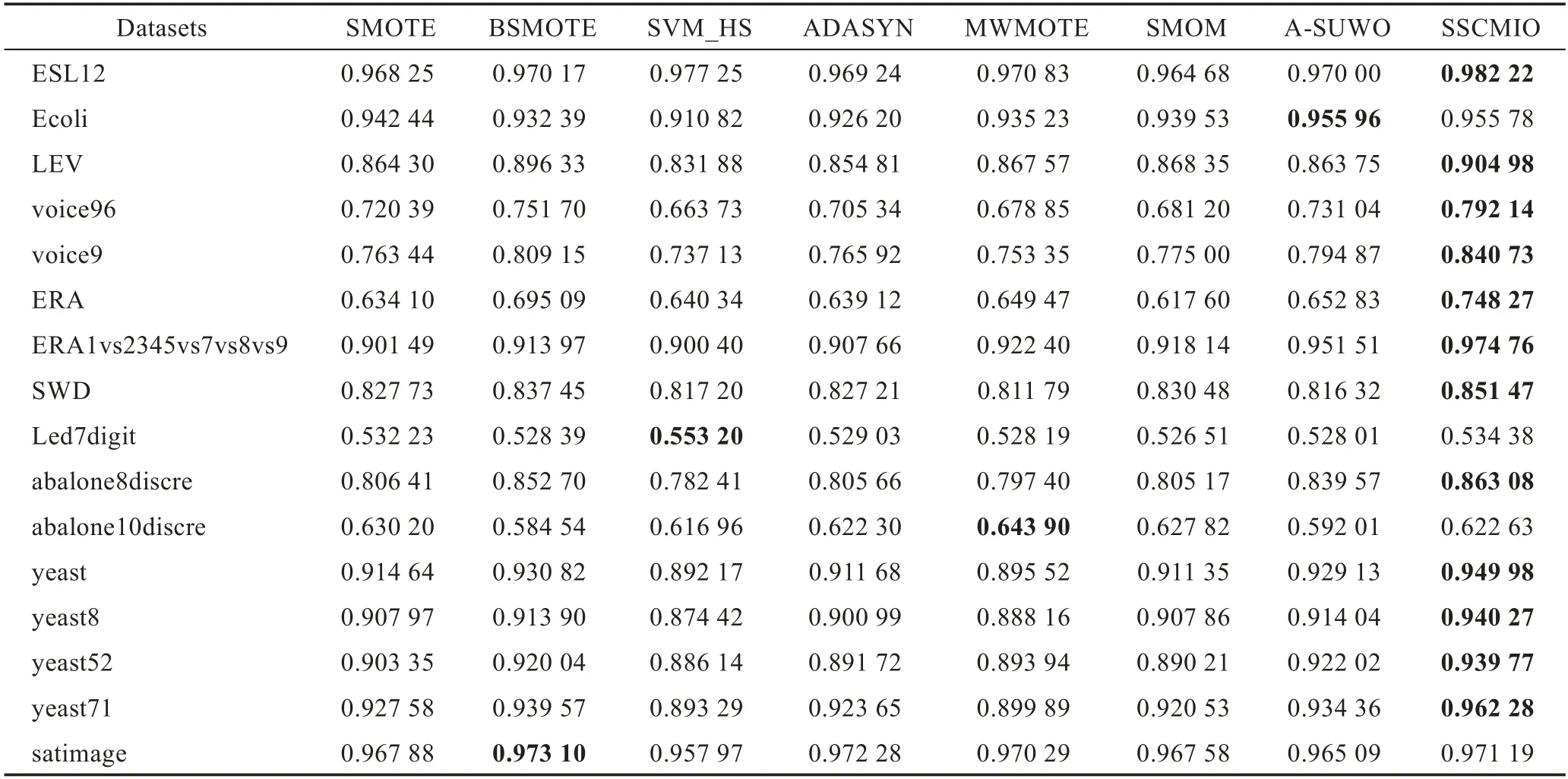
Table 6 Comparison of MAUC表6 MAUC 的对比

表4展示了8个算法在评价指标F-measure上的结果，从表中可以看出在16个数据集中，SSCMIO算法取得了11个最优值，相比于SMOTE、BSMOTE、SVM_HS、ADASYN、MWMOTE、SMOM、A-SUWO平均提升了0.080 9、0.038 8、0.057 0、0.087 4、0.104 6、0.116 0、0.056 0，16个数据集中相比表现最差的算法提升最多的是voice96，提升了0.342 0。

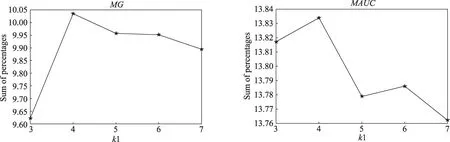
Fig.3 Comparison of k1 value图3 k1值对比

表5展示了8个算法在评价指标MG上的结果，从表中可以看出在16个数据集中，SSCMIO算法取得了11个最优值，其中数据集ERA有个别类别被全部分错，故MG值均为0。相比于SMOTE、BSMOTE、SVM_HS、ADASYN、MWMOTE、SMOM、A-SUWO平均提升了0.096 4、0.054 5、0.073 3、0.098 8、0.113 1、0.101 2、0.070 9，16个数据集中相比表现最差的算法提升最多的是voice96，提升了0.266 4。

表6展示了8个算法在评价指标MAUC上的结果，从表中可以看出在16个数据集中，SSCMIO算法取得了12个最优值，相比于SMOTE、BSMOTE、SVM_HS、ADASYN、MWMOTE、SMOM、A-SUWO平均提升了0.038 8、0.024 0、0.056 2、0.042 6、0.045 4、0.042 6、0.029 6，16个数据集中相比表现最差的算法提升最多的是ERA，提升了0.130 7。

表2到表6的实验结果可以表明SSCMIO算法的有效性，这是因为SSCMIO算法考虑了样本点的局部特性，为样本点的每一个邻域计算选择权重，从而有效避免了过度泛化；再从全局特性出发，采用反向近邻安全系数减少了噪声和离群点的影响，也减轻了类别边界的重叠问题，使得合成的样本点更加合理，降低了分类器的分类难度，从而提升了算法的总体性能。

4.4 参数值的讨论

如图3所示，本文给出了SSCMIO算法在k1取不同值时的折线图，图中纵坐标分别表示在16个数据集上的MG和MAUC这两个指标上的百分比之和，横坐标表示不同的k1值。MG和MAUC均是由二类评价指标拓展而来，能够很好地描述算法的总体性能。从图中可以看出当k1取值为4时，SSCMIO算法的效果是最佳的。相比k1的其他取值，在MG上，16个数据集总的最大提升为0.413 0，在MAUC上的最大提升为0.071 7，故本文将k1的值设置为4。

5 结束语

本文提出了一种利用采样安全系数的多类不平衡过采样算法（SSCMIO）来处理多类不平衡问题。首先为了防止过度泛化，充分利用样本点的局部特性，提出了近邻采样安全系数；然后利用样本点的全局特性，提出了反向近邻采样安全系数，防止合成样本点侵入到其他类别区域，很好地减轻了不同类别之间的重叠问题。将SSCMIO算法与7种典型的过采样算法在16种不同平衡度的真实数据集上进行了对比实验，实验结果表明在大多数的数据集上SSCMIO算法表现得更优。

下一步工作将从以下两方面开展：（1）用于实验的数据集都是数值型的，未来将研究SSCMIO算法应用到非数值型数据集和混合型数据集；（2）可以研究如何将采样安全系数和聚类方法相结合，以便更好地防止过度泛化和重叠问题。