探讨数形结合思想在初中数学解题中的应用
王家升
(福建省泉州市晋江市池店中学 362212)
一、数形结合的思想在初中数学解题中的作用
1.促进学生思维能力的发展
初中的数学知识随着教学的深入,难度在不断加大,让很多学生在解题过程中出现问题,而在初中数学解题中运用数形结合思想有利于促使复杂难懂的数学题简单形象化,有助于学生理解.简单化的过程体现在数量关系与图形能够相互转化和补充上.在学生数学答题时,将数形结合思想融入进去,可以让学生更好地理解题意,降低答题难度,促进学生发散思维,寻找多种解题思路和方法,对课本知识的理解和掌握程度提升有着重要意义.
学生在解题中运用数形结合思想能提高学生的审题能力和答题思维,增强学生观察力和注意力,教师应不断向学生渗透数形结合的思想,促进学生的思维能力发展.
2.培养学生的学习兴趣
初中数学解题过程对于学生来说枯燥,且其中涉及逻辑和思维,难度大,导致学生普遍对数学的学习兴趣低.为了防止此现象的产生,教师在进行数学讲题过程中要充分利用数形结合思想,让数学问题与图形相结合,提高学生的学习兴趣,吸引其注意力,也让学生在数学学习中找到乐趣,同时降低了学习数学难度,使学生乐于接受知识,促进其学习能力的提高.
在数学解题中,通过数形结合的方式使得学生的学习兴趣提高,会促使学生更加积极主动进行数学探讨,激发其学习欲望,提高学生的学习热情,增强数学学习的效率,实现预期教学效果.
二、数形结合思想在初中数学解题中的应用探析
1.利用数轴解决相关问题
利用数轴能够解决不等式问题,在初中数学学习中,不等式是重要的学习内容,要求学生可以解一元一次不等式,在数轴中标出不等式的解集,这是中考必考知识点,也是典型数形结合问题.在解一元一次不等式时要注意两点,第一是未知数前面的系数是负数时,当系数化1后,不等式的不等号要变方向,若是“﹥”,要变为“<”;第二是“≤、≥”表示实心,“>、<”表示空心.
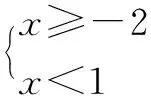
如图1,在求不等式的解集时,为了清楚地得到不等式在数轴上的解集,重点在于x<1是空心,x≥2的方向,因而选择A.

图1
利用数轴也可以解决找中位数和众数问题,中位数是将各个变量按大小的顺序排列后,处于中间的变量值就被称为中位数,而众数是指所有变量中出现次数最多的数值,这是数学中常见的两个概念,很容易理解.中位数问题需要对数据进行排列,而众数问题需要对数值进行统计,利用数轴可以降低数值记忆的难度,使数值更加清楚直观地表现.
例2 (10年第4题)今年6月11日,我省九个地区的最高气温与最低气温如图2所示,则这九个地区该天的最高气温的众数为( ).

图2
A.27℃ B.29℃ C.30℃ D.31℃
如图2所示,可以在数轴中标记数据,数据每出现一次就在相应地方标记1,进行累计,得到最多的就是众数,如图3,得知答案为D.
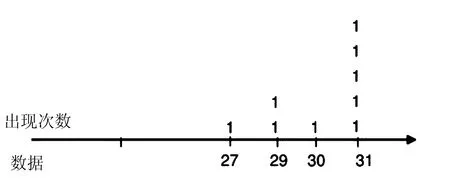
图3
2.利用直角坐标系解决函数问题
在初中数学的学习过程中,函数内容占据着很大的比重,包括常数函数、一次函数、二次函数以及反比例函数等,函数问题在解答的过程中逻辑性强,主要的方法是运行数形结合.在解函数问题时,要画出函数的图象,让复杂的函数简单形象化,要掌握函数关系式中参数的作用,同时教师在教学的过程中要培养学生认识函数关系的类型,每当学生看到题目就能马上判断出是什么类型的函数,就算题中不给图象,也可根据所学知识画出函数图象,解决数学难题.
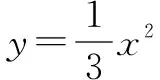
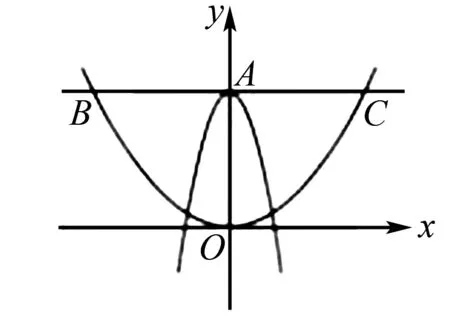
图4
在解一元二次函数问题时,函数图象有四个要点,第一是看开口方向,二是看对称轴,三是看顶点坐标,四是看特殊点,如与x轴的交点或是与y轴的交点,如图4,此题中虽不知a的系数,但与y轴有交点,能够得出A(0,3),从而看出过A与x轴平行的直线是y=3,A、B、C纵坐标相同,可以求出B(-3,3),C(3,3),最后得出BC的长度为6.
3.利用图形解决实际问题
利用图形可以解决概率问题,在计算简单的概率问题时可以画树形图,让题目更加直观化、简单化.
例4 有甲、乙两个不透明的口袋,甲口袋中有3个球,分别标有数字0,2,5;乙口袋中有3个球,分别标有数字0,1,4.这6个球除了所标数字以外没有任何区别,从甲乙中各随机摸出一个球,用树形图的方法,求摸出两个球上数字之和为6的概率.
解此道题时,在看到一大段数字和文字后,学生往往会产生厌烦的心理,而概率问题所蕴含的逻辑思维较强,不借助外力纯在脑海中思考会给学生增加解题的困难,而使用数形结合的方法,根据题意画树形图能够让题意简化,更容易得出答案,如图5,可以得出P(数字之和为6)=2/9.

图5
利用数形结合能够解决三角问题,在利用数形结合解三角问题时,有一个前提是问题最后必须转化到直角三角形中,利用直角三角形的相关知识进行解答.
例5 (12年第20题)如图6,有一个晾衣架放置在水平地面上,在其示意图中,支架OA、OB的长均为108cm,支架OA与水平晾衣杆OC的夹角∠AOC为59°,求支架两个着地点之间的距离AB.(结果精确到0.1cm)(参考数据:sin59°=0.86,cos59°=0.52,tan59°=1.66)如图6,应用数形结合解此题时,很容易能看出图形为等腰三角形,过O点向AB线作高,交点为D,则OD为中线,在直角三角形OAD中,解出AD,则AB等于2倍的AD,具体解法如图7所示.

图6

答:支架两个着地点之间的距离AB约为112.3cm.
因为是应用题,所以最后要写答.
综上所述,可以看出数形结合在初中数学解题中的重要作用,因而教师要注重对数形结合思想的传授,在初中数学教学的过程中要对数与形的关系进行深入探讨和揭示,利用数轴、直角坐标系和图形解决相关问题,帮助学生应对数学难题,为高中数学学习做准备.

