激光照明条件对超振荡平面透镜聚焦性能的影响*
刘康 何韬 刘涛 李国卿 田博 王佳怡 杨树明
(西安交通大学, 机械制造系统工程国家重点实验室, 西安 710049)
超振荡平面透镜(super-oscillatory lens, SOL)是近几年出现的新型平面光学元件, 基于矢量角谱理论设计了振幅型和相位型SOL, 采用时域有限差分法对衍射聚焦光场进行严格电磁仿真计算, 研究发现: 当照明激光束腰半径w0 小于SOL 半径a 时, 超衍射极限聚焦能力明显下降, 聚焦光斑强度衰减超过50%; 束腰半径w0 对相位型SOL 影响更剧烈, 且会发生显著正向焦移; 当w0 不小于2a 时可获得接近理想的聚焦特性. 倾斜照明条件下, 大数值孔径振幅型SOL 一般允许的倾斜角度小于10°, 而相位型SOL 具有宽广的倾角适应性(可超过40°), 聚焦光斑会发生横向展宽, 且强度急剧下降. 大数值孔径SOL 对无限远点物成像会产生显著的负畸变和波动变化的场曲, 小数值孔径SOL 在宽视场范围内则无畸变. 本文研究结果为SOL 在超衍射极限聚焦、超分辨显微成像、飞秒激光直写微纳加工等领域的实际应用提供重要理论支撑.
1 引 言
为了实现远场亚波长聚焦和超分辨成像, 英国南安普顿大学于2012 年首次提出了超振荡透镜(super-oscillatory lens, SOL)[1], 作为一种新的平面光学元件, 其基本原理是利用微纳环带结构实现多光束衍射, 并由相干光场的精细干涉叠加在光学远场区域获得亚波长尺寸的聚焦光斑[1,2]. SOL 是一种微纳同心圆环结构, 与常规的同心圆环光瞳滤波器(或称Toraldo 光瞳滤波器)[3,4], 工作原理截然不同, 前者是利用光的衍射对光场直接聚焦, 后者必须工作于透镜或物镜系统中. SOL 是一种随机优化产生的平面光学元件[1,2,5,6], 与熟知的菲涅耳波带片[7,8]也存在明显区别, 后者是利用波带法直接构造的疏密有致的同心圆环结构. 根据光场调制参数的不同, SOL 可分为振幅型、相位型和复振幅型, 振幅和相位调制分别通过刻蚀金属膜和透明介质材料实现. 由于SOL 具有结构轻薄、易于实现亚波长聚焦和衍射光场定制设计的突出优点, 近几年受到广泛的关注[5,6,9−12]. 主要包括广泛深入的优化设计方法研究[1,5,9−11], 和基于SOL 的超分辨成像应用研究[1,13−15]. 对于引入加工误差后SOL 聚焦性能变化的研究较少, 西安交通大学分析了金属膜的材料和厚度以及照明激光波长对SOL 聚焦特性的影响[16,17]; 西北工业大学初步研究了SOL 环带宽度误差和环带侧壁倾斜度对聚焦性能的影响[18];东南大学基于激光直写技术利用视场拼接的办法加工了大口径SOL 并分析了拼接误差对聚焦性能的影响[19].
目前为止, 激光照明条件对SOL 聚焦性能的影响尚未见相关研究报道, 尚不清楚SOL 实际应用中照明光源振幅分布、倾斜、安装偏差等客观条件下SOL 聚焦性能如何变化, 这些情形都偏离了SOL 优化设计的基本假设条件[1,2,9,10], 目前研究也尚未揭示SOL 对无限远物点成像的像差分布.本文结合矢量角谱(vectorial angular spectrum,VAS)理论和遗传算法(genetic algorithm, GA),在激光均匀照明、垂直入射条件下优化设计典型SOL, 重点基于时域有限差分法(finite-difference time-domain, FDTD)对衍射光场进行严格电磁仿真计算, 通过大量的FDTD 定量计算研究揭示实际应用中激光照明条件对SOL 聚焦特性的影响规律, 并研究揭示离轴倾斜照明(或无限远点物成像)条件下的畸变和场曲像差分布特性, 研究结果将为SOL 在当前超分辨聚焦、显微成像、微纳光刻等领域的广泛工程应用奠定坚实的理论基础.
2 SOL 设计
当矢量偏振光束垂直照射SOL 表面时, 其衍射聚焦过程如图1 所示. 根据VAS 理论, 如果已知SOL 后表面处的横向电场分布, 则SOL 之后空间中任意一点的电场分布均可由VAS 积分表达式计算得到[20], 而SOL 后表面的电场分布近似等于入射场与SOL 衍射孔径标量透过率函数的乘积[1,2,5,6,9]. 根据VAS 理论对任意典型偏振态激光光束的衍射传播过程进行积分描述, 再设定需求目标对衍射光场进行单目标或多目标约束, 建立数学优化模型, 进而通过优化算法(如GA 算法[2]或粒子群优化算法[1])反复迭代计算, 可以优化设计出性能满足(或接近)设计需求的SOL 结构[1,2,5,6,9].

图1 SOL 衍射聚焦示意图Fig. 1. Schematic diagram of diffraction focusing of SOL.
针对最典型的线偏振光(偏振方向设为沿X方向), 基于VAS 理论导出的积分公式[2,9], 利用GA 算法和快速汉克尔变换算法[9,16], 分别优化设计出三组振幅型和相位型的SOL 结构, 参数见表1. 其中, 照明激光波长l= 632.8 nm, 光源垂直入射, 振幅设为均匀分布. SOL 工作介质为空气,SOL 的最大外径为D, 设计焦距为fsol, 环带最小径向宽为∆r,NA是SOL 的数值孔径(NA=sinα,α是最大会聚半角). SOL 的几何结构用每个环带的外环半径值ri表示(i= 1, 2, ···,N,N是最大环带数), 每个环带的透过率用ti表示, 其中振幅型SOL 的透过率“1”和“0”分别表示该环带是透光和不透光, 而相位型SOL 的相位调制量为y= 0,π/2 或π, 对应ti= exp(jy)等于“1”, “j”和“-1”(j 是虚数单位). 第3 节将基于典型SOL 结构(SOL1—6)采用严格电磁仿真方法——FDTD 进行计算分析.
3 激光照明条件对SOL 的影响
3.1 激光振幅分布的影响
针对振幅型SOL1和相位型SOL2(见表1),分别采用束腰半径w0= 2a,a, 2a/3,a/2 的高斯光束进行照明, 其中a为SOL 的半径(a=D/2),高斯光束振幅分布(设在SOL 衍射孔径平面内)表示为

其中A0是光束中心处的幅度. 利用FDTD 三维严格电磁仿真, 振幅型SOL1采用100 nm 厚的铝膜作为光的遮挡介质[1,16,21], 相位型SOL2的相位调制介质采用Si3N4材料, 在l= 632.8 nm 波长下Si3N4的折射率为1.91[22], 通过对Si3N4层的刻蚀产生深度为348 nm 的沟槽进行相位π 的调制.FDTD 采用完全匹配层(perfectly matched layer,PML)作为吸收边界, 设置总场散射场(total-field scattered-field, TFSF)光源边界, FDTD 仿真区域网格划分为20 nm × 20 nm × 20 nm (x,y,z),更精细的网格划分可提高计算精度, 但同时对计算机存储空间的需求迅速增大.
振幅型SOL1仿真计算得到的衍射场沿轴光强分布和焦平面内垂直于偏振方向的光强分布如图2 所示, 其中束腰半径w0=∞对应均匀平面波. 从图3(a)可见, 光源束腰半径w0由∞减小至a/2时, 聚焦光斑的横向半高全宽(full width at half maximum, FWHM)逐渐展宽. 当高斯光的束腰半径w0大于SOL 的半径a时, 聚焦光斑的FWHM仅展宽了1.4%, 光斑强度衰减为等幅度均匀平面波时的43.3%; 而当束腰半径w0小于SOL 衍射孔半径a时, 聚焦光斑由287 nm (0.42l/NA,w0=a)迅速展宽为341 nm (0.50l/NA,w0=a/2), 光斑尺寸增大了19%, SOL 的超衍射极限聚焦的能力逐渐下降(标量衍射理论框架下, 艾里斑的FWHM为0.51l/NA), 同时聚焦光斑的光场强度急剧下降, 仅为原来的18%, 如图3(b)所示.

表1 优化设计的SOL 结构参数Table 1. Structural parameters of optimized SOL.

图2 SOL1 的聚焦光场FDTD 计算结果 (a) 轴向光强分布; (b) 焦平面内横向光强分布(Y 方向)Fig. 2. Focused light field of SOL1 by FDTD simulation:(a) On-axis intensity distribution; (b) transverse intensity distribution in the focal plane (Y-direction).
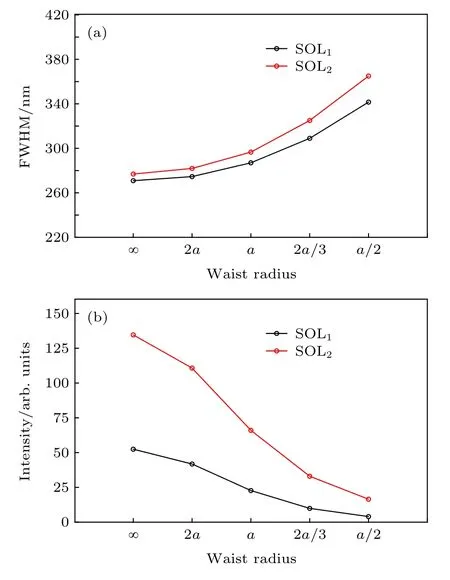
图3 SOL聚焦性能变化(FDTD) (a) 光斑横向尺寸;(b) 光斑中心强度Fig. 3. Focusing performance of SOL (FDTD): (a) Transverse size; (b) central intensity.
类似于振幅型SOL1, 相位型SOL2的聚焦光斑同样随着照明高斯光束的束腰半径的减小而逐渐展宽, 光斑强度迅速减弱, 如图3 和图4 所示.相位型SOL2的光强分布变化更为剧烈, 照明光束的振幅分布对其影响更大, 特别是当束腰半径w0由a减小到a/2 时, 轴向光斑的旁瓣显著增强,并且伴随着显著的轴向正向焦移(160 nm), 横向光斑的FWHM 由297 nm 展宽为365 nm, 尺寸增大了23%, 光斑强度也减弱为原来的25%. 而当高斯光束的束腰半径w0=a时, 横向光斑的FWHM 仅展宽了7.2%, 光斑强度衰减为均匀照明时的49%.
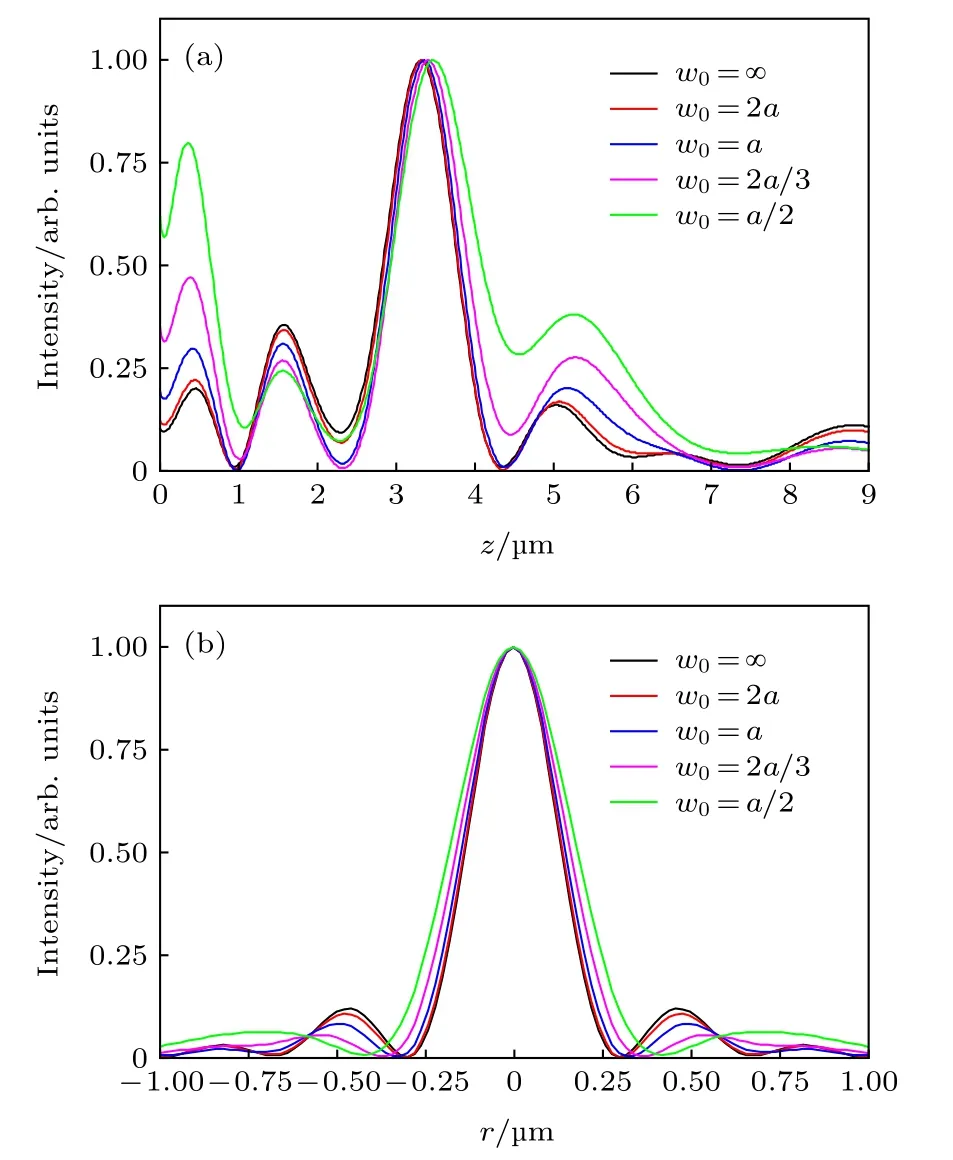
图4 SOL2 的聚焦光场FDTD 计算结果 (a) 轴向光强分布; (b) 焦平面内横向光强分布(Y 方向)Fig. 4. Focused light field of SOL2 by FDTD simulation:(a) On-axis intensity distribution; (b) transverse intensity distribution in the focal plane (Y-direction).
从SOL1和SOL2的FDTD 仿真计算结果不难发现, 对于均匀照明条件下优化设计的SOL, 若采用高斯光束进行照明使用(实际情形), 无论是振幅型还是相位型SOL, 聚焦光斑的分布总体仍然保持了一致的单焦点特性, 但激光的束腰半径会对SOL 聚焦性能产生显著影响, 强度和光斑尺寸在w0≥D(即w0≥2a)时接近理想设计情形. 当束腰半径w0减小至SOL 半径a时, 聚焦光斑尺寸明显展宽, 而光斑强度衰减超过50%, SOL 聚焦光斑的分布影响相对较小. 当束腰半径w0小于SOL 半径a后, 不仅聚焦光斑尺寸会发生显著扩展, 超衍射极限聚焦能力明显下降, 特别对于相位型SOL还会出现显著的正向焦移现象, 光斑的轴向旁瓣也会明显退化.
当前大多数微纳光学研究使用的SOL 半径在几十至百微米量级[1,5,9−11], 由于实际激光光束的束腰半径都在亚毫米至毫米(准直扩束后可增大至数毫米至厘米量级), 远大于SOL 的半径, 因此实际照明情形可按均匀平面波对待. 但为了与常规的光学元件配合使用以及提高SOL 的光能利用率, 需要设计毫米级甚至厘米级的大口径SOL[18,19], 此时SOL 的衍射半径已经等于或大于照明激光束腰半径, 激光光源的振幅分布特性对SOL 聚焦光斑的影响变得尤为显著. 因此, 如果光源束腰半径与SOL 半径相近或更小时, 必须将高斯光束振幅分布代入优化设计过程, 对SOL 进行更加精准的优化设计.
进一步地对X方向线偏振光照明的SOL 聚焦光斑矢量特性进行研究, 以SOL1为例, 在均匀平面波和w0=a/2 高斯光照明条件下焦平面各电场分布如图5 所示. 可以看到平面波入射条件下聚焦光斑中电场Ez和Ey分量在电场总场中的比重较大, 导致聚焦光斑呈扁椭圆形; 而高斯光照明条件下SOL 聚焦光斑的Ez和Ey分量却相对较小, 对合成光斑的分布影响减弱, 光斑最终呈轻微椭圆状. 通过分析不难发现, 由于采用高斯光束进行SOL照明时, 对聚焦光斑Ez和Ey分量贡献最大的外环结构接收到的激光照明强度大大降低, 因此聚焦光斑中的电场Ez和Ey分量减小而Ex成为最主要的分量, 合成光斑将在Ex分布基础上沿着照明光偏振方向轻微展宽.
除了最常见的高斯平面波, 进一步对空心高斯光束[23]和贝塞尔-高斯(Bessel-Gaussian, BG)光束[9]等不同振幅分布照明光源条件下的SOL 聚焦特性进行了分析.
首先基于VAS 理论对X方向线偏振空心高斯光束照明条件下的SOL 聚焦光场分布进行了计算, 发现随着光束空心半径的增大焦平面光斑的Ez和Ey分量占比急剧上升, 呈明显的“哑铃”形分布; 而光场轴向分布则逐渐展宽呈不均匀的“光针”状, 这样的变化与对SOL 进行中心遮挡空间滤波情形类似[24].
其次采用典型的BG 振幅分布的径向偏振态光束, 针对SOL1和SOL2进行矢量衍射计算, 振幅服从[9]

图5 SOL1 聚焦光斑电场分布的FDTD 结果 (a) 均匀平面波照明; (b) w0 = a/2 的高斯光束照明Fig. 5. Electric field distribution of SOL1 by FDTD simulation: (a) Uniform plane beam illumination; (b) w0 = a/2 Gaussian beam illumination.

图6 BG 径向偏振光束照明条件下SOL 聚焦光场的VAS 计算结果 (a), (b) SOL1; (c), (d) SOL2Fig. 6. Focused light intensity of SOL by VAS calculation under BG radially polarized illumination: (a), (b) SOL1; (c), (d) SOL2.

其中J1为第一类一阶贝塞尔函数. 设高斯束腰半径等于SOL1半径(w0= 8 µm), 基于VAS 理论进行聚焦光场计算, 结果如图6 所示. 可见, 采用径向偏振BG 光束照明的SOL, 聚焦光斑横向尺寸与X 线偏振均匀平面光照明条件下的Y向光斑尺寸大小接近且略微偏大, 而光斑轴向分布严重变形, 根本原因是这里使用的SOL 是采用线偏振光设计的, 如果改为径向偏振光照明则其聚焦性能不能达到最优, 此时应该在径向偏振光照明条件下重新优化设计[9].
3.2 激光倾斜照明的影响
SOL 对有一定倾斜角度(倾角)的单色相干平行光束直接聚焦(等价于对轴外无穷远物点进行衍射聚焦成像), 或者可将SOL 用作管镜进行无限远物点的光学成像, 如图7 所示. 此外, 由于装调误差等原因也可能导致入射光束方向与SOL 元件表面的法线方向存在一定的夹角, 如图8 所示. 这些都偏离了目前SOL 的设计基本条件要求, 即均假设单色激光垂直照明, 此时SOL 是否依旧能有效聚焦, 或者对倾斜平行光有一定的视场角范围, 以及聚焦光斑分布会如何变化, 将直接影响SOL 的实际应用.

图7 SOL 对倾斜平行光的衍射聚焦成像示意图Fig. 7. Schematic diagram of diffraction focused imaging by SOL under oblique illumination.
首先对振幅型SOL 在倾斜入射下的聚焦性能进行了初步研究, 发现振幅型SOL 对入射光束倾角(偏转角度)十分敏感. 图9 为振幅型SOL 的倾斜照明FDTD 聚焦计算结果, 其中大数值孔径SOL5(NA= 0.93)的聚焦光斑在倾斜角度ω=12◦时出现了明显的弥散现象, 而在ω=15◦时失去聚焦能力; 小数值孔径SOL6(NA= 0.44)在ω=18◦倾斜照明条件下光斑出现显著变形, 在ω=21◦时光斑严重退化, 此时SOL 失去对该倾角平行光束的良好聚焦. 总体而言, 振幅型SOL 聚焦性能严重依赖于照明光束倾角大小, 一般仅允许相对较小角度(ω⩽10◦)的倾斜照明, 小数值孔径SOL 具有相对较弱的倾角依赖性.
图8 倾斜平行光照明的SOL 衍射聚焦示意图Fig. 8. Schematic diagram of diffraction focusing by SOL under oblique illumination.
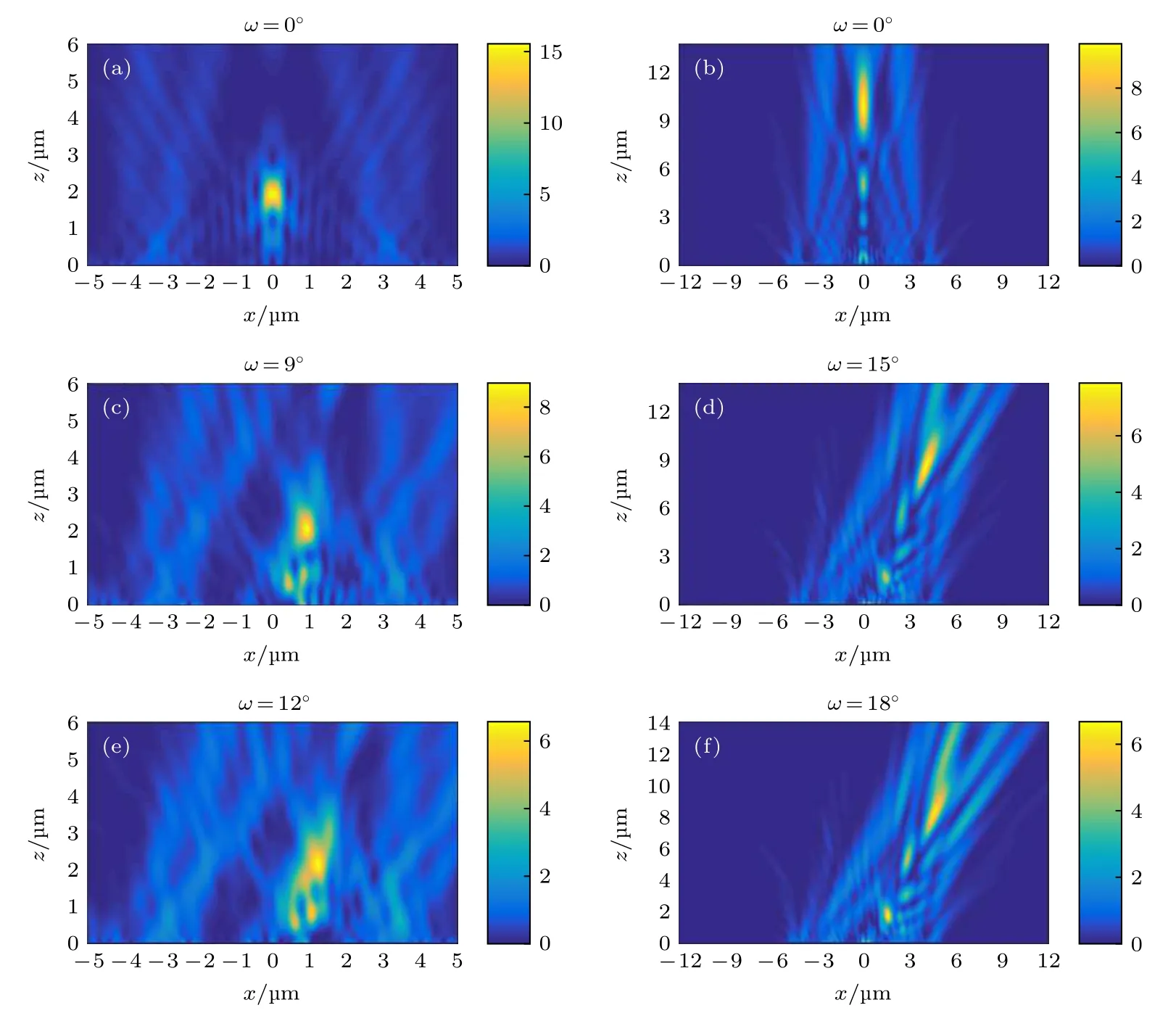
图9 振幅型SOL 的倾斜照明FDTD 聚焦计算结果 (a), (c), (e) SOL5; (b), (d), (f) SOL6Fig. 9. Focusing results of amplitude-type SOL under oblique illumination: (a), (c), (e) SOL5; (b), (d), (f) SOL6.

图10 倾斜照明SOL 的聚焦光斑尺寸 (a) FWHM x ; (b) FWHM zFig. 10. Focal spot size of SOL under oblique illumination: (a) FWHM x ; (b) FWHM z .
相比之下, 相位型SOL 则可以在较大角度的倾斜照明条件下进行光束聚焦, FDTD 仿真计算结果显示, 在倾斜角度最大达到ω=42◦时相位型SOL3和SOL4仍然能够实现良好聚焦, 远大于振幅型SOL 允许的入射倾角大小. 除了对入射光倾斜角度具有更高的适应性, 相位型SOL 的聚焦效率以及对入射光场调制的灵活性等也远优于振幅型SOL, 有望在未来获得更广泛的使用, 因此, 下面针对相位型SOL 进行详细比较分析, 包含大数值孔径和小数值孔径SOL 两类.
对于NA= 0.93 的相位型SOL3和NA= 0.45的相位型SOL4, 将平行光束进行间隔为3°的等间距倾斜(ω=0◦—42◦), 对聚焦光场分别进行FDTD严格电磁仿真计算. FDTD仿真模型中SOL 的相位调制层采用SiO2材料, 在632.8 nm波长下折射率为1.457, 通过对SiO2层的刻蚀, 产生深度为346 nm 的沟槽进行相位π/2 的调制. 仿真采用PML 边界条件、TFSF 光源, 仿真区域网格划分为20 nm × 20 nm × 20 nm (x,y,z).
首先以聚焦光斑中强度最高的点作为焦点中心, 定量统计聚焦光斑的横向和轴向尺寸(FWHMx和FWHMz), 如图10 所示. 随着入射激光倾斜角度的逐步增加, SOL3聚焦光斑的横向和轴向尺寸波动较大, 光斑的横向尺寸大致呈增大趋势, 轴向尺寸则呈现先增大后减小的变化趋势, 其中光斑横向FWHM 最大展宽了52%, 而光斑轴向尺寸波动更为明显, 最大展宽达到了94%. 对于小数值孔径的SOL4, 光斑的横向和轴向FWHM 变化则呈现出一定的规律: 当倾斜角度处于18°以内时, 光斑的FWHMx保持着较高的稳定性, 倾斜角度达到18°时聚焦光斑也仅有47 nm 的展宽, 光斑的FWHMz则随着倾斜角度的增加逐步减小且整体呈现一定的线性关系; 当倾斜角度超过18°后,光斑的横、轴向尺寸均开始出现明显波动, 并且在42°的倾斜角度下光斑的横向尺寸出现急剧变化,SOL 的聚焦能力退化严重.
其次, 聚焦光斑强度也随着倾斜角度的增大而出现显著下降, 如图11 所示. 对于大数值孔径的SOL3, 倾斜角度在0°—9°的变化过程中, 光斑强度急剧衰减了61%, 而在倾斜角度达到18°以后光斑的强度衰减逐渐趋于平缓, 总体处于较低水平. 对于小数值孔径的SOL4, 与前述光斑尺寸一样, 光斑强度在18°以内的倾斜入射角度下能够保持较高稳定性, 最高仅衰减了11%, 而在18°以后光斑强度变化开始变得较为明显, 到42°的倾斜角度时强度衰减已经达到了69%.

图11 不同照明角度下SOL 的聚焦光斑强度Fig. 11. Focal intensity of SOL varying with oblique illumination angle.
3.3 无限远物点成像的畸变和场曲
对聚焦光斑的位置进行了定量统计分析, 发现在倾斜角度ω小于18°范围内SOL3的聚焦光斑倾斜角度位置ω′与入射激光倾斜角度ω存在较好的线性关系, 如图12(a)所示, 经最小二乘拟合后该线性斜率为2.03, 拟合均方根误差为1.077. 进一步对SOL3的出射、入射角度的正切之比进行计算, 发现该比值随着倾斜角度的增加而逐渐减小, 如图12(b)所示, 而Γ表示图7 所示成像系统的垂轴放大率的调制系数, 该调制系数随入射角度变化则意味着SOL3不同的垂轴位置具有不同的放大倍数β, 可利用下式表示:

因此像面会产生畸变. 对于SOL3, 当倾斜角 度ω小 于18°时,利用正切倍角公式,得到Γ ≈2/(1−tan2ω), 即可以通过入射角估算出垂轴放大倍数β. 对于小数值孔径的SOL4, 聚焦光斑的角度位置ω′与入射角ω之间的线性关系更为明显,倾斜角度ω在0°—27°的角度范围内, 最小二乘拟合的线性斜率为1.15, 拟合均方根误差为0.142(对应微小畸变), 比值Γ保持良好的一致性, 显示出远比SOL3好的规律性, 根据(2)式, 此时具有类似透镜成像系统, 垂轴放大倍数为常数(无畸变).
利用(2)式, 结合折射透镜光学系统中相对畸变的定义[25], 以小角度(本文可取3°)对应的实际垂轴放大倍率为基准, 则相对畸变

显然由图12(b)可知,q′ <0 (负畸变), 对应桶形畸变.
由聚焦光斑在横向和轴向位置的变化可以得到SOL 聚焦产生的场曲和畸变(针对无限远物体成像), 轴向和横向位置分别用Xf和Zf表示, 类似于单色几何像差折射透镜系统的分析, 以激光垂直入射时焦点所在的平面为基准面, SOL3和SOL4在XZ平面(子午平面)的场曲曲线如图13 所示,随着入射激光倾斜角度的增大, 场曲逐渐增大, 在倾斜角度分别达到18°和27°过后, 两者的场曲开始出现明显波动, 场曲的存在意味着聚焦像点(或离轴焦点)的轴向位置会发生明显的移动.

图12 聚焦光斑角位置变化 (a) ω - ω′ 关系曲线; (b) ω - Γ 关系曲线Fig. 12. Angle position of focusing spot: (a) ω - ω′ ; (b) ω - Γ .

图13 SOL 的场曲 (a) SOL3; (b) SOL4Fig. 13. Field curvature of SOL: (a) SOL3; (b) SOL4.
根据上述两种数值孔径SOL 的仿真结果和分析, 可以发现虽然在0°—42°的倾斜角度范围内两者均能保持聚焦功能, 但聚焦性能完全不同; 大数值孔径的SOL3对照明光的倾斜角度比较敏感, 即便在较小的倾斜角度, 聚焦光斑的横、纵向尺寸、光强等都会出现明显的波动和降低, 小数值孔径的SOL4则在一定的倾斜角度内表现出了良好的稳定性, 在18°的范围内不论是光斑的横纵向尺寸、强度、角度位置还是场曲和畸变等像差都表现出了良好的稳定性.
4 结 论
本文基于VAS 理论设计了多组典型的SOL,重点采用FDTD 严格电磁仿真计算分析激光照明条件(振幅分布、倾斜角度等)对SOL 聚焦的影响. 仿真和分析结果表明, 在照明高斯光束的束腰半径大于SOL 半径(w0≥D)时, 振幅型和相位型SOL 的聚焦性能均接近理想情形, 而当束腰半径小于SOL 半径(w0

