“平面与平面垂直的判定”教学设计与评析

郑娟 李芳娥

【摘 要】《数学课程标准》指出：高中数学课程以学生发展为本，落实立德树人根本任务，培育科学精神和创新意识，提升数学学科核心素养。本节课主要通过两个设计突破教学难点，突出教学重点。一是用“问题串”的设计探究二面角的平面角的做法的合理性;二是通过动手操作探究发现面面垂直的判定定理。

【关键词】二面角;平面角;面面垂直;直观想象;逻辑推理;数学抽象

一、教学内容及其解析

本课时选自人教A版《普通高中课程标准试验教科书·数学2（必修）》（以下统称“教材”）第二章第三节的第二课时，是空间垂直关系的重点和难点内容，也是高考的考查热点，是“类比”“转化”思想的又一重要体现。

二、教学目标及其解析

1.理解二面角和二面角的平面角的定义;掌握平面与平面垂直的判定定理;能应用判定定理证明一些简单的面面垂直问题。

2.感知面面垂直的现象，类比探究平面角的做法，讨论并抽象判定定理;体会空间关系和平面关系的类比与转化，提高空间想象能力、数学建模能力和抽象概括能力。

3.感受数学文化的魅力，激发学生学习数学的兴趣，提高数学学科核心素养;感受中国诗词文化的魅力，渗透爱国主义教育。

三、学生学情分析

高中生思维活跃，参与意识、语言表达能力、自主探究能力较强，故采用启发、探究和实验结合的教学方法。

四、教学策略分析

教学方法：启发式教学法、讨论教学法、直观演示法、讲练结合法等。

教学媒体：投影仪、多媒体视频、PPT课件、几何画板软件、学案等。

五、教学过程设计

（一）创设情境，明确探究方向

朗诵诗人名作《茅屋为秋风所破歌》，感受诗人忧国忧民的家国情怀，实现课堂德育目标。通过多媒体展示“茅屋”与“大厦”两个实物，引导学生复习平面与平面的位置关系，从而引入本节课题。

学生活动：通过聆听诗朗诵，感受诗人的家国情怀，回顾平面与平面的位置关系。

教师活动：用诗朗诵对学生进行爱国主义教育，引导学生回顾平面与平面的位置关系。

设计意图：精选的诗作，既对学生渗透了爱国主义教育，同时达到复习回顾的效果。

（二）因势利导，认识二面角

1.二面角的相关概念和表示

借助多媒体课件展现实例图片，实物图形抽象成数学图形并进行展示;多媒体课件动态演示平面内的角和二面角的形成过程;引导学生通过类比得出二面角的定义及其相关概念，教师补充二面角的画法及其表示方法。

学生活动：归纳二面角的要素，观看视频，概括二面角的定义。

教师活动：启发学生从经典实例中抽象出几何元素，加强学生对二面角的直观感知，鼓励学生类比已有知识，概括定义，并适时给出二面角的图形表示和符号表示。

设计意图：通过课件动态演示，降低了学生在概念抽象上的难度。通过类比迁移，使得概念的生成更加合理、自然。

2.二面角的平面角及其作法

怎样做出一个平面内的角来度量二面角的大小呢？对于这一问题采用如下“问题串”的方式进行探究。

问题1：我们常说“把门开大一些，把窗户关小一些”，看来二面角是有大小的，我们该如何刻画二面角的大小呢？

问题2：我们有过度量空间角的经历吗？

设计意图：通过回顾已有知识，学生自然就会联想到用“平面化”的思想，即用“平面角”来度量“二面角”。

问题3：我们可以借助这样的经验，寻找一个能随着二面角变化而变化的平面内的角，那么这个平面内的角的顶点，以及角的两边应该选在什么位置合适呢？

问题4：当我们选择某种方法度量一个量时，必须考虑到“唯一性”，在各种位置关系中，哪一种位置关系具有唯一性呢？

问题5：那你能完整描述一下这个角的特点吗？

教师适时补充，完成二面角的平面角的定义。

问题6：这样的平面角唯一吗？

至此，二面角的平面角的探究全部完成。

问题7：数学源于生活，我们教室内就有很多的二面角，你能举出一些例子吗？

学生举例，教师将重点放在学生所举的直二面角的例子，类比得出面面垂直定义及表示。

学生活动：分析问题，分享成果。

教师活动：以“问题串”的形式，引导学生探究二面角的平面的作法，采用类比的方法得出面面垂直的定义。

设计意图：通过“问题串”的设计，問题层层深入，思维逐步提升，使学生理解到数学定义、概念的形成并非凭空想象，而是科学的、合理的。

（三）承上启下，开启定理发现之旅

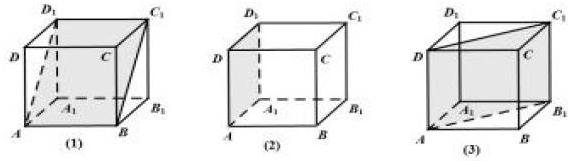
例1：正方体ABCD-A1B1C1D1中，找出下列二面角的一个平面角。

（1）二面角D1-AB-D;（2）二面角A1-AD-C;（3）二面角A1-AC-B。

学生活动：读题、思考、回答，找出二面角的平面角。

教师活动：出示问题，提问学生，及时做出鼓励性评价。

设计意图：通过本题，学生能感受到定义法证明面面垂直的可操作性差，激发学生对探究判定定理的思考和期待。此时，教师顺水推舟，就可以将课堂学习再向前推进一步，教学过程自然流畅。

（四）水到渠成，发现判定定理

1.探究面面垂直的判定定理

探究活动：在文明城市创建活动中，我市打算在文化广场立一块公益广告牌，你能用所学知，帮助工人检测所立的广告牌与地面是否垂直吗？

学生活动：分组讨论，提出方案，小组汇报，总结判定定理所需要的条件。

教师活动：巡视各组活动情况，引导学生通过“选择工具—说明做法—解释原理—总结结论”几个环节展开讨论，汇总学生成果并形成判定定理。

设计意图：这一活动的目的是培养学生用数学眼光观察世界、用数学思维思考世界、用数学语言表达世界。通过活动培养学生的空间想象能力、抽象概括能力、逻辑推理能力等核心素养。同时，精选的公益广告牌也在无形中实现了立德树人的德育目标。

2.例题拓展，巩固强化定理应用

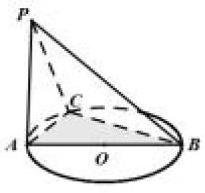
例2：如图，AB是 O的直径，PA垂直于 O所在的平面，C是圆周上不同于A，B的任意一点。

（1）求证：平面PAC⊥平面ABC。

（2）求证：平面PAC⊥平面PBC。

学生活动：思考，回答。

教师活动：个别提问，范例书写，规范步骤。

设计意图：通过本题的范例书写，规范步骤，达到本节课对“直观想象”、“逻辑推理”等核心素养的培养。同时，例题的拓展，又实现了数学史及数学文化的渗透，激发了学生学习的兴趣。

（五）学以致用，促进知能提升

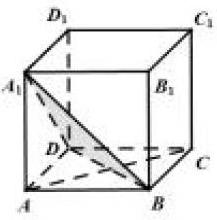
练习：在正方体中ABCD-A1B1C1D1，求证：平面ACC1A1⊥平面A1BD。

学生活动：学生独立完成。

教师活动：投影展示学生作答情况，点评。

设计意图：通过课堂练习，深化了三种垂直关系相互转化的认识，培养学生逻辑推理能力核心素养。

（六）鱼渔之得，综述收获体会

学生活动：回忆，总结，作答。

教师活动：启发，总结，点评，补充。

设计意图：协助学生在完成本节学习后，将其收获纳入到已有的知识网络，帮助学生构建空间位置关系的知识体系，实现知识和能力的全面提高。

六、课堂教学目标检测

基础题：完成教材第73页习题2。3的A第3题、第4题。

提高题：结合学习过的空间平行关系的判定定理、性质定理、空间垂直的判定定理，类比发现其他判定面面垂直的命题，给出你的结论。

设计意图：分层作业的设计符合因材施教的理念，实现不同的人在数学上有不同的发展这一目标。

专家点评：本节课是在已有空间平行关系、直线与平面垂直的判定及性質以及斜线与平面所成的角的认知基础上，对空间平面与平面位置关系的又一次探索。

作课人引领学生通过实例，抽象出平面与平面的位置关系，引入自然，符合学生的认知特点;在学生已有角的度量经历的基础上，利用“问题串”的生成二面角的平面角概念，突破学生对概念及空间问;通过直观感知、操作确认，生成平面与平面垂直的判定定理。由具体到抽象，本节课的设计很好地实现了数学学科素养中对学生直观想象及数学抽象能力的培养。同时精选的公益广告牌也实现了课堂的德育功能，是一节符合现代教学理念的优质课。