基于MATLAB/Simulink的汽车主动悬架控制器的设计与仿真

李滨

摘 要：本文在建立1/4车辆模型的基础上，根据牛顿运动定律建立动力学方程，并根据现代控制理论的知识建立状态方程，采用最优控制策略，分别对被动悬架和主动悬架进行模拟和仿真。车辆悬架的特性可以从车身垂直加速度、悬架动行程及轮胎动位移进行研究。并对两种悬架的仿真结果进行了详细的比较分析和说明。

关键词：MATLAB;主动悬架;设计与仿真;汽车

0 引言

汽车悬架分被动悬架、半主动悬架和主动悬架，本文主要分析主动悬架的最优控制，并对主动悬架和被动悬架仿真结果进行分析和比较。车辆悬架的评价指标是车身加速度、悬架动行程和轮胎动位移。基于MATLAB/Simulink软件进行仿真。

1 建立1/4悬架模型

1/4悬架模型如下图：

2 LQG控制器设计

LQG控制器设计的性能指标J其表达式为：

（6）

式中，分别为轮胎动位移、悬架动行程和车身垂向振动加速度的加权系数。

将性能指标J的表达式（8）改写成矩阵形式：

（7）

式中，Q对应于状态变量的权重矩阵;R为约束输入信号大小的权重矩阵;N为耦合项。

当车辆参数值和加权系数值确定后，最优控制反馈增益矩阵可由黎卡提（Riccati）方程求出，其形式如下：

（8）

最優控制反馈增益矩阵，由车辆参数和加权系数决定。根据任意时刻的反馈变量，就可得出t时刻作动器的最优控制力，即：

3 仿真输出与分析

选择某轿车的后悬架作为相关计算参数：，，，悬架工作空间，，u=20m/s，，，，，主动悬架，，被动悬架，。白噪声的生成可直接调用MATLAB函数WGN（M，N，P），取M=10001，N=1，P=20。设定采用时间为0.005s、车速为20m/s时，仿真路面长度1km，仿真时间为50s。

根据所建立的系统状态方程式（4）及最优性能指标函数（7），利用已知的矩阵A、B、Q、R、N，调用MATLAB中的线性二次最优控制设计函数，即可完成最优主动悬架控制器的设计。

输出的结果中，K为最优控制反馈增益矩阵，S为黎卡提方程的解，E为系统闭环特征根。带入仿真输入参数，可求得最优反馈增益矩阵K为：

K=（711.88 -1241.5 -19284 -2038.5 20864）

黎卡提方程的解为：

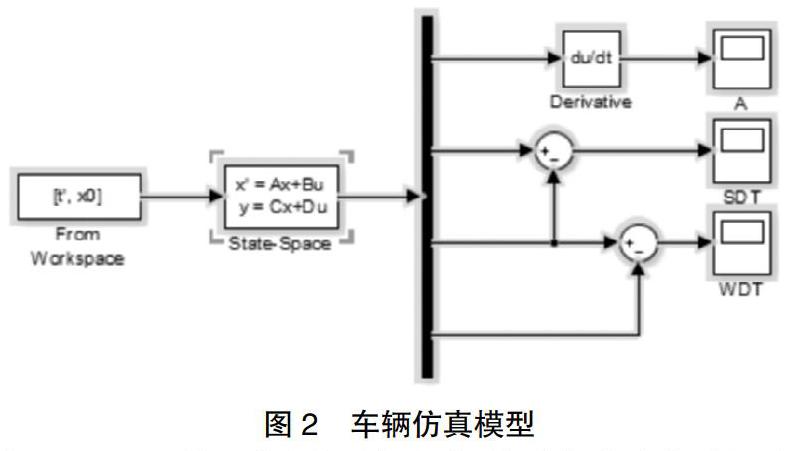
在Simulink环境下建立的最优主动悬架车辆仿真模型框图如图2所示。LQR主动悬架系统和被动悬架系统的时域仿真结果分别如图3、图4所示，包括路面位移输入、悬架动行程SDT（t）、轮胎动位移WDT（t）及车身加速度BA（t）。

图3、图4、图5为被动悬架仿真图。

4 结论

图中对主动悬架的仿真需要进一步探讨。只对被动悬架的车身加速度、悬架动行程、轮胎动位移进行仿真。关于主动悬架与被动悬架的优越性，据有关资料可知，主动悬架提高了平顺性、舒适性和操纵稳定性，应用前景广阔。

参考文献：

[1]兰波，喻凡，刘娇蛟.主动悬架LQG控制器设计[J].系统仿真学报，2003（15）：138-140.

[2]余志生.汽车理论[M].北京：机械工业出版社，1999.