基于反向随机投影的神经网络改进算法

许邓艳，卢民荣

(1.福建工程学院 应用技术学院，福建 福州 350118；2.福建江夏学院 会计学院，福建 福州 350108；3.福建省社科研究基地财务与会计研究中心，福建 福州 350108)

近年来，神经网络的算法、模型及研究内容相当广泛，反映出多学科交叉技术领域的特点。以人工智能的应用为代表，如专家系统、机器人等应用系统，已经具备机器学习的特性[1-2]。基于神经网络算法的深度学习，能够让机器自我学习以及模式识别，相关学习算法不仅受学者关注，也吸引了IBM、Google、Baidu等IT公司投入大量应用研发。随着机器学习、深度学习的发展，学习网络规模越来越大、复杂度越来越高，学习效率问题成为算法最关键的也是最难的研究热点[3-4]。从1986年提出BP神经网络(back propagation, BP)至今，BP仍是目前研究和应用最广泛的模型[5]，受网络的中间层数、各层的神经元个数的影响，全连接神经网络规模通常都比较大，因此网络的学习速度慢和容易陷入局部极小值[6-7]。以卷积神经网络(convolutional neural networks, CNN)为典型代表的局部连接网络，通过池化、卷积可以大幅降低网络的规模，有效提升训练效率，然而卷积感受野过大就会影响感知效率，另外随着网络深度的增加，不断加深抽象层级也会影响计算效率[8]。循环神经网络(recurrent neural network, RNN，也称递归神经网络)和在RNN基础上延伸出来的长短期记忆人工神经网络(long-short term memory, LSTM)，主要是通过全连接网络中的数据集局部随机训练，在效率和准确率上比BP有明显优势。另一些学者是通过适当的低秩因子来移除深度神经网络卷积核中的冗余参数来降低网络规模，也有基于参数共享和 Huffman 编码来压缩网络的规模，从而实现比较高的压缩率[9-11]。近年，运用深度神经网络连接权重稀疏和对滤波器进行谱聚类后修剪等大幅提升了网络的效率[7,12]。综上，CNN网络通过数据特征卷积(再卷积)的局部网络逐层缩小后，效率大幅提升，而RNN和LSTM则是训练数据的局部化(随机性)缩小训练规模，以及基于这些模型提出的快速学习由于不具有图灵完备性而导致学习能力也低于全连接网络，考虑了效率则损失了准确率。因此，我们有必要从“局部连接”回到“全连接”的神经网络进行连接优化[13]，从而在保证准确率的情况下提升效率。

针对神经网络的效率问题，本研究提出一种基于反向随机局部投影的神经网络效率改进算法，引入连接缩小参数降低除倒数第2层至输出层外的其它网络规模，同时运用缩减集合解决传统基于随机取数存在一定信息丢失的概率问题，倒数第2层至输出层仍然保留“全连接”，从而实现从“局部连接”回到“全连接”神经网络的连接优化。最后通过26字母发音数据集ISOLET不同参数、不同网络层数的测试，来论证在保证不降低准确率的情况下，基于反向随机局部投影的网络在语音识别上的效率有较大提升。

1 模型

1.1 BP全连接网络原理

以典型的3层神经网络为例，网络实现主要分为前向网络和反向网络，神经网络的节点与权重的工作原理基本雷同，具体步骤如下[5-7]：

第一步：各层节点准备，设置网络的迭代次数。

第二步：初始化各层全连接权重，第一次需要初始化，后面根据误差反向传播进行更新。

第1至2层：0到1之间随机生成n×h权重矩阵，用W1表示；同理生成第2至3层权重h×m，用W2表示。

第三步：第1层到第2层前向信息传输。

首先，把第1层的输入转为第1层的输出即O1=X，再与W1计算获得第2层的输入(公式1)，然后对第2层的输入进行激活，生成第2层的输出(公式2)。

(1)

式中，O1i表示第1层的第i个节点(神经元)的输出，X′j表示第2层的第j个节点的输入。

O2=σ(X′j)

(2)

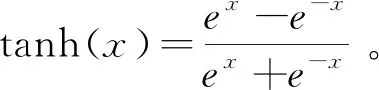
第四步：重复第二至第三步(对于多层神经网络，重复至输出层即结束前向网络)，将矩阵计算换成W2，输出激活后为O3，然后判断网络的输出O3和实际输出的Y的误差。

第五步：计算总误差，并进行反向传播。

首先把网络的输出O3和实际输出的Y进行相差比较，获得总误差E，计算如公式3示。

(3)

然后进行反向传播第3层(也叫输出层、最终层、结果层等，示例为3层网络)到第2层，由于矩阵运算的原因，需要对第2至3层权重h×m，W2进行转置即W2T=W(m×h)，进行计算误差平摊即每个节点的误差ΔE，如公式4示。

(4)

式中，ΔE2表示第2层节点输出的平均误差，∂为学习率，不同应用则网络设定的权值不一样，因为设置过高会使梯度下降时找不到最优解，设置过低又容易让网络效率变低。

第六步：更新权重，这也是网络的核心。

根据上述公式(3)、(4)推导，把平均误差计算出来分摊至各个连接的权重进行调节，如公式5。

ΔW2=∂×E3×σ(O3)×(1-σ(O3))·O3T

(5)

式中，ΔW2更新后的第2层权重，∂为学习率，σ表示激活函数，O3T表示O3的转置。

第七步：重复第五至第六步(对于多层神经网络，重复至输入层即结束反向网络)，计算误码差和权重矩阵的更新，即完成W1的更新。

第八步：继续前向网络、反向网络即第二到第七步，直至整个网络迭代结束。

1.2 局部网络模型

权重是神经网络的核心部分[13]，其计算量也是最大的部分，前向网络中需要同神经元进行矩阵相乘运算，在反向网络中需要转置后与误差进行矩阵相乘运算，再根据学习率修正权重矩阵的值，因此，我们可以在现行网络结构和工作原理不变的情况下，用降低权重矩阵思路优化局部连接，提升网络的效率(本方法也称为局部网络模型)，另一方面，为了让输出层与输入层有较为直接的连接则让第2至3层网络连接(最后一层的网络连接)仍然使用全连接方式，具体改进后的网络示意图如图1。

图1 改进连接后的神经网络结构

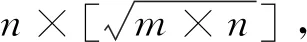
1.3 算法实现

基于改进的权重连接主要是通过输出端(相对上一层网络的输入，图1中的右侧数字节点)反向局部投影到输入端(相对下一层网络的输出，图1中的右侧非数字节点)，为方便表达，仍然使用上述经典的3层网络，变量的定义同上述说明，具体平均分布投影过程如下：

第一步：根据缩小参数计算连接数公式(6)和输入端节点平均输出公式(7)。

(6)

(7)

式中，[]表示取整，如果有小数直接去除，Omin表示输入端节点平均最少输出。而Omin+1则为平均最多输出Omax。

第二步：反向随机局部投影连接，反向投影具体做法：

(1)从输出端第一节点开始，从输入端节点1至n(输入端集合用I表示)中随机取局部连接数Oceil，被取出的节点设置该节点随机权重W(Oceil×h)并记入输入端节点号；

(2)对已经反向投影的局部连接节点进行记数Oc(从1开始)，为保证所有输入节点信息都能被传递到输出端，在输入端集合I中随机去除Oc中记数最高的至缩减集合R中。

(3)改进随机局部连接算法，部分研究表明随机局部连接算法确实有效，但传统基于概率的随机取数存在一定信息丢失的概率问题[13,16-17]。改进方法为如果I的数量小于Oceil，则从R中再还原至少I的数量和Oceil数量差，还原规则为Oc最小优先，如已经达到输入端节点最多输出(Oavg+1)则不再被还原，具体I、R、Oceil等集合的出入栈结构如图2示。

(4)继续输出端下一节点的投影，重复(1)-(3)，直至输出端节点结束。

第三步：如果为多层网络，重复第一、二步，直到倒数第2层。

第四步：从“局部连接”再到全连接。

在倒数第2层到最后1层，采用全连接输出，不要再使用局部投影，以免前期输入到最终输出产生丢失。

在3层网络中，第2至3层仍为全连接网络，因此算法主要以网络中第2层(输出端)到第1层(输入端)反向随机局部投影连接算法进行设计，具体实现的过程如下：

Inputs: input_nodes: 输入端,hidden_nodes:输出端,reduce: 连接缩小参数.Outputs: weights: 局部投影的权重.n, h←len(input_nodes),len(hidden_nodes) #输入与输出端节点数oceil,omin,omax←ceil(n/reduce) , int(oceil *h/n), omin +1#节点连接数 oc,weights←[(0*2) for i in range(h)] #实始化节点取数和权重矩阵I,T,R←[(i*1) for i in range(h)],[],[]#初始化输入端、临时和缩减集合for i in range(hidden_nodes):#输出端节点迭代I←I-R#排除缩减集合for j in range(oceil): #随机取数,个数为oceil则停止t←random.randint(I)T.add(t),I.pop(t)#临时入栈和出栈oc[t]←oc[t]+1#计数累加weights.append([t,random(0,1)])#随机权重oc←sort(oc,1)#按计数排序R←random(I,oc, random.randint(I)) #随机去除if(len(I)< oceil ):#防止去除过多I←oc[i]<= omaxΔ random(R,oc, random.randint(R)):pass#超限则不再被还原 return weights

2 实验及分析

实验硬件为联想Thinkserver RD350服务器，操作系统为Windows Server 2008 R2。在软件配置上需要Python3.7及相应的运行包安装，开发环境使用MyEclipse 2017 CI开发工具。在实验中，采用BP网络和本算法针对同一标准数据集进行比较。

2.1 参数设置及数据集

为了方便实验对比，采用标准的数据集ISOLET(训练集和测试集各26组数据，表2)进行不同侧面的准确率、效率对比分析，以论证反向随机局部投影的改进情况。基于BP神经网络的局部连接网络参数(主要设置了缩减参数)配置如表1示。

表1 局部连接网络模型的参数配置

表2 ISOLET数据集

2.2 模型参数变化策略

反向随机局部投影的神经网络规模随着缩减参数的增加而增少，其模型效率提升，但准确率也会下降，反之也成立，当缩减参数为1.0时则模型和全连接网络一致。基于神经网络的深度学习模型中，随着迭代次数增加(也称“学习深入”)，网络训练结果准确率逐步提高，但时间消耗也增加(也称“学习效率”)[18]，实验以准确率能达到90%左右效果为基准，取迭代20次，分别调整缩减参数为：1.4、1.6、1.8、2.0、2.5、3.0进行实验，准确率、效率实验效果如图3、图4所示。

在图3中，由于全连接网络是没有缩减参数调节，因此其准确率是一条固定的直线，在实验的数据集中缩减参数在1.8、2.0时基本和全网络接近，而设置为1.4、1.6时则优于传统全连接网络。不过缩减参数设置较大，如取3.0时其准确率下降较多，因此，ISOLET数据集不宜设置过高的缩减参数。

图3 准确率调节比较(迭代20次)

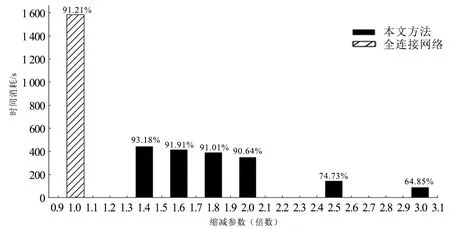
注：准确率显示在时间柱上.%图4 效率调节效果(迭代20次)

图4为不同缩减参数的效率比较，为方便比较将全连接网络时间柱放在1.0处(BP全连接网络无此调节参数)，从图中可以看出全连接网络时间消耗很大，而且准确率也没有明显优势。当反向随机局部投影的神经网络的缩减参数设置为1.4时准确率则优于传统全连接网络2.61%，效率上却大幅提升了272.78%；设置为1.6、1.8接近全连接网络，而效率更进一步提升。

2.3 模型准确率与效率评价

为了方便不同网络规模的定性比较，以下各实验的对比分析采用准确率接近全网络的缩减参数，定为1.8。在实验中，以测试集的分类准确率来比较模型的准确率，使用两种模型不同迭代的曲线图进行对比，如图5所示，以数据集训练和测试时间的总和进行评价模型的效率，如图6所示。

在图5中，反向随机局部投影的算法在迭代次数比较低的情况下，学习效果不全面，因此准确率不理想。随着学习的深入(迭代的增加)学习效果明显提升，在迭代20次的时候已经处于比较稳定的效果和接近全网络模型。

图5 准确率比较(不同迭代)

在图6中，在相同的迭代的情况下效率，可看出传统的全连接网络效率低下，在迭代20次的时候，两种网络的准确率基本一致的情况下，本文方法时间消耗却能节省353.8%。在时间消耗上，本文方法迭代100次比全连接网络迭代20次还低，准确率从91.2%(全连接网络迭代100次)提升到96.4%(本方法迭代20次)。随着迭代的增加，本文方法所体现出来的效率优势越来越明显，时间差距也越来越大。

图6 效率比较(不同迭代)

实验表明，迭代20次以上时，本方法和全连接网络准确率已经基本接近，而本方法的效率却大幅提升，在同等时间消耗情况下远优于传统全连接网络训练准确率。以局部网络迭代20次为例，其准确率已经达到90%以上，超过了全连接网络的迭代6、10次的效果，时间却节约了一半，以迭代20、50次为例对性能提升详细比较如表3所示。

从表3可见，反向随机局部投影算法的平均准确率虽然只提升3.48%，但平均效率提升却十分明显，具有明显的效率优势，而且在保证准确率的同时，效率提升有效。另外，本算法可以根据不同数据集进行参数调优，进一步体现了算法的伸缩性。

3 结论

1)本研究提出的反向随机局部投影，可以按缩减参数调节网络规模，随着缩减参数的增加而增少，其模型效率提升，但准确率也会下降，反之也成立，当缩减参数为1.0时则模型和全连接网络一致。

2)随机局部连接算法是基于BP神经网络模型中的全连接网络基础上，在改进效率的同时保证了准确率。实验中，算法充分体现了其性能的优越性，准确率、效率分别平均提升了3.48%和105.21%，缩减参数同时提升了模型的可适应性。

3)模型与数据集可以在训练中寻找缩减参数最佳值，但局部网络普遍存在信息丢失问题，与全连接网络的准确率仍然有细微差距，后期研究还需要通过对数据集进行降维、去噪等预处理，从而更进一步提升算法的准确率。