成形砂轮高精度数控修整方法研究
杨小李 郑阳伦 钟 睿 蒋凌霄 陈奕璋 汪中厚 江小辉 吴世青
(上海理工大学 上海200093)
成形磨削时,成形砂轮与工件接触且绕自轴线旋转,从而磨削出整个工件廓形,是一种高效率、高精度、低成本、高利润的磨削加工方法[1-2]。随着新型材料与复杂形状曲面工件使用的增多,以及市场对高精度、高效率、低成本的生产要求的提高,成形磨削技术得到了前所未有的快速发展[3-5]。成形磨削技术通常包括往复式成形磨削、缓进给强力磨削、连续修整成形磨削、电镀超硬磨具等[6-7]。其中运用最广的是往复式磨削方法,其磨削进给量在不同磨削阶段都会变化,精磨一般在 0.01mm 左右,而粗磨削一般在 0.05mm 左右。该磨削方式具有高效率、高表面质量、高经济性等加工特点,这使得该磨削方式常用来磨削超硬或难加工材料,一般运用于磨削面简单、待磨削量小的场合[8]。缓进给强力磨削的进给量很小,是一般磨削几十分之一,磨削深度可达 30mm,因而该磨削方式在所需纵向进给量小而磨削深度大的场合具有一定优势。由于其较深的磨削和低进给量磨削,因而高金属切除效率、高精度、高表面质量等特点,但与此同时,因切削面积大而厚,存在发热量大、工件易烧伤等问题。故较好冷却方式是必不可少的,此方式常运用于短时间磨削、中等切除量的场合[9]。连续修整成形磨削以其高效率磨削特点而被广泛运用,又称 CD 成形磨削。该磨削方式利用金刚石滚轮对砂轮进行接触式修整,修整的砂轮磨削效率高、精度高,适用于磨削面多、高效高精磨削场合。为了适应自动更换砂轮和工件多品种少批量高效生产的需要,CD成形磨削不断朝 FMS自动缓进磨削系统发展。另外电镀超硬磨具(如 CBN 砂轮)在超高速高效磨削技术中的应用与发展日新月异,其以超高磨削线速度、磨削效率、金属切除率等优势被广泛运用于各种齿轮加工[10]。目前,在成形磨削技术领域,国外许多研究学者取得了较大进展,如德国 Gubing 自控公司的 FD612磨床上可在很短时间内(70s)完成磨削加工铬锰钢齿轮,可见其经济性之好、效率之高[11]。日本机械技术研究所为解决磨削过程中烧伤等问题发明了一种电镀砂轮,显著降低磨削热等冷却问题[12]。德国KAPP 公司研制的主轴转速高达62 000 r/min 的磨床已经运用于磨削加工叶片棒开槽[13]。
可知,国内外成形磨削技术发展迅速,磨削加工速度、效率、精度等都在不断提高。超高硬度材料、复杂难加工零件的出现以及市场对高精高效加工方式的迫切需求,推动了成形磨削技术的发展。在成形磨削中,决定其磨削精度的关键技术是成形砂轮的修整,下文将分析研究两种主要的成形砂轮修整方法。
1 直线插补修整
空间直线插补是在已知该直线始末两点的位置和姿态的条件下,求各轨迹中间点(插补点)的位置和姿态。大多数情况下,机器人沿直线运动时姿态不变,所以无姿态插补,即保持第一个示教点的姿态。空间直线插补如图1所示,已知直线始末两点的坐标值p0(x0,y0,z0) 、pe(xe,ye,ze) 及姿态,其中p0, pe是相对于基坐标系,这些位置和姿态通常是通过示教方式得到的。设v为要求的沿直线运动速度,Ts为插补时间间隔。
为减小实时计算量,示教完成后,可求出以下数值。
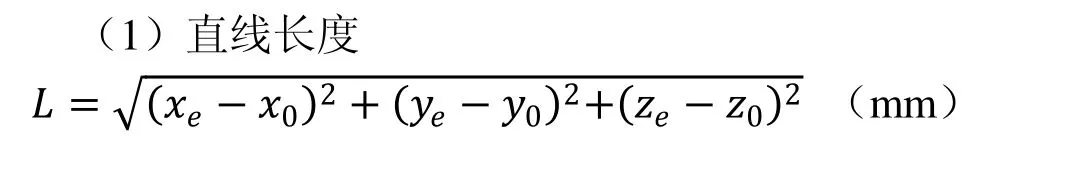

于是可以实时计算各插补点坐标值
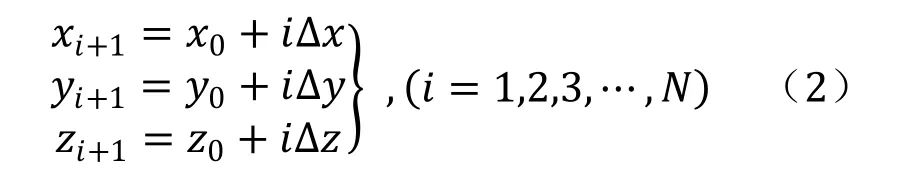
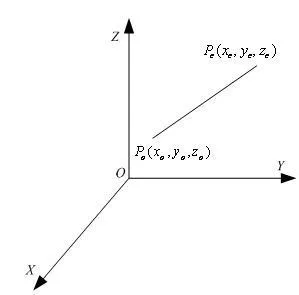
图1 空间直线插补
2 样条插补修整
对于某些复杂零件,当无法通过基本的直线、圆弧以及其它的二次曲线形式来描述其轮廓时,可以通过离散表格或高次曲线给出。为此,在有些高档 CNC系统中设置了相应的插补方法,而下面介绍的三次样条插补方法就是其中的一种。
2.1 三次样条插补基本原理
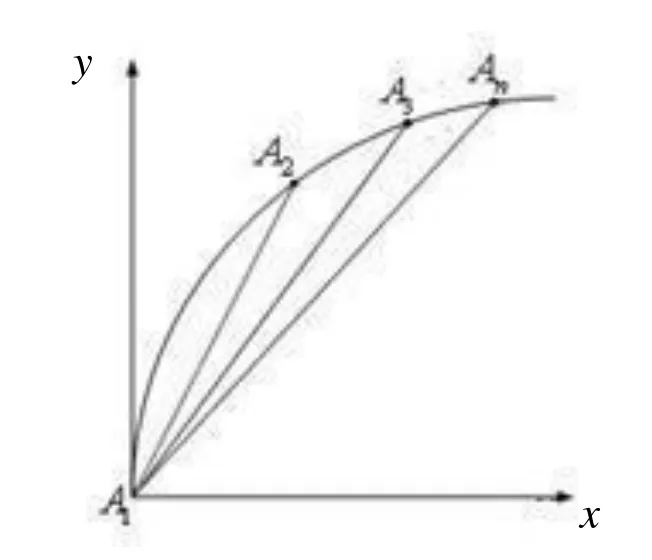
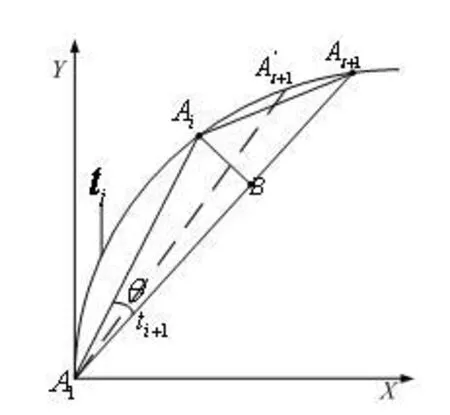
三次样条函数定义:已知n个离散点为P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),且x1 (1)曲线通过所有型值点,即S(xi)=yi(i=1,2,3,…,n) ; 三次样条函数广泛应用于给定型值点的曲线拟合等研究领域。根据被插补高次曲线给出一定数量的型值点,用三次样条函数求解出插补中间点,无疑是高次曲线插补的一种思路。但是,若要将三次样条函数直接应用于高次曲线的插补,则必须满足三次样条函数定义的所有条件。事实上,由于插补前给出的型值点已经是被插补高次曲线上的点,当然也基本能满足相应的三个条件。但是型值点自变量区间的划分条件并非都能得到满足。这是由于机床加工任何轮廓曲线过程中均有两种加工方向,如图 2所示零件轮廓曲线,当起点在A1(x1,y1) ,终点在An(xn,yn) 时,可以满足区间划分条件x1 图2 加工方向示意图 针对这些情况,为了应用样条插补,就必须对有关条件进行处理,主要包括如下几个方面: (1)设定合适的坐标原点。一般情况下,为了简化计算过程,大多将插补坐标系的原点平移到第一个型值点(x1,y1) 处。 通过选择上述弦长作为参数,降低了对于单个坐标轴x或y的单调性要求,从而使大部分曲线均能满足样条插补的条件。 图3 弦长参数示意图 (3)进行合适的分段处理。当经过上述两步处理后,如果在整个型值点区间上仍不能满足弦长递增这一条件,可将整个区间进行适当的分段处理,以保证在每一段内均能满足弦长递增的条件,然后分段插补即可构成整个零件轮廓。 显然,以(ti,Xi)(i=1,2,…,n) 构成的三次样条函数X(t) 严格经过Xi(i=1,2,…,n)点,以(ti,Xi)(i=1,2,…,n)构成的三次样条函数Y(t)严格经过Yi(i=1,2,…,n)点。可以证明:在1,2,…,n−1区间内,以t为参数,Xit,Yit构成的参数三次样条函数虽不满足三次样条函数的能量极小性,但仍具有连续的一阶导数和二阶导数。 现根据每一步插补的弦长增量∆t ,由参数三次样条函数计算出相应坐标轴增量∆x和∆y,即可完成高次曲线的插补。下面可以证明,通过适当选取弦长增量∆t,不需要复杂的实时计算,即可保证每一个插补周期内的插补步长恒定,同时可达到很高的插补精度。 如图 4所示,设有两个相邻插补点分别为Ai(xi,yi),Ai+1(xi+1,yi+1) ,它们对应的弦长参数为,现假设Ai和Ai+1即为插补点,则步距角θ=∠AiA1Ai+1,进给步长为。由于插补周期Ts 很小,所以用弦来代替曲线AiAi+1实行插补进给,其间的误差仍是允许的。 图4 样条插补示意图 为了求出式(6)所示三次样条函数中的系数 ,自定义: 则由三次样条函数一、二阶函数连续的条件,可以推导出如下关系式: 显然,根据式(6)可以得到(n−2) 个线性方程,如果再补充两个端点条件,则可采用各种数值计算方法求解出式(6)中的系数Ai,Bi,Ci,Di。一般给的端点条件有: 然后根据加工零件的有关情况,选择相应的端点条件补充到式(9)中去即可。同理,可求得式(7)中的系数。在求得上述系数后,即可根据弦长参数 所在区间段,由式(6)和式(7)求得插补点坐标值xi, yi和对应的坐标增量值∆xi,∆yi。 通过以上分析可以看出,三次样条插补方法是属于数据采样方法中的一种,并且其插补计算量相对其它插补算法来讲是相当大的,这也对 CNC系统中CPU处理速度提出很高要求。但是,目前计算机处理速度已经取得迅速发展,为样条插补算法的实现提供了保证。 总之,在其他插补方法无能为力的时候,采用三次样条函数进行插补无疑是极为有效的补充手段。 前面介绍了两种数控插补方案,本文采用NUM Flexium68数控系统进行实验,此系统提供直线插补和样条插补功能,所以通过实验对这两种插补方法进行比较。分别对砂轮进行直线插补修整与样条插补修整并进行磨齿实验,磨齿效果如图7所示。 图7 插补修整对比 图7(a)为直线插补修整磨齿后的齿面情况,图7(b)为样条插补修整磨齿后的齿面情况,两次磨齿采取相同的磨齿工艺,公法线去除量、粗磨精磨进刀量与进刀数、砂轮线速度、砂轮冲程速度等都相等。对比可以看出,样条插补磨齿后的齿轮表面更光顺,而且经检测之后发现,样条插补磨齿后的齿廓形状偏差较小,因此可以得出结论,相同的磨齿工艺下,样条插补磨齿精度比直线插补要高。 本文研究了成形砂轮直线插补修整和样条插补修整的基本原理与基本算法,然后采用这两种插补方法分别对砂轮进行直线插补修整与样条插补修整,并且进行磨齿实验。实验结果表明,相同的磨齿工艺下,样条插补修整磨齿精度比直线插补修整要高。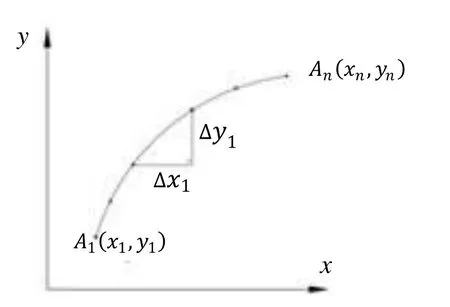

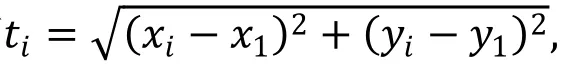

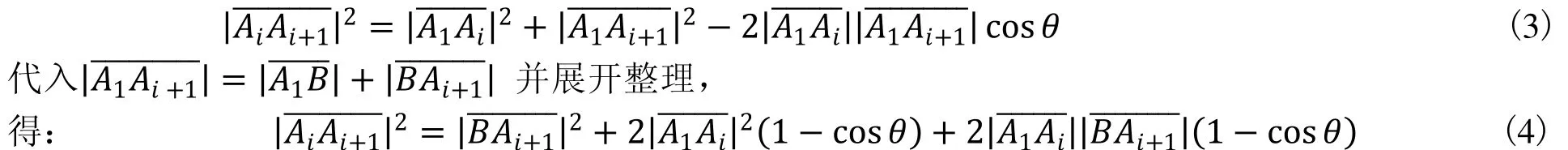


2.2 三次样条插补基本算法
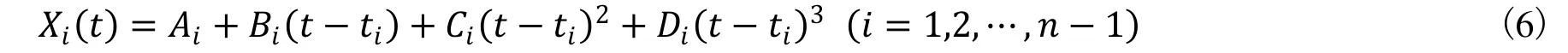
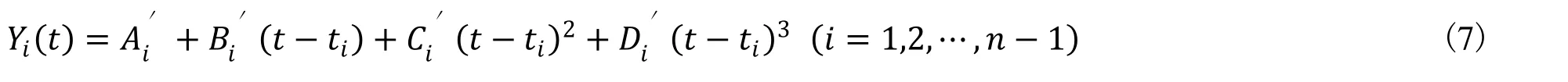

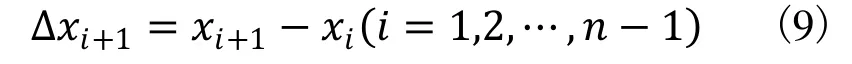
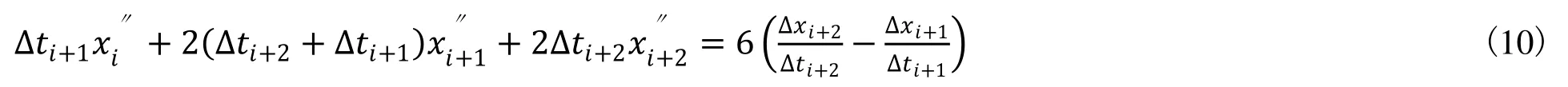

3 实验

4 结语

