基于位编码链表的快速频繁模式挖掘算法研究

顾军华，苏 鸣，张亚娟，张丹红

1.河北工业大学 人工智能与数据科学学院，天津300401

2.河北省大数据计算重点实验室，天津300401

1 引言

频繁项集挖掘是数据挖掘领域中重要的研究方向之一，其最初的用途是分析超市购物篮[1]，通过交易数据，来获得顾客对不同商品的购买习惯，帮助商家制定销售策略。在过去20 年中，频繁项集挖掘一直是数据挖掘领域的热门研究课题，且广泛应用于气象关联分析、银行金融客户交叉销售分析[2]和电子商务搭配营销等[3]领域。

频繁项集挖掘的经典算法Apriori算法是由Agrawal等人[4]于1994年提出的。该算法基于先验原理，简单易懂，但效率低下，面对数据库中的巨量数据，由于其算法存在产生大量候选项集，以及需要重复多次扫描数据库的问题，会对内存产生巨大的负载。对此，提出了一系列的改进算法。2000年，Han等人[5]提出基于FP-tree的FP-growth算法，该算法以FP-tree作为数据结构，在挖掘过程中只需要扫描两次数据库，并且不生成候选项集，相比于Apriori 算法的挖掘效率有很大的提升。基于FP-growth 算法思想，近年来提出了很多改进算法。2012年，Deng等人[6]提出了PrePost算法，该算法通过对FP-tree进行前序和后序的两次遍历，得到每个节点的前序序列pre-order 和后序序列post-order，并据此构建前序后序编码树（Pre-order and Post-order Code tree，PPC-tree），得到1-项集的节点列表（N-list）。通过迭代连接两个频繁的（k-1）-项集的N-list，可以得到所有的频繁k-项集。2014年，Deng等人[7]提出一种基于Nodeset[8]数据结构的FIN 算法，该算法与PrePost 算法的不同之处在于，构建Nodeset中的节点仅需要FP-tree的前序遍历顺序，并且在挖掘过程中还使用了对搜索树进行优化的超集等价剪枝策略，进一步精简了挖掘空间，增加了挖掘效率。与Nodeset 相比，2016 年，Deng 等人[9]提出的DFIN 算法构建的DiffNodeset 中，每个k-项集(k≥3)的DiffNodeset由两个（k-1）-项集的DiffNodeset之间的差异性生成。由于DiffNodeset 的规模要小于Nodeset，所以DFIN 算法的挖掘效率要优于FIN 算法。2018 年，Biu等人[10]提出了NFWI算法，该算法采用基于N-list改进的WN-list 作为数据结构，用于挖掘加权频繁项集，挖掘效率要高于PrePost 算法；但由于仍需要根据前序和后序编码进行大量交集运算，仅适用于大型稀疏数据集。

FIN 算法的缺点是在对两个Nodesets 进行连接时，需要对编码树（POC-tree）进行多次遍历，并且需要判断两个不同的Nodeset 能否满足连接条件，这会消耗大量时间。而尽管DiffNodeset 相比于Nodeset 具有优势，但对于稠密数据集，计算两个DiffNodeset 之间的差异仍需要较长时间；并且由于使用了差集策略[11]，也会占用较大的内存空间。针对这些问题，提出基于新的数据结构位编码链表（Bitmap-code List，BC-List）的频繁项集挖掘算法（BC-List Frequent Itemsets Mining，BCLFIM），BC-List中的每个节点均采用编码模型—基于集合的位图来表示。通过这种数据结构，在连接频繁（k-1）-项集以得到频繁k-项集的过程中，可以按位运算，避免了大量交集运算。此外，该算法还使用集合枚举树来代表搜索空间，并且使用超集等价和支持度计数剪枝策略来对集合枚举树进行剪枝处理，减少了空间占用，提高了频繁项集的挖掘效率。

2 问题定义

2.1 基本概念

表1 事务数据库DB

定义2（频繁项集）若项集A的支持度大于最小支持度minSup(∈[0，1]），即support(A)≥minSup，则称A是频繁项集；如果A的长度为k，则称A为频繁k-项集。

根据定义1 可以计算表1 所示的事务数据库DB 中的1-项集的支持度计数，如表2 所示。设minSup为0.4，则由定义2 可得频繁1-项集为{a},{b},{c},{d},{e}。将每个事务中非频繁项删除，然后按支持度计数将事务按非升序排列，如表1所示。

表2 1-项集及其支持度计数

2.2 构建BC-tree

图1 表2中频繁项的索引

定义6（Bitmap-Code（BC）项集位图代码）设存在任意一个项集P，项集P可以用大小为nf的位图代码BC(P)=bnf-1…b1b0来表示。项索引L1中的第j个项与位图中的bj相对应；若项i(i∈L1)是P中的成员，那么位图中根据定义5的项索引，相对应的位置为1，否则置为0。例如，根据表2得到的位图如图2所示。

图2 表2中每个频繁项所分配的位

对于表2 中的1-频繁项集{b}，其位图为BC({b})=01000，如图3所示。

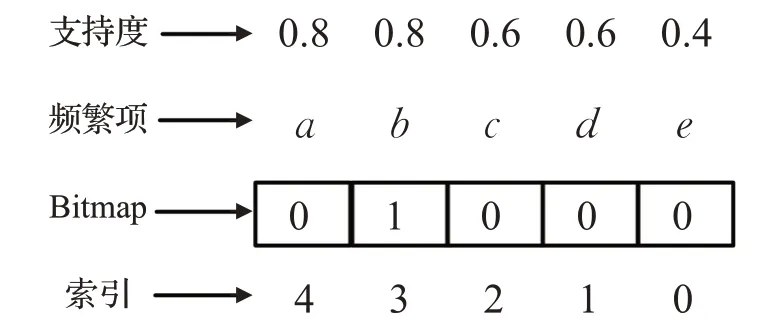
图3 频繁1-项集{b}的位图

输入：事务数据库DB，最小支持度minSup。

输出：BC-tree，频繁1-项集L1。

1.扫描事务数据库DB，找到频繁1-项集F1；

2.根据定义3 将F1中的项根据各项支持度按非降序排序；

3.创建BC-tree的根节点Tr，并执行以下初始化任务：

图4 根据表1的事务数据库构建的BC-tree

2.3 构建BC-List

根据BC-tree，可以得到频繁1-项集。在定义BCList之前，首先给出BC-List中节点信息BC-N-info的定义。

定义8（BC-N-info）设N是BC-tree中的一个节点。节点N的BC-N-info，由节点的bitmap-code 和count 组成，即（N.bitmap-code，N.count）。

定义9（BC-List（频繁1-项集））给定一个BC-tree，频繁1-项集的BC-List是在BC-tree中所有节点的BC-N-info的集合，按BC-N-info.bitmap升序排序。项集{a}的BC-List，BCL（{a}）={（10 000，4）}。得到的频繁1-项集的BC-List如图5所示。

图5 根据图4生成的频繁1-项集的BC-List

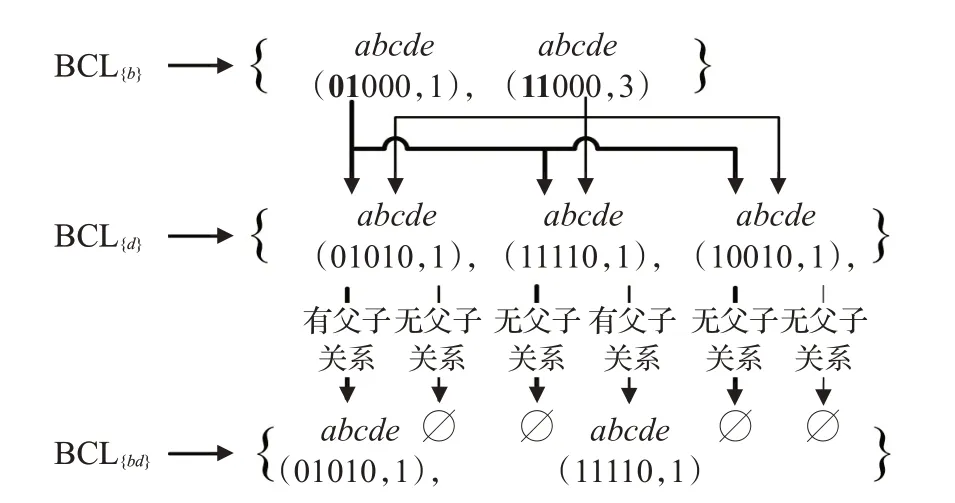
图6 频繁1-项集的BC-List连接

3 基于BC-List的BCLFIM算法

BCLFIM算法在挖掘频繁项集的过程中，通过扫描BC-List，连接两个满足最小支持度条件的频繁（k-1）-项集来发现频繁k-项集，以生成新的BC-List，并得到频繁k-项集的支持度。为了避免重复连接的问题，BCLFIM算法使用了集合枚举树来代表搜索空间。在搜索过程中，使用了超集等价策略和提前停止交集策略来对搜索空间进行剪枝操作，进一步缩小了算法的时间复杂度，提高了挖掘频繁项集的速度。

3.1 剪枝策略

BCLFIM 算法使用集合枚举树[12]来代表搜索空间，利用集合枚举树的特性来避免在挖掘频繁k-项集时出现重复连接的问题。在根据集合枚举树构建BC-List的过程中，为了提高挖掘频繁项集的速度，还对搜索空间使用了超集等价策略[13]和支持度计数剪枝策略[14]来进行剪枝操作。

3.1.1 集合枚举树

输入：节点N，N的父节点生成的频繁项集BCLparent。

输出：频繁k-项集BCLN。

图8 根据表2构建的集合枚举树

3.2 BCLFIM算法描述

BCLFIM 算法可分为以下几个步骤：（1）扫描事务数据库DB，将每个事务的项集按支持度以非升序排序，得到频繁1-项集F1，构建频繁1-项集F1对应的BC-tree。（2）通过扫描BC-tree，得到频繁1-项集F1对应的BC-List。（3）根据算法2，在集合枚举树所代表的搜索

4 实验

4.1 实验环境

为了避免其他客观因素带来的性能差异，将3 种用Java 语言编写的算法[17]在同一台内存为8 GB，CPU为Intel®Core ™i5-2430M@2.40 GHz，操 作 系 统 为Windows 10专业版的PC上运行，以保证实验结果是公平有效的，如表3所示。

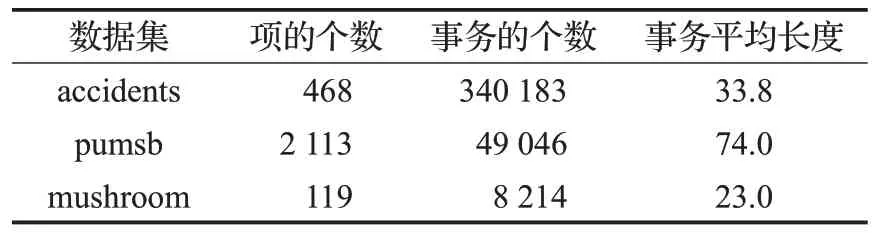
表3 实验使用数据集及其特征

给定相同的最小支持度与相同的数据集，发现通过BCLFIM 算法挖掘得到的频繁项集与FIN 算法和DFIN算法挖掘得到的频繁项集相同，证明了BCLFIM算法所挖掘的频繁项集的正确性，如表4所示。

表4 mushroom数据集下频繁项集数量

4.2 实验分析

3 种算法在如表3 所示的3 个不同数据集下运行时间对比，如图9 所示。在稠密数据集pumsb 和accidents中，BCLFIM 算法相比于FIN 算法有明显的效率提升，相比于DFIN算法运行时间也相对缩短。在稀疏数据集mushroom 中，由于数据集规模较小，结果区分并不明显。但也可看出BCLFIM 算法比其他两种算法的运行速度也相对更快，表明BCLFIM算法在不同的数据集上均具有较高的时间效率。

图9 不同数据集上3种算法运行时间对比

图10 是3 种算法在3 个不同数据集下的内存占用对比。由图10（a）和（b）可以看出，虽然在数据集较大时，BCLFIM 算法的内存占用要大于FIN 算法，但是始终小于DFIN 算法。图10（c）表现在mushrooms 数据集上的3 种算法内存占用情况，由于数据集稀疏，挖掘过程中消耗内存较少，所以3种算法的内存占用变化不明显，但可以看出BCLFIM算法的内存占用相对较小。综合来看，BCLFIM算法也有较高的空间效率。

图10 不同数据集上3种算法内存占用对比

实验表明，本文提出的BCLFIM算法对稠密数据集和稀疏数据集同样适用。相比于FIN算法，由于使用了新的数据结构BC-tree，无需对树进行多次遍历，就可以得到节点信息列表BC-List，通过BC-List就可以得到两个节点之间的祖先-后代关系，大大减少了生成频繁k-项集的时间。相比于DFIN 算法，BCLFIM 算法的连接过程更加简单，项集支持度的计算也更加便捷。除此以外，BCLFIM算法还使用了超集等价和支持度计数剪枝策略来对频繁k-项集的生成进行优化，在内存占用较小的情况下，加快了挖掘频繁项集的速度，提升了挖掘效率。

5 结束语

本文提出的BCLFIM算法，使用基于位图编码表示的节点编码模型生成位图树（BC-tree），以BC-tree 的节点信息作为数据结构，通过按位运算来快速获取BCList的节点集合，并通过两种剪枝策略来缩小挖掘频繁模式的搜索空间，解决了FIN算法由于存在建树过程复杂及支持度计算繁琐而导致的挖掘效率较低的问题。通过实验对比FIN 算法与DFIN 算法，证明了本文提出的算法在内存占用与运行时间上表现更好，具有较高的挖掘效率。

在接下来的研究中，将结合分布式计算理论，对该算法进行进一步优化，以应对当前大数据时代背景下的海量数据。除此以外，拟将该算法应用于气象领域，尝试挖掘空气质量要素与气象要素之间的关联性，充分发挥算法的应用价值。