具有动态自适应学习机制的教与学优化算法

李丽荣，李木子，李崔灿，王培崇

1.河北地质大学 艺术设计学院，石家庄050031

2.河北地质大学 信息工程学院，石家庄050031

3.河北地质大学 人工智能与机器学习研究所，石家庄050031

1 引言

群智能[1-3]算法是通过模拟生活中的自然现象或某些动、植物群体间竞争、协作进化等行为，实现对优化问题的求解。Rao 和何雨洁等人[4-5]提出的教与学优化（Teaching and Learning Based Optimization，TLBO）就是具有代表性的群智能算法之一，且已被应用于多个工业或学术领域。如：Data Clustering[6]，生物医学中的TDC时间数字转换器的优化[7]，工业机器人装配序列规划优化[8]，拆卸服务生产线中的服务平衡优化问题[9]，集合联盟背包问题[10]等。

在TLBO 算法中，标记最优个体为“教师”，其他个体为“学生”，通过模拟一个班级中的“教”和“学”两种行为，实现对问题的求解。算法原理简单、参数较少、易理解，且收敛速度较快。但是，相关的研究表明，当待优化问题的维度较高时，该算法也容易出现收敛速度变慢、陷入局部最优等弱点[10]。为了克服算法的这些弱点，改善其性能，文献[11]提出了一种改进算法（ICTLBO），该算法将种群划分成多个子种群。“教”过程中，个体通过所在子种群的平均位置和教师个体间的差异信息，被引导着向全局最优所在区域收敛。同时子种群间实施信息交换，以逃离局部最优的约束。在“学”阶段引入了全新的学习机制，提高种群的多样性，并设计了针对三种不同约束情况的处理策略。文献[12]在TLBO中引入多教师，并将“教”过程中的TF参数修改为自适应变化，同时又引入了讨论学习和自我激励学习机制。一系列的实验表明，算法改进后效果明显。文献[13]在TLBO 中引入局部学习机制和自适应学习机制，以提高算法的搜索能力。在“学”阶段，当前个体不仅向种群内的最优个体学习，而且也向随机产生的个体学习。在自我学习阶段，当前个体要么依赖自身的梯度信息更新自身状态，要么依据种群的平均位置和个体的差异度，随机勘探新位置。迭代多次后，所有的个体重新排列。于坤杰等[14]针对TLBO算法中种群间缺少信息交流和反馈的问题，提出了一种精英反馈学习机制，利用精英个体的强反馈能力引导种群内状态较差的个体快速收敛。王滔高等[15]提出了一种基于种群结构分层的改进机制。将学生种群依班级的平均成绩划分为多个等级层次，种群的进化状态自底向上更新，有效缓解了算法易陷入局部最优的问题。张琳琳等[16]提出了一种基于四边形网状元胞自动机模型来处理种群的邻域和种群更新规则。何杰光等[17]提出将个体分为全局和局部两种维度。种群内的个体采用全局维度和局部维度混合更新，并设置两种权重动态调整更新的维度数量。后期引入自我学习机制，强化搜索最优个体周边和边界信息。文献[18]提出了一种应用经验信息和变异操作的改进TLBO 算法。参考DE算法的变异操作，在“教”和“学”两个阶段引入不同的变异操作。文献[19]在精英教与学优化算法基础上提出了一种具有多教师和自我激励学习的改进TLBO。文献[20]在TLBO中引入基于个体差异的自主多机制学习，同时令当前个体执行融合高斯搜索的反思机制，协助其跳出局部最优的约束。

为了克服标准TLBO算法的弱点，本文提出了一种具有自适应学习的教与学优化算法，在“教”算子中引入非线性自适应变化的学习因子δ，以克服算法的早熟。算法后期令教师个体执行动态随机搜索（Dynamic Random Searching，DRS）策略，加强最优个体勘探新解的能力。

2 教与学优化算法

标准教与学优化算法有两个主要算子，分别是“教”和“学”。

3 动态自适应教与学优化算法

3.1 动态自适应学习

TLBO算法思想源于模拟班级的教学过程，所以从生活中的现象着手改进算法是一种可行的途径。考虑在教师的“教”过程中，学生新状态的生成取决于自身状态的转化比例和通过学习所获得知识的转化比例之和。而标准算法中公式（1）的rand(0,1)×(Xt(t)-β×Xm(t))部分为学生向教师学习获得的知识，而该式中学生自身的知识状态完全向新状态转化，与现实情况不相符。故将式（1）修改成为式（3），学生的原状态按比例向新状态进行转换。

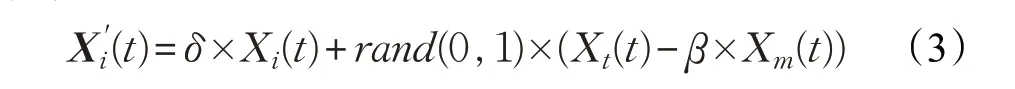
δ=1/(1+exp(k×(T-2×t)/T))∈(0,1)是一个非线性自适应因子，T 为预设最大迭代次数，t 为当前迭代次数，k 为变化速率。很容易看出来，在算法早期，种群主要向教师个体学习，可以快速向最优个体周围靠拢。而随着迭代的进行δ 逐渐增大，个体维持自身状态能力增强，减缓了向最优个体靠近的速度，避免过早的聚集于教师周围。而这种机制也与生活中学生的学习行为一致，在早期学生能力较差时，主要向教师学习，快速提升班级的平均分。后期学生状态提升之后，学生会有选择的吸收教师传授的知识，保持自己状态的能力增强。

3.2 教师的动态随机搜索

DRS 通过动态调整步长实现对个体周围空间的精细搜索。在群智能算法中，种群的最优个体包含了较多的引导种群向全局最优收敛的信息。如果群智能算法能够实现全局收敛，最优个体所形成的搜索空间，一定包含着全局最优解形成的搜索空间。所以，为了提高算法的精度，在算法后期（本文为预设迭代次数的2/3后开始）引入教师个体执行DRS。

算法1DRS算法

输入：个体X，迭代次数n。

输出：个体X。

步骤1 初始化步长d。

步骤2 生成向量X′∈[-d,d]。

步骤4 生成向量X1=X+X′和X2=X-X′。

步骤5 选择X1,X2,X 中优者作为X 。

步骤6 调整步长d。

步骤7 迭代没有结束，则转步骤2；否则输出X ，结束算法。

3.3 算法实现

算法2动态自适应教与学优化算法（Dynamic Selfadapting Learning TLBO，DSLTLBO）

输入：种群规模n，最大迭代次数M 。

输出：最优个体Xt(t)。

步骤1 在解空间内初始化种群POP。

步骤2 挑选出最优个体，即教师个体，标记为Xt(t)。

步骤3 基于公式（3）执行“教”。

步骤4 执行“学”算子。

步骤5 如果是算法后期，则教师个体执行DRS算法。

步骤6 算法不满足终止条件，则转步骤2；否则输出最佳个体Xt(t)，终止算法。

3.4 算法的收敛性

证明分析DSLTLBO中个体Xi(t)的搜索。算法早期，“教”算子执行过程，该个体主要向Xt(t)学习，即向最优个体靠近。这种能力，随着δ 的逐渐增加而被抑制，Xi(t)保持自身状态的能力逐渐加强，丰富了种群多样性，减轻了“教”算子带来的过早的收敛压力。算法后期，Xt(t)开始执行DRS 算法，加强搜索周围的局部空间，算法全局、局部搜索得以平衡。DSLTLBO中的“学”算子，赋予了Xi(t)跳出局部最优约束的能力。

不失一般性，以最小化问题min f(X)为研究对象。设解空间A 内有s 个局部最优区域A1,A2,…,As，则DSLTLBO迭代过程中，个体Xi(t)负责区域Ai的搜索，据引理2 知，Xi(t)必收敛到该区域的最优值Yi。由于Xi(t)执行“学”，随机向某一个同伴Xk(t)学习，所以会搜索该个体所在空间Ak(t)。类推可得，所有局部最优区域会被依次访问，且可保证收敛到相应的局部最优值，将它们分别标记为：X1b(t),X2b(t),…,Xsb(t)。

由于采取保优策略，如果迭代次数足够多，则Xgb=min{X1b(t),X2b(t),…,Xib(t)} 必然会收敛到全局最优，即DSLTLBO算法能够以概率1收敛到全局最优。

3.5 算法复杂度分析

设算法的迭代次数是M ，种群规模n，则算法的时间复杂度是O(M×n) ，空间复杂度是O(n) 。可以看出，本文的算法并没有增加TLBO的时间复杂度和空间复杂度。

4 仿真实验与分析

4.1 实验环境及参数

为了验证算法的性能，基于C 编程实现DSLTLBO算法，并选择了文献[22]中的10个基准函数进行性能测试，分别是：f1：sphere、f2：Rastrigin、f3：Schwefel、f4：Rosenbroke、f5：Griewank、f6：Ackley、f7：Quadric、f8：Schwefel、f9：Six-Hump Camel-Back、f10：Schaffer。除f9最优值是-1.031 628 5，f10的最优值是-1，其余函数的最优值均为0，函数维度设为30 和100。选择了DE、PSO、AFSA、TLBO[4]、ITLBO[12]、FETLBO[14]、HSTLBO[15]等算法来做对比，DE、PSO、AFSA是较为典型的群智能算法，其他为近年来出现的典型TLBO改进策略。

算法的参数设置：函数维度为30时，所有算法的种群规模均为30，迭代次数为500次。函数维度为100时，种群规模为50；迭代次数设为f1：1 000次，f2：1 500次，f3：1 000 次，f4：1 000 次，f5：2 000 次，f6：1 500 次，f7：1 000 次，f8：1 000 次，f9：2 000 次，f10：2 000 次。函数的评价精度为：f1～f8：10-6，f9和f10的精度为：10-3。为了对比公平，且忽略掉其他因素的干扰，算法都独立运行30 次。DE、PSO、AFSA 参数均参考相关文献设置。

4.2 实验结果分析

表1 和表2 分别列出了函数维度是30 和100 时，参与对比实验算法的解精度和解方差。当函数维度为30时，f1是一个比较容易优化的单峰函数，此时的FETLBO算法表现最优，DSLTLBO 和HSTLBO 算法稍逊，但是比较ITLBO、TLBO、DE 三个算法有较大的优势。对于f2、f4两个多峰函数，本文的DSLTLBO 算法表现是最优的，在其他的几个多峰和单峰函数上的表现，或者稍逊于HSTLBO 或者稍逊于FETLBO，但是总体要强于ITLBO 等算法。f9、f10是两个比较难以优化的函数，需要算法具有较好的跳出局部最优约束的能力，DSLTLBO算法的表现还是很优秀，和FETLBO、HSTLBO两个算法在精度和解方差上旗鼓相当，要较ITLBO、TLBO 算法的解精度高出了很多。另外，观察表1 中各个算法的解方差，可以看出DSLTLBO 算法的稳定性在f1、f6、f7、f9、f10上是最好的。

表1 30维时算法在Benchmark函数上的运算结果（均值/方差）

表2 100维时算法在Benchmark函数上的运算结果（均值/方差）

当待优化函数维度增加为100时，对群智能算法摆脱局部最优约束的能力要求更高，同时对算法后期勘探新解的能力要求也有所增加。对比表2 和表1 的数值，可以看出，参与对比算法的解精度和解方差均有所下降，横向对比可以看出TLBO、DE、AFSA、PSO四个算法相对下降较多，对比算法中的FETLBO、HSTLBO、DSLTLBO 相对下降较少；DSLTLBO 的解精度在f1、f2、f3、f8四个函数上表现最好优于其他算法，在f6、f7、f9、f10上和HSTLBO、FETLBO 算法基本一样。但是f4、f5两个函数上的表现稍差，略逊于FETLBO 和HSTLBO算法，但差距也并非太大，DE、TLBO、ITLBO算法要明显逊色于这三个算法。从解方差上看，本文中提出的DSLTLBO算法处于前列。

在表3 中，给出了30 次独立运算中的成功次数，可以看出，无论是较低维度还是较高的维度，DSLTLBO算法均具有较高的成功率。为了更好地展示算法在收敛速度等方面的优势，绘制了部分算法在f1～f6函数上的收敛曲线，分别为图1～图6，绘图工具为WPS2019个人版。从六个图的收敛曲线可以看出，DSLTLBO 算法的收敛明显优于其他算法，通常都能经过1 000或2 000次迭代，即可快速收敛到最优解周围，从而进行精细搜索。TLBO算法则在几个函数上存在跳跃点，而且收敛曲线较平直，DE 算法也存在此问题。ITLBO 算法收敛较好，在f5的收敛较DSLTLBO 算法快速，但是在其他函数上的收敛速度均输于DSLTLBO算法。

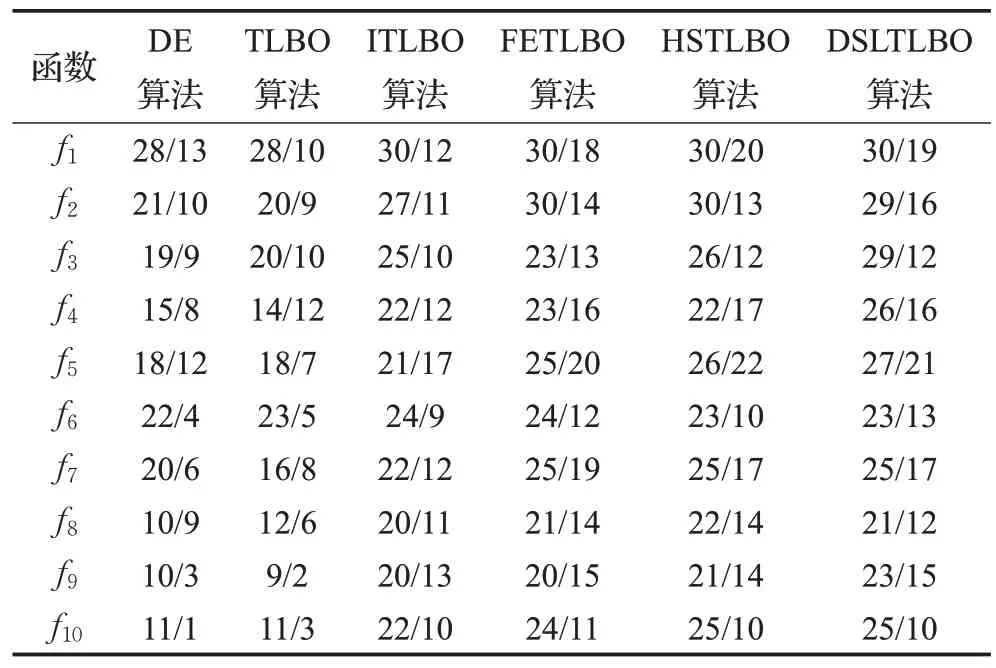
表3 算法的收敛成功次数对比（30维/100维）

综合以上的对比结果，可以看出DSLTLBO 算法的鲁棒性和勘探新解的能力均较优秀。之所以如此，得益于其自身的演化理念和种群的竞争合作方式。算法迭代初期，“学生”主要向“教师”学习。因为δ较小，所以学生个体主要向教师个体学习，快速向最优解周围收敛，有利于算法的收敛速度。算法的中期，学生个体保持自身状态的能力增强，放缓了向“教师”个体靠近的速度，算法全局搜索占据主要地位，可以较好地发现未知的新解。算法进入迭代后期，教师个体开始执行DRS算法，加强对于最优周围空间的精细搜索，提升算法解的精度。同时，种群内的其他个体保持自身状态的能力继续增强，使种群具有一定发散性，避免被局部最优约束，出现早熟。从收敛曲线图可知很直观的看到，DSLTLBO 算法的收敛曲线下降非常快，种群跳出局部最优约束的能力也较好。

4 结论

针对TLBO算法的弱点，本文提出了如下两方面的改进。

（1）在“教”阶段，引入了自适应学习因子δ，该因子在（0，1）区间内非线性逐渐变化，以使种群在早期快速向最优个体周围空间收敛，而在后期种群多样性得以保持，平衡算法的局部搜索和全局搜索。

（2）为了提高算法的求精精度，在算法的后期令教师个体执行DRS 算法，强化对教师个体周围区域的精细搜索。

利用马尔科夫链技术分析了该算法的收敛性，并在10个经典的测试函数上进行了相关实验。实验表明本文提出的DSLTLBO算法具有较好的收敛速度和求解精度，比较适合于求解较高维度连续型的数值优化问题。作为一种具有较高效率的群智能算法，未来将会借鉴传统演化算法的思想，提高TLBO的效率。探索开拓新的应用领域，也是主要的研究方向之一。