改进Hoeffding不等式的概念漂移检测方法

徐清妍，何 丽，朱泓西

天津财经大学 理工学院，天津300222

1 引言

数据流是一组顺序、大量和快速连续到达的数据序列，如何对数据流进行准确高效的分类是机器学习的研究方向之一[1]。在数据流分类过程中，当数据的特征分布随时间发生变化时，之前训练获得的分类器可能无法适应当前数据的特征分布，从而导致无法准确分类当前数据[2]。由于数据流具有时效性，概念漂移是影响数据流分类性能的重要因素[3]。为了及时发现数据流中的概念漂移，需要在数据流分类过程中进行概念漂移检测，并在发生概念漂移后的数据上重新训练分类器，以提高分类器的正确率。

目前，针对数据流的概念漂移检测方法主要是基于分类错误率分析和多窗口数据比对。1954 年，CUSUM和Ph算法作为概念漂移检测的先锋被提出[4]，这种方法通过计算观测值检测概念漂移。当观测值大于用户定义的阈值时，使用漂移的平均值和警报的差值来判断是否发生了概念漂移。ph 算法作为CUSUM 算法的一个变体，主要用于信号处理领域的变化检测[5]。2004 年，Gama等人[6]提出了DDM算法，该算法通过分析分类器错误率及相应的标准偏差来检测数据流中的概念漂移，在突变漂移上获得了很好的检测效果，但是在渐变漂移上效果不佳，且内存的使用量较大。2006年，文献[7]在DDM 的基础上提出了EDDM 算法，该算法通过监视两个连续错误之间的距离来检测概念漂移，能够有效改善渐变漂移的检测效果。为了减少DDM算法中的内存使用量，文献[8]提出了RDDM 算法，该算法在DDM 算法的基础上丢弃了之前未发生概念漂移的部分旧实例，然后重新计算检测警告和漂移级别，能够有效减小概念漂移的延迟。2015年，文献[9]提出了HDDM算法，该算法使用Hoeffding不等式[10]进行概念漂移检测。HDDM算法使用Hoeffding不等式来设置窗口平均值之间差值的上限，但是，这种算法需要对突变漂移和渐变漂移分别设定不同的阈值。

目前，基于窗口的方法主要使用固定窗口来提取最近流过的数据流段特征，用滑动窗口来提取当前数据流段的特征，并通过分析这两个窗口数据分布的差异来判断是否会发生概念漂移。2007年，Bifet提出了ADWIN算法，该算法使用具有可变大小的滑动窗口来检测概念漂移，有概念漂移时，窗口尺寸减小[11]。这种方法过于灵敏，在噪声点多的情况下，错误率较高。为改进ADWIN存在的问题，文献[12]提出了SEQDRIFT 算法，该算法使用两个窗口来分别描述新数据和旧数据。其中，旧数据使用蓄水池采样的方法进行管理，即一次性从旧数据中抽取固定大小随机样本；新数据使用跟随滑动窗口的方法提取最近的数据。2014 年，Huang 等人[13]利用ADWIN 算法的双窗口思想，提出了SEED 算法。在SEED 算法中，当两个子窗口的统计量比较值大于等于漂移判定的阈值时，即判断发生概念漂移，该方法执行块压缩以消除不必要的切割点合并本质相同的块。

以上这些方法虽然能够较好地检测出数据流分类中的概念漂移，但是均存在一定的检测延迟，并且对概念漂移过于敏感。当数据流中噪声率较大时，概念漂移的误判率也随之变高。在实际应用中，快速准确的检测出概念漂移有助于提高数据流分类的正确率，但是要尽量避免噪声点的影响。

2016年，文献[14]融合了统计方法和窗口方法，提出了FHDDM 算法，该算法使用滑动窗口和Hoeffding 不等式进行漂移点检测。2018 年，文献[15]在FHDDM 的基础上又提出了FHDDMS算法，该算法设置一个长窗口和一个短窗口，并通过两个窗口的叠加来检测漂移点，能够降低检测延迟和误判率。其中，短窗口用来应对突变概念漂移，长窗口用于减少噪声对漂移检测的影响。

基于FHDDM 算法的漂移检测方法虽然获得了较好的效果，但仍存在漂移检测延迟的现象。本文在FHDDM算法的基础上，提出了基于交叠滑动双窗口和Hoeffding不等式的漂移检测方法（New Fast Hoeffding Drift Detection Method，NFHDDM），该方法通过在滑动窗口上使用四分位距来提取当前数据流段的特征，并对FHDDM 算法中Hoeffding 不等式阈值定义进行了改进。实验证明，本文提出的方法不仅能够获得更高的漂移点检测正确率，还能有效减小概念漂移检测的延迟，从而提高数据流分类正确率。

2 FHDDM的基础理论

FHDDM是一种基于滑动窗口的漂移检测方法，该算法在预测结果上设置一个滑动窗口。如果预测结果正确，则把1插入到滑动窗口当中，否则把0插入到滑动窗口中。若t 时刻滑动窗口数据的平均值用ut表示，分类过程中滑动窗口数据的最大均值用um表示，um的调整方法如公式（1）所示：

在可能大概正确（probably approximate correct）学习模型下，分类正确率应该随实例数的增加而增加或稳定，否则，发生概念漂移的可能性会变大[16]。如果um值不变且ut与um之间的差大于预设的阈值时，即判断发生了概念漂移。

FHDDM的漂移检测方法如公式（2）所示：

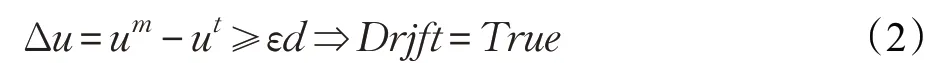
公式（2）中，εd 是FHDDM 定义的概念漂移检测阈值，该值对漂移检测效果具有重要的影响。FHDDM 算法使用Hoeffding不等式（3）来定义阈值εd：

3 改进的FHDDM漂移检测方法（NFHDDM）

3.1 NFHDDM的窗口设定

为了提取到当前数据流段的主要特征分布，本文提出了一种基于四分位距的滑动窗口大小设置方法。四分位距（Inter Quartile Range，IQR）是离散度的一种度量方式，定义为第三个四分位数和第一个四分位数之间的差[17]。若用IQ1表示数据序列中的第一个四分位数的下标，用IQ3表示数据序列中的第三个四分位数的下标，则四分位距窗口数据集DIQR可用公式（5）描述：

在静态数据分析中，通常假定数据是服从同一分布的，但是数据流数据的分布会随着时间而变化。本文使用四分位距设定窗口，即取滑动窗口的四分之一到四分之三范围内的对象进行处理。在窗口滑动过程中，选取的数据可能会把一个完整的概念断开，继而影响概念特征提取的完整性，最终导致分类器性能的下降。四分位距窗口内数据的稳定性说明如图1所示。

图1 窗口解释图

在图1中，滑动窗口中的数据在一定时间后发生了概念漂移，蓝色标记点和红色标记点分别表示两种概念。从图上可以看出，极端异常值通常发生在两个概念的交叠区域，而概念漂移一般存在于该区域中。相较于取整个滑动窗口，四分位距窗口中的数据能够保持当前概念的完整性，降低极端异常值对分类结果的影响，进而提升分类器的正确率[18]。同时，因为四分位距窗口中的样本数更小，还可以减少分类器的运行时间。

3.2 Hoeffding不等式的改进方法

在概念漂移检测中，使用Hoeffding 不等式计算概念漂移检测的阈值。在Hoeffding 不等式中，e-2nεd2中2是一个固定的敏感系数，用于控制模型对概念漂移检测的灵敏度。但在实际应用中，数据流通常是存在噪声的，固定系数难以适应不同噪声率的数据流。为了更好地适应不同噪声率下的概念漂移检测，本文在Hoeffding不等式中引入了动态系数λ，公式（6）和（7）分别描述了改进后的Hoeffding不等式。

将λ引入到四分位距窗口的数据处理中能够更加准确快速地检测到数据流中的概念漂移。在λ的定义中，Pmax相对稳定，当噪声增大时，如公式（8）所示四分位距窗口中数据的分类正确率Pc的值会相应下降，使得λ的值变小，导致公式（7）中的εd增大，从而降低概念漂移检测的灵敏度，减少错误漂移点的检测。反之，当噪声减小时，Pc的值会上升，使得λ的值增大，εd减小，达到提高概念漂移检测灵敏度的目的。

3.3 NFHDDM算法

NFHDDM算法使用滑动窗口和四分位距窗口来检测概念漂移。首先，NFHDDM 需要根据数据流中对象的分类结果来建立滑动窗口。NFHDDM使用的分类器依次对数据流中的每个对象进行分类，若分类正确，分类器输出1，否则输出0，然后将当前处理对象的分类结果添加到滑动窗口。当滑动窗口中的数据个数等于滑动窗口的尺寸时，NFHDDM 根据图1 定义的四分位距窗口，从滑动窗口中截取生成四分位距窗口，并计算Pc，更新Pmax。

若滑动窗口用W表示，四分位距窗口用W_IQR表示，Length(W)用于求窗口W中的数据元素个数，检测到的漂移点的顺序表用Seq_dp[]表示，NFHDDM 的具体步骤如下：

4 实验与结果分析

为了验证本文提出的NFHDDM 算法的有效性，分别在两个不同类型的人工数据集和两个真实数据集上进行了测试，并与数据流分类研究中九个主要的概念漂移检测算法进行了比较。实验环境为Windows7，2.4 GHz CPU，8 GB内存，编程语言python3.6。

4.1 实验设计

4.1.1 实验数据集

考虑到概念漂移包括突变漂移和渐变漂移，实验中使用了两个人工数据集：存在突变漂移的SINE1数据集和存在渐变漂移的CIRCLES 数据集，以及两个真实数据集，各个数据集的主要属性描述如表1 所示。其中，SINE1数据集的分类函数为y=sinx，CIRCLES数据集的分类函数为(x-a)2+(y-b)2=r2。实验中的a、b、r的值分别设为＜（0.2，0.5），0.15＞，＜0.4，0.5），0.2＞，＜（0.6，0.5），0.25＞，＜（0.8，0.5），0.3＞。

表1 实验数据集

4.1.2 评价指标

当发生漂移时，检测算法很难在第一时间检测出来，通常会存在漂移检测延迟现象。为了有效评估漂移检测的及时性，可以对漂移检测的延迟设定一个阈值。当检测出的延迟点数Dj在真实延迟点数Dt阈值范围内则认为正确检测，否则，判定为错误检测。错误率和漂移延迟越小，漂移检测算法的性能越好。本文使用正确率Pc和延迟度wd两个指标来评估算法的性能，计算方法分别如公式（9）和（10）所示：

若当前数据流实际发生概念漂移的次数为m，漂移延迟D的计算方法如公式（11）所示：

4.2 算法性能比较

4.2.1 错误率和延迟度分析

为验证本文提出的NFHDDM算法在错误率和延迟度上的优势，这里选择DDM、EDDM、CUSUM、ADWIN等算法进行了实验比较。为了验证算法的普遍适用性，分别在突变漂移数据集SINE1 和渐变漂移数据集CIRCLES上进行了实验。为了分析噪声对算法性能的影响，实验中在相关数据集中加入了10%的噪声点，实验结果如表2所示。

从表2 中可以看出，在SINE1 数据集上，EDDM 的错误率和延迟度最高，本文提出的NFHDDM 算法在错误率上比表现最好的FHDDMS 算法下降了0.01，漂移延迟度降低了2.75；在CIRCLES 数据集上，NFHDDM算法错误率比FHDDM算法下降了0.06，延迟度也下降了18.67。FHDDM、FHDDMS 和NFHDDM 算法都使用基于Hoeffding 不等式的漂移阈值设定方法，但是，NFHDDM 算法在SINE1 数据集和CIRCLES 数据集上的错误率和延迟度表现均优于其他基于Hoeffding不等式的算法，这主要是因为NFHDDM 算法采用的四分位距窗口能够获得当前数据流段的典型特征，并减少了检测数据的总数，提高了概念漂移检测的及时性。从表2的结果对比中可以看出延迟度越低，错误率也越低。因此，减小延迟度可以有效提升算法的正确率。

表2 错误率和延迟度对比表

4.2.2 噪声对算法性能的影响分析

为了验证NFHDDM 算法对噪声的敏感性，本文通过在两个人工数据集上增加不同比例的噪声进行实验。算法对噪声具有一定的敏感度，当噪声率过大时，应适当考虑对噪声的重新分类而不是忽略不计。图2（a）和（b）分别展示了不同算法在SINE1数据集和CIRCLES数据集上的错误率随噪声率的变化情况。总体上看，在这两个数据集上，噪声率对所有算法错误率的影响基本一致，即噪声率越高，错误率也越高。在对比的各种算法中，EDDM 算法的错误率最高，其他算法的错误率基本一致。同时，从图2 中可以看出，本文提出的NFHDDM算法在不同的噪声率下都能获得最好的错误率结果。

图3（a）和（b）分别展示了不同算法在SINE1 数据集和CIRCLES数据集上的漂移延迟度随噪声率的变化情况。从图3 中可以看出，本文提出的NFHDDM 算法在漂移延迟度上受噪声的干扰最小，漂移延迟度明显低于其他比较算法。这主要是因为NFHDDM 算法使用滑动的四分位距窗口，能够更好地提取当前数据流段的概念特征分布并且引入动态系数能更好的适应噪声对分类器的影响，从而使分类器能够保持较好的稳定性。

4.2.3 算法消融对比分析

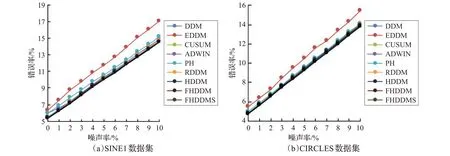
图2 不同噪声率下的错误率对比

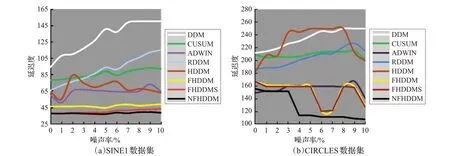
图3 不同噪声率下漂移延迟度对比

为了验证四分位距窗口和动态系数分别对改进算法的影响，本文在数据量较大的人工数据集CIRCLES上做了两个对比实验，选择人工数据集是为了能够明确分辨漂移延迟点。其中，第一个实验FHDDM_IQR只在FHDDM算法中使用四分位距窗口，用于验证四分位距窗口对概念漂移检测的影响；第二个实验FHDDM_λ只在FHDDM算法中引入动态调整系数，用于验证动态系数对概念漂移检测的影响，实验结果如图4所示。从图4（a）和（b）的结果对比可以看出，四分位距窗口对延迟度的影响更大，但是，使用动态系数可以获得更低的错误率，因为动态系数的使用可以更好地适应噪声对分类器的影响。同时，从图4 结果的对比中可以明显看出，只使用四分位距窗口或动态系数都不能获得理想的概念漂移检测延迟度，而结合二者的NFHDDM 算法在分类错误率和概念漂移检测延迟度两个评价指标均获得了最好的结果。因此，在NFHDDM 算法中同时使用四分位距窗口和动态调整系数是必要的。

4.2.4 算法综合性能对比

为了进一步验证NFHDDM 算法在不同评估指标上的整体优势，本文提出了一种基于加权平均的综合性能评估指标方法。对每个数据流，这里使用权重向量W={w1,w2,w3,w4,w5,w6} 计算出一个整体分数Score，向量中的属性分别代表错误率、漂移延迟、假阳性数、假阴性数、内存占用量和运行时间，若用vi表示每个属性赋予的权重，则将Score 的计算方法描述如公式（12）所示：

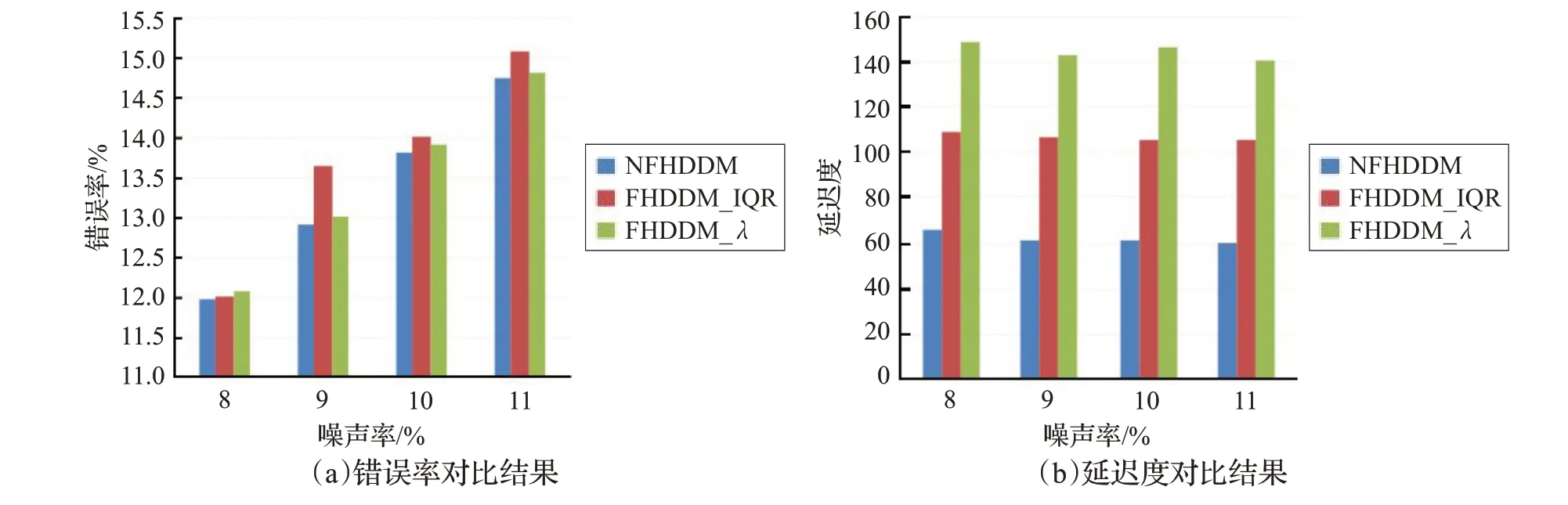
图4 消融实验结果对比

本文为六个属性设置相同的权重，图5展示了在人工数据集上的各个算法的综合性能评估指标分数。从图5可以看出，NFHDDM在综合指标Score上总能保持最优状态，这说明NFHDDM 在定义的六个指标属性上都有上佳的表现，符合上述实验的结果。

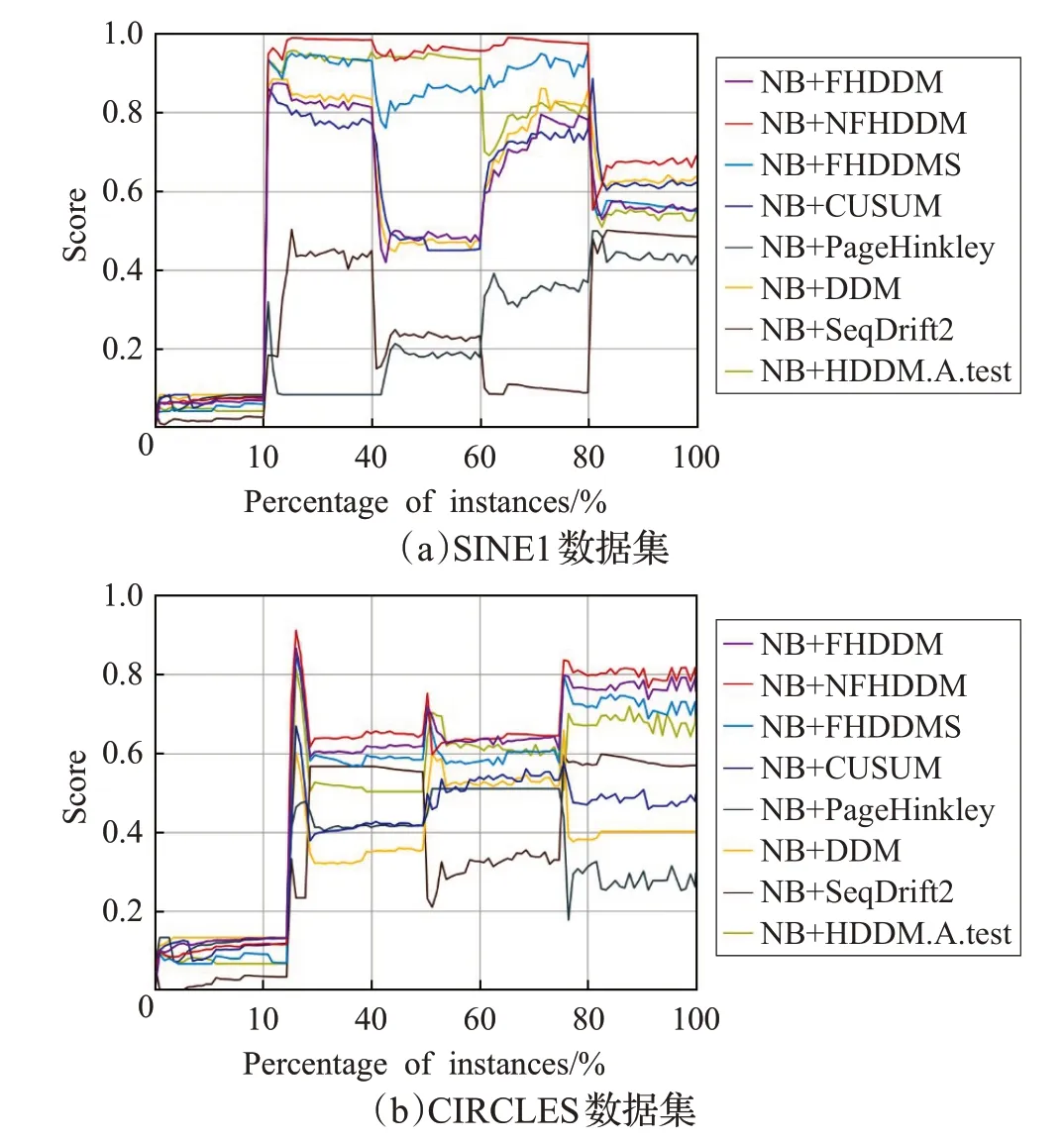
图5 基于人工数据集的综合评估指标分数比较

真实数据集的实验与人工数据集不同之处在于，真实数据集不知道具体的漂移点在哪里，只能通过错误率来验证检测漂移的有效性。同时，在大规模数据流分类应用中，算法运行时的时间效率和内存需求也是影响其性能的重要指标。因此，对真实数据集，本文使用三个综合性能评估属性：错误率、运行时间和运行时占用的内存。并为这三个属性设置相同的权重，各个算法在真实数据集Elecnormnew[19]和Poker-lsn[20]上的综合评估指标实验结果如图6 所示。从图6 的对比中可以看出，DDM、CUSUM 算法Score 分数普遍较低，FHDDM、FHDDMS、NFHDDM 算法分数能够保持在较高水平上，并且，NFHDDM算法的分数总体上处于最高状态。由于Poker-lsn 的数据集较大，使得图6（b）中的分数分层更加明显，NFHDDM 算法在综合性能上的优势更加明显。

通过图5和图6对比可以发现，本文提出的NFHDDM算法在综合性能指标上的优势明显，因此可以得出结论，添加四分位距窗口不仅没有增加算法运行的时间和内存消耗，还进一步提高了漂移检测的正确率，减小了漂移检测的延迟度。

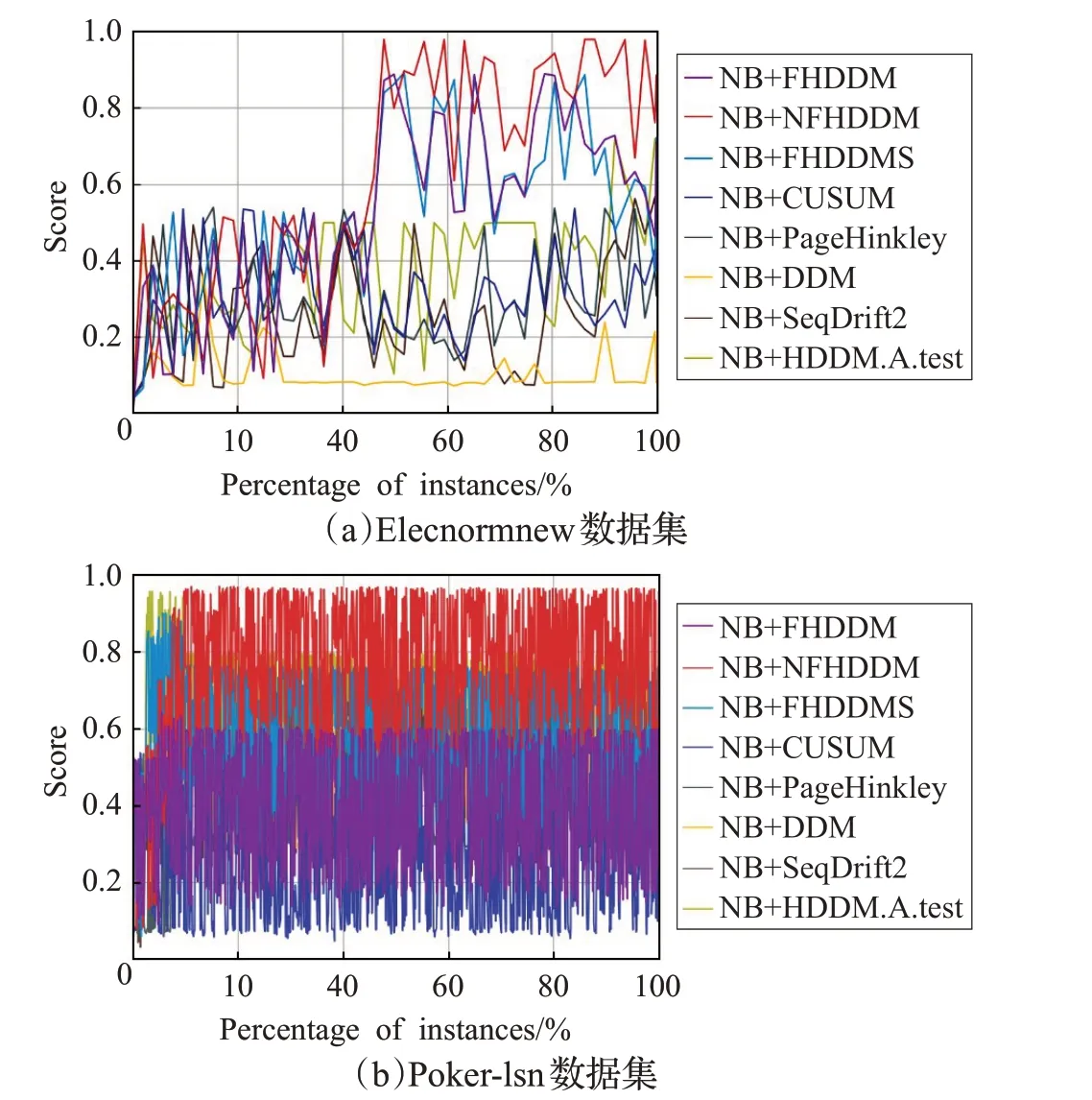
图6 基于真实数据集的综合评估指标分数比较

5 结束语

针对目前主要的概念漂移检测算法中存在的漂移检测延迟度过高的问题，本文提出了基于改进Hoeffding不等式的NFHDDM 算法，该算法使用四分位距的方法选择检测的数据，同时在Hoeffding 不等式中引入概念漂移检测的动态系数，使算法能更好的适应有噪声情况下的真实数据集。实验结果表明，NFHDDM 算法能够在较少的运行时间和较低的内存使用量情况下有效降低漂移检测延迟度，进一步提升隐含概念漂移的数据流分类的正确率。